动态规划解背包问题/C++/Knapsack problem

前言

背包问题是一个经典的算法问题，可以用动态规划，贪心法，分支界限法等方法解决

问题描述：有n个物品，编号1,2,3，、、n，其中第 i 个物品重量为Wi 价值 Vi ，有一个容量为W的背包。

在容量允许范围内，如何选择物品，可以得到最大的价值。（为了简单起见，假设物品的重量 Wi 和价值Vi 都是正数）

 

根据取物品的方式，背包问题又可以被分为三类：

0/1背包问题(0-1 knapsack problem)

这也是最常见的背包问题，对于每个物品，要么取走要么不取走，每个物品只能取一次。

可以用数学表达式表示为：

• maximize   
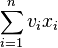
• subject to  

其中xi只能为1 或者0  所以称为背包问题

有界限的背包问题(bounded knapsack problem)

对应于上文，每个物品最多可以取Gi次.也可以不取。用数学表达式描述为：

• maximize 
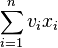
• subject to 

 

注意看xi取值范围。其中的“界限”说的是取的次数上限

无界限背包( unbounded knapsack problem (UKP))

相应的，无界限背包说的就是每个物品取的次数无限了，也就是上文中的xi 可以为任意的正整数。

 

今天主要说的是0、1背包问题，解法是动态规划。当然，对于另外两种问题也会有所介绍。

问题分析：

用动态规划解问题首先要有效的找出子问题，可以通过这个子问题得推得原问题的解，通常子问题的实质是和原问题相同的，只是规模上的缩小，

也就是说子问题和原问题可以有相同的表示形式，问题可通过不断的缩小规模（一般都会有一个界限）能找到子问题的解。

这个问题要求解的是能用背包带走的物品的最大价值。定义 m[i,w] 为：

用第1,、2、3、、i 个物品装入质量<=W的背包的最大价值。

m[i,w]的取值情况分析：

1）  ，背包的质量为w，里面没有物品，所以它的价值为0；

2）   ，背包质量为0，所以里面没法装任何东西， 不论前面的 i 是多少，总价值为0；

对于任意的第 i  个物品，有两种情况，放进背包或者不放。

不要第 i  个物品 如果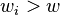 则：

3）    因为第i 个物品的重量大于背包的容量，所以不可放入。

如果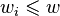. 那么

4）  

对于第 i 个物品，有两种可选择方案：如果放入背包中，那么 m[i,w]=m[i-1,w-wi]+vi　也就是 i 的前一个的最大值加上自己的价值。

如果不要第 i 个物品，那么：m[i,w]=m[i-1,w]。也就是 i 的前一个的最大值。

因为背包问题最后要取得最大的价值，所以就选这两种情况中价值最大的。

 

在这个问题中，定义子问题： m[i,w] 对于每个子问题，都可通过上面的分析求出。通过3），4）可以发现，每一次求取子问题，问题的规模就被缩小。

要么在w 上减小，要么在 i 上减小。最后问题的规模会被缩小为 m[i,0]和m[0,w].而这两个的值都为0，只要逆向思维反推回去，就能逐步得到问题的解。

算法描述

 

 

 

附c++代码：

 c-free 5编译通过

View Code

/*0、1背包问题
一条鱼@博客园 
http://www.cnblogs.com/yanlingyin/ 
2011-12-25 
*/


#include <iostream>
#include<fstream>
#include<algorithm>
#include<vector>

//存储元素的结构 
typedef struct item
{
int weight;
int values;
}item;



using namespace std;
int main()
{
int weight=10;
int itemnum=4;
//int k[10][4];
    

    vector<vector<int> > k(11,vector<int>(5));
    item items[4]={{6,30},{3,14},{4,16},{2,9}};


for(int w=0;w<=weight;w++)
    {
for(int j=0;j<=itemnum;j++)
        {
            k[w][j]=0;    
        }

    }

//输出数组    
    for(int i=0;i<=weight;i++)
    {
for(int j=0;j<=itemnum;j++)
        {
            cout<<k[i][j];
        }
        cout<<"\n";
    }


for(int w=1;w<=weight;w++)
    {
        cout<<"测试\n";  
for(int j=1;j<=itemnum;j++)
        {
if(items[j-1].weight>w)        //物品质量大于背包容量，舍去 
            {
                k[w][j]=k[w][j-1];
            }
else        //对于两种情况选出较大值 
            {
                k[w][j]=max(k[w][j-1],(k[w-items[j-1].weight][j-1]+items[j-1].values));
            }
            cout<<"k["<<w<<"]["<<j<<"]="<<k[w][j]<<"\n";

        }

    }

    cout<<"输出哦了"<<k[weight][itemnum]<<"\n";

for(int i=0;i<=weight;i++)
    {
for(int j=0;j<=itemnum;j++)
        {
            cout<<k[i][j]<<" ";
        }
        cout<<"\n";
    }

}

 

动态规划简单介绍：

动态规划通常用于最优化问题，此类问题可能有很多可行解，每一个解有一个值，而我们希望找出一个具有最优值的解，

动态规划算法设计可分为如下步骤：

1）描述最优解的结构

2）递归定义最优解的值

3）按底向上的方式计算最优解的值

4）由计算出的结果构造一个最优解

动态规划的第一步是描述最优解的结构，如果问题的一个最优解中包含了子问题的最优解，该问题具有最优解结构。当一个子问题

有最优解结构时，提示我们动态规划适用。如本例中的m[i,w]就是一个子问题，里面包含了另一个子问题的最优解：

m[i-1,w],m[i-1,w-1]。解题的过程中把结果记录在数组中，后面的解更具前面的解得出，最后找到问题的解。

 

参考资料： 

http://en.wikipedia.org/wiki/Knapsack_problem

http://www.es.ele.tue.nl/education/5MC10/Solutions/knapsack.pdf

《算法导论》

欢迎转载，请注明出处：http://www.cnblogs.com/yanlingyin/

一条鱼@博客园

2011-12-25

 

 

 

 

转载于:https://www.cnblogs.com/yanlingyin/archive/2011/12/25/Knapsackproblem.html