Internal Sorting Algorithms Part 2/2: Advanced Sorts
目录
概述
在Internal Sorting Algorithms Part 1/2: Elementary Sorts中可以看到,当待排列元素数目不是很大的时候,几种基础的排序算法还是不错的。但是当元素数量增加到十万数量级的时候,插入,选择,希尔,冒泡已经溃不成军,不堪重任了。究其原因,还是因为几种算法的比较或者是数据挪动的次数比较多。下面介绍几种比较快速的内排序。
QuickSort
顾名思义,快速排序,确实快,是在实践中最快的已知排序算法,是一种分治的递归算法。这个算法的思路如下:
- 选择一个枢纽元素
- 小于枢纽元素的都放在其左边,构成数据集合A
- 大于枢纽元素的都放在其右边,构成数据集合B
- 在A中选择一个枢纽元素,重复1,2,3;在B中选择一个枢纽元素,重复1,2,3
- 完成排序
文字生涩,数据结构和算法的讲解最直观的就是画图。
快排可以用挖坑+填坑来很好的解释。
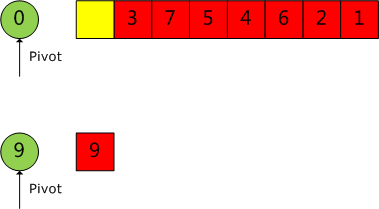
1、 初始元素
2、选择枢纽元素,通常是选取第一个元素,这里是4,但是假如第一个元素是0,那么这样的枢纽元素会产生一个质量超级差的分割,分割后所有元素都在右边。为了优化,惯用的做法是把第一个元素4和中间的元素8交换一下,然后再用第一个元素做枢纽。
此时,i指向第一个元素,j指向最后一个元素,枢纽8被”挖”了出来。留下一个”坑”。
3、j从后往前找,找比8小的元素,填入”坑”中。填进去之后,i往后移一位。j的位置变成新”坑”。
4、i从前往后找,找比8大的元素,填入刚才的新”坑”,填进去之后,j往前移一位。i的位置变成新”坑”。
5、j继续从后往前找,找比8小的元素,移动后j与i相遇,此时i==j,说明这个i==j的位置就是枢纽元素应该在的位置。把8填进去,这样,第一轮的”坑”就填完了。
6、经过第一轮的填”坑”之后,得到如下的数组排列:
7、8左边的元素和8右边的元素形成了两个新的数组,新一轮的挖”坑”填”坑”开始了…
快排的平均时间复杂度是O(NlogN),但是最坏也可能达到O(N^2),为了减少最坏情况发生的概率,通常在选取枢纽元素时,把首元素与中间元素交换。
MergeSort
归并排序是分治算法的另一种应用,也是一种递归算法,并且其时间复杂度最坏为O(NlogN)。归并排序的算法中基本的操作是合并两张已排序的表,因为数据已经是排好序的了,所以若将输出放到第三张表中时则该算法可以通过对输入数据一趟遍历来完成,因此该算法的空间复杂度为O(N)。
还是以图来演示该算法中的并部分。
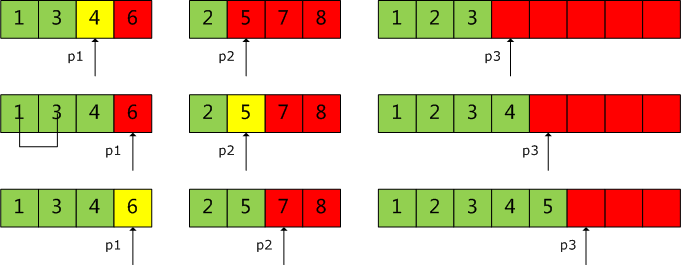
已经排好序的两张表和存储输出的第三张表
1和2比较,1被加入p3中,然后3和2进行比较
2被加入p3中,然后3和5进行比较
3被加入p3,4和5进行比较,一直进行到6和7进行比较
6被加入p3中,p1已经用完
将p2的其余部分拷贝到p3中
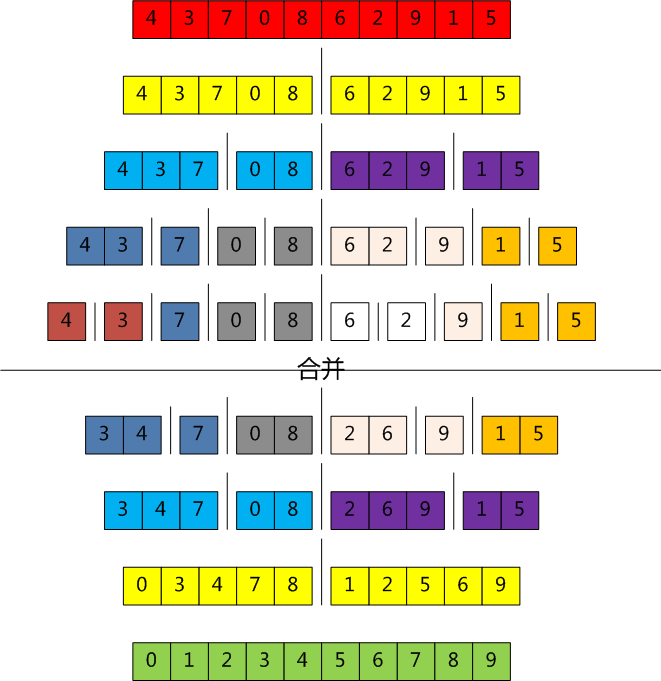
归并算法是将一个大的数组从中间拆成两个数组,再在两个数组的基础上,从各自的中间再拆成两个数组,以此类推,当每个数组中只含有一个元素的时候,停止拆分,肯定有序,此时开始合并,下图展示了递归的过程:
排序完成,简洁高效。
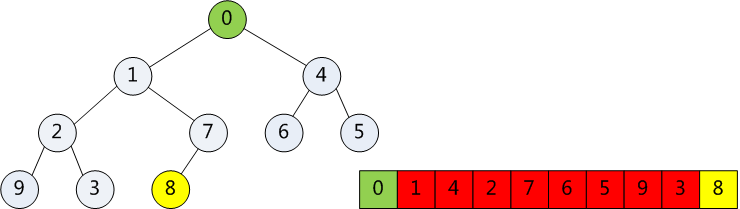
HeapSort
堆排序是一种基于二叉树的排序算法。许多应用程序都需要处理有序的元素,但不一定要求他们全部有序。这种情况下我们就需要一种合适的数据结构,也就是优先队列,支持删除最小(大)元素和插入元素。
我们可以通过插入一列元素然后删掉其中最小(大)的元素,实现堆排序。
有一点需要了解,索引为i的节点的左右孩子分别为2i + 1, 2i + 2(如果有的话)
有兴趣的同学可以证明一下这个结论。
大顶堆: 双亲节点元素值大于所有子节点元素值的堆
小顶堆: 双亲节点元素值小于所有子节点元素值的堆
一般是从索引为N/2(因为大于N/2的肯定是叶子节点了)的节点处从下往上构造堆。
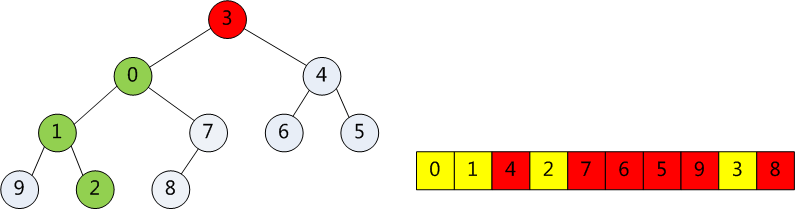
图例如下(构造小顶堆):
N = 10
1、从N/2处取得元素6,没有左右孩子(2 * 5 + 1 > N)
2、前移一位,8,其左孩子为0,没有右孩子。同时8比0大,所以交换一下
3、继续往前移动一位,1,左右孩子分别为9和2,双亲已经满足小顶堆特性,无需移动。
4、继续,4,左右孩子分别为6和5,也满足小顶堆特性,无需移动。
5、往前,7,左右孩子分别为1和0,破坏了小顶堆特性,需要调整,因为0比1小,所以7与右孩子0互换。
6、往前走,到了3,左右孩子分别为0和4,破坏了小顶堆特性,0比4小,所以3和0互换。互换后3的左右孩子为1和7,也不能满足小顶堆,3和1互换。互换后,3的左右孩子为9和2,同样需要调整,3和2互换。
7、经过一轮调整后生成的小顶堆如下所示:
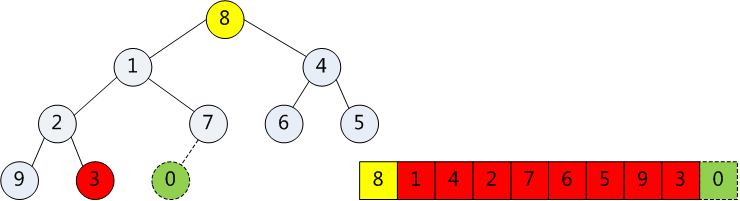
8、如上图所示,此时树根0是最小的,8的索引是最大的,把0和8互换,并将数组的长度较少1(把互换后的0排除在外),树又不满足小顶堆的特性了,需要再次调整。
9、因为数组长度减少了1,所以3的位置是最后一个元素,把第二轮构造的小顶堆的根与此位置的元素交换,以此类推,就得到了逆序排列的元素表,完成排序。
一个典型的应用就是需要选取N个元素中第K大的元素。不需要排列所有元素,即可知晓。
代码实现
原理弄清楚了,代码实现起来只不过是一项翻译的工作。
// Sort.java
package com.stephen.sortalgorithms;
public interface Sort {
void sort(int[] array);
}
// SortUtils.java
package com.stephen.sortalgorithms;
public class SortUtils {
private static void swap(int[] array, int left, int right) {
int temp = array[left];
array[left] = array[right];
array[right] = temp;
}
// ... 省略了part1中的几种基础排序算法
/**
* 快速排序
*/
public static class QuickSort implements Sort {
@Override
public void sort(int[] array) {
quickSort(array, 0, array.length - 1);
}
private void quickSort(int[] array, int left, int right) {
if(left > right || array == null) return;
int i = left, j = right;
swap(array, left, (left + right) / 2); // 交换第一个元素和中间元素,优化一下
int pivot = array[left];
while(i < j) {
while(array[j] > pivot && i < j) --j; // 从后往前找,找到第一个比pivot小的元素
if(i < j) array[i++] = array[j];
while(array[i] < pivot && i < j) ++i; // 从前往后找,找到第一个比pivot大的元素
if(i < j) array[j--] = array[i];
}
array[i] = pivot; // 把pivot放在它应该在的位置
quickSort(array, left, i - 1);
quickSort(array, i + 1, right);
}
}
/**
* 归并排序
*/
public static class MergeSort implements Sort {
@Override
public void sort(int[] array) {
int[] temparray = new int[array.length]; // 一定要在外面创建好,不要进去创建,不然效率会很低
mergeSort(array, temparray, 0, array.length - 1);
}
private void mergeSort(int[] array, int[] temparray, int left, int right) {
if(left >= right) return;
int mid = (left + right) >> 1;
mergeSort(array, temparray, left, mid);
mergeSort(array, temparray, mid + 1, right);
merge(array, temparray, left, mid, right);
}
private void merge(int[] array, int[] temparray, int left, int mid, int right) {
int i = left, j = mid + 1, k = 0;
while(i <= mid && j <= right) {
if(array[i] <= array[j]) temparray[k++] = array[i++];
if(array[i] > array[j]) temparray[k++] = array[j++];
}
while(i <= mid) temparray[k++] = array[i++];
while(j <= right) temparray[k++] = array[j++];
for(int index = 0; index < right - left + 1; ++index) {
array[left + index] = temparray[index];
}
}
}
/**
* 堆排序
*/
public static class HeapSort implements Sort {
@Override
public void sort(int[] array) {
for(int i = array.length / 2; i >= 0; --i) { // 从N/2开始
heapSort(array, i, array.length);
}
for(int i = array.length - 1; i > 0; --i) { // 从N-1开始
swap(array, 0, i);
heapSort(array, 0, i - 1);
}
}
// 有兴趣的同学可以试试递归
// 构造大顶堆
private void heapSort(int[] array, int parent, int length) {
int child;
int tmp;
for(tmp = array[parent]; (child = 2 * parent + 1) < length; parent = child) {
// 找到比较大的孩子
if(child != length - 1 && array[child + 1] > array[child]) child++;
if(tmp < array[child]) array[parent] = array[child]; // parent处存入"大"孩子的值
else break;
}
array[parent] = tmp;
}
}
}
// SortTest.java
package com.stephen.sortalgorithms;
import java.lang.reflect.InvocationHandler;
import java.lang.reflect.Method;
import java.lang.reflect.Proxy;
import java.util.Arrays;
import java.util.Date;
public class SortTest{
private static final int SIZE = 10000000;
private static int[] array;
static {
array = new int[SIZE];
for(int i = 0; i < SIZE; ++i) {
array[i] = (int)(Math.random() * SIZE);
}
}
public static void main(String[] args) {
benchmark();
}
public static void benchmark() {
int[] arraycopy = null;
Sort[] sorts = {
new SortUtils.InsertSort(),
new SortUtils.SelectSort(),
new SortUtils.BubbleSort(),
new SortUtils.ShellSort(),
new SortUtils.QuickSort(),
new SortUtils.MergeSort(),
new SortUtils.HeapSort(),
};
for(Sort sort: sorts) {
InvocationHandler handler=new SortHandler(sort);
Sort proxy=(Sort)Proxy.newProxyInstance(
sort.getClass().getClassLoader(),
sort.getClass().getInterfaces(),
handler);
arraycopy = Arrays.copyOf(array, SIZE);
proxy.sort(arraycopy);
}
}
public static void printarray(int[] arraycopy) {
for(int i: arraycopy) System.out.println(i);
}
}
class SortHandler implements InvocationHandler{
private Object target;
public SortHandler(Object target) {
super();
this.target = target;
}
public Object invoke(Object proxy, Method method, Object[] args) throws Throwable {
long start = new Date().getTime();
Object result=method.invoke(target, args);
long end = new Date().getTime();
System.out.println(String.format("%-10s %s: %d", target.getClass().getSimpleName(),"consuming", (end - start)));
return result;
}
}
Summary
以上各算法(含part1的排序算法)在同一台机器上的运行时间以及对应的元素数目如下所示:
/*
* Time consuming of each sort, in millisecond
*/
/*
* 10,000 random numbers
*/
InsertSort consuming: 58
SelectSort consuming: 84
BubbleSort consuming: 247
ShellSort consuming: 32
QuickSort consuming: 2
MergeSort consuming: 3
HeapSort consuming: 4
/*
* 100,000 random numbers
*/
InsertSort consuming: 5053
SelectSort consuming: 8218
BubbleSort consuming: 22564
ShellSort consuming: 2965
QuickSort consuming: 13
MergeSort consuming: 20
HeapSort consuming: 13
/*
* 500,000 random numbers, unbearable
*/
InsertSort consuming: 134790
SelectSort consuming: 214202
BubbleSort consuming: 582737
ShellSort consuming: 91378
QuickSort consuming: 89
MergeSort consuming: 101
HeapSort consuming: 106
/*
* 1,000,000 random numbers
*/
QuickSort consuming: 122
MergeSort consuming: 212
HeapSort consuming: 319
/*
* 10,000,000 random numbers
*/
QuickSort consuming: 1379
MergeSort consuming: 2372
HeapSort consuming: 5250可以看到即使元素个数在千万级别,这三种排序算法依然很给力,而最给力的当属快速排序!名不虚传!
以下为七种排序算法的总结
| algorithm | stable? | in place? | running time | extra space |
|---|---|---|---|---|
| insertsort | yes | yes | O(N^2) | 1 |
| shellsort | no | yes | O(N^7/6?) | 1 |
| selectsort | no | yes | O(N^2) | 1 |
| bubblesort | yes | yes | O(N^2) | 1 |
| quicksort | no | yes | Nlog(N) | logN |
| mergesort | yes | no | Nlog(N) | N |
| heapsort | no | yes | Nlog(N) | 1 |





































 5382
5382

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








