最近几天在刷蓝桥杯往年的真题, 发现数据结构方面的考察较少, 许多问题可以通过递归解决. 还有两套往年试题没有刷, 先就已经刷的题目总结一下.
几种常见的递归题目
1. 类型一
2. 类型二
3. 类型三
4. 类型四
5. 其他类型
类型一
描述: 这类递归题目的原型是让一个字符串全排列, 比如说现在有字符串"abc", 它还可以有"acb", "bac", "bca", "cab", "cba"等排列方式. 通过全排列的方式可以得到全部可能的结果, 然后再从可能的结果中选出符合要求的结果.
这种题目一般有两个考察重点, 一个是全排列怎么写,(这个代码套路是固定的)
另外一个就是判断某个排列是否符合要求, 在判断这一步能考很多细节
例题: 带分数
- 100 可以表示为带分数的形式:100 = 3 + 69258 / 714
- 还可以表示为:100 = 82 + 3546 / 197
- 注意特征带分数中,数字1~9分别出现且只出现一次(不包含0)。
- 类似这样的带分数,100 有 11 种表示法。
题目要求:
从标准输入读入一个正整数N (N<1000*1000)
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
例如:
用户输入:
100
程序输出:
11
再例如:
用户输入:
105
程序输出:
6题目分析:
- 这是一道典型非常典型的题目. 1~9个数字每个自能出现一次, 为了求出所有结果, 我们必须先求出所有的数字组合, 然后再判断每个数字组合是否能凑出这样的带分数.
public class DaiFenShu {
public static int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
public static int n;
public static int res = 0;//记录结果
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
process(0);//全排列
System.out.println(res);
}
public static void process(int index){
if(index == arr.length){
check();//得出一种排列, 判断排列是否符合要求.
return;
}
for(int i = index; i < arr.length; i++){
swap(i, index);
process(index + 1);
swap(i, index);
}
}
public static void check(){
for(int i = 0; i < arr.length - 3; i++){
for(int j = i + 1; j < arr.length - 2; j++){
int jiaShu = getNum(0, i);//带分数种的加数
int fenZi = getNum(i + 1, j);//分子
int fenMu = getNum(j + 1, arr.length - 1);//分母
if(fenZi % fenMu == 0 && jiaShu + fenZi / fenMu == n){//分子要能整除分母(也可以用float保存3种数, 就不用判断整除)
res++;
}
}
}
}
public static int getNum(int i, int j){
int num = 0;
int system = 1;//用于算10的次方的基数, 如果用系统Math.pow()算10次方的话会慢很多.
for(int n = j; n >= i; n--){
num += arr[j--] * system;
system *= 10;
}
return num;
}
public static void swap(int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
类型二
描述: 我曾经在学习汉诺塔问题的时候, 被那简单的几行代码惊艳到. 这种类型的递归我擅自给他命名为状态转移型递归. 类似这种套路的递归在很多问题中也能用到, 比如下面的例题, 两人博弈, 大家的操作都是一样的, 就是状态发生了变化.
例题: 取球博弈
- 两个人玩取球的游戏。
- 一共有N个球,每人轮流取球,每次可取集合{n1,n2,n3}中的任何一个数目。
- 如果无法继续取球,则游戏结束。
- 此时,持有奇数个球的一方获胜。
- 如果两人都是奇数,则为平局。
- 假设双方都采用最聪明的取法,
- 第一个取球的人一定能赢吗?
- 试编程解决这个问题。
- 输入格式:
- 第一行3个正整数n1 n2 n3,空格分开,表示每次可取的数目 (0<n1,n2,n3<100)
- 第二行5个正整数x1 x2 ... x5,空格分开,表示5局的初始球数(0<xi<1000)
- 输出格式:
- 一行5个字符,空格分开。分别表示每局先取球的人能否获胜。
- 能获胜则输出+,
- 次之,如有办法逼平对手,输出0,
- 无论如何都会输,则输出-
例如,输入:
1 2 3
1 2 3 4 5
程序应该输出:
+ 0 + 0 -
再例如,输入:
1 4 5
10 11 12 13 15
程序应该输出:
0 - 0 + +
再例如,输入:
2 3 5
7 8 9 10 11
程序应该输出:
+ 0 0 0 0
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms思路
- 首先要明确每一局的情况, 假设一局有x个球, 取球情况的数组为n.
- 在每一局中, 某一方取球都会根据取球情况数组进行试探, 如上图.
- 在每次递归中, 需要的参数有当前剩下的球, 我摸的球数, 对手摸的球数.
- 如何才能判断一局的胜负? 在所有情况中, 只要对手输过, 结果就是赢; 如果对手没输过, 但是平过, 结果就是平; 否则, 结果就是输. (因为题目条件: 双方都采取最聪明的办法)
- 最大的难点在于在于递归的过程中, 不是每次都是我摸, 而是我摸一次, 对手摸一次, 这里恰好就是这种类型递归的魅力所在.
- 具体落实到代码中
public class QuQiuBoYi {
public static int[] n = new int[3];
public static int[] m = new int[5];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for(int i = 0; i < 3; i++){
n[i] = sc.nextInt();
}
Arrays.sort(n);
for(int i = 0; i < 5; i++){
m[i] = sc.nextInt();
char res = process(m[i], 0, 0);//每输入一局的球数, 就计算一局
System.out.print(res + " ");
}
}
public static char process(int num, int me, int you){
if(num < n[0]){//没球可摸,进行结算
if((me & 1) != 0 && (you & 1) == 0){//我奇数, 对手偶数, 赢
return '+';
}else if((me & 1) == 0 && (you & 1) != 0){//我偶数, 对手奇数, 输
return '-';
}else{
return '0';//平
}
}
boolean draw = false;
for(int i = 0; i < 3; i++){
if(num >= n[i]){
//重点!假设当前这轮是我摸球, 在我摸完球me+n[i]后, 就到对手摸, me和you的位置转换, 设定中间的参数是摸球的一方
char res = process(num - n[i], you, me + n[i]);
if(res == '-'){//由于下一轮是对手摸球, 如果他输了
return '+';//我就赢了
}else if(res == '0'){//如果有平局, 要记录下来
draw = true;
}
}
}
return draw ? '0' : '-';
}
}优化
- 作为编程大题, 如果不优化是过不了极端的数据样本的.
- 这题可以用数组记录重复出现的情况, 进行记忆型递归, 用空间换时间.
- 问题来了: me和you是不断交换的, 怎样才算是一种情况?
- 在base case中, 最后决定输赢的, 不是你我手上有多少个球, 而是你我的球数的奇偶情况, 所以我们把每一种情况记录为: 剩余的球数和双方球数的奇偶情况.
public class Nine {
public static int[] n = new int[3];
public static int[] m = new int[5];
public static char[][][] cache = new char[1000][2][2];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for(int i = 0; i < 3; i++){
n[i] = sc.nextInt();
}
Arrays.sort(n);
for(int i = 0; i < 5; i++){
m[i] = sc.nextInt();
char res = process(m[i], 0, 0);
System.out.print(res + " ");
}
}
public static char process(int num, int me, int you){
if(num < n[0]){
if((me & 1) != 0 && (you & 1) == 0){
return '+';
}else if((me & 1) == 0 && (you & 1) != 0){
return '-';
}else{
return '0';//平
}
}
if(cache[num][me][you] != '\0'){
return cache[num][me][you];
}
boolean draw = false;
for(int i = 0; i < 3; i++){
if(num >= n[i]){
char res = process(num - n[i], you, ((me + n[i]) & 1) == 0 ? 0 : 1);//只记录奇偶情况
if(res == '-'){
cache[num][me][you] = '+';
return '+';
}else if(res == '0'){
draw = true;
}
}
}
if(draw){
cache[num][me][you] = '0';
return '0';
}else{
cache[num][me][you] = '-';
return '-';
}
}
}
类型三
描述: 第二种递归, 这种题目一般都和走矩阵和走格子有关, 每一层递归里面都要进行操作, 每次递归都会影响到最后的结果. 每一次递归, 根据参数可以确定为一种状态, 如果固定的状态对应固定的结果, 称之为无后效性递归, 这样的递归就可以通过画表格, 填表格的方式改成动态规划. 如果不改成动态规划的话, 可以用数组记录下每个状态对应的结果, 如果再次来到这种状态, 可以直接查表得出结果, 进行记忆型递归.
例题: 地宫寻宝
- X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
- 地宫的入口在左上角,出口在右下角。
- 小明被带到地宫的入口,国王要求他只能向右或向下行走。
- 走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
- 当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
- 请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
例如,输入:
2 2 2
1 2
2 1
程序应该输出:
2
再例如,输入:
2 3 2
1 2 3
2 1 5
程序应该输出:
14
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms解题思路:
- 每来到一个格子, 先判断能不能拿起宝贝. 如果能不能拿起来, 就有两种选择, 往右或下走; 如果能拿起来, 就有4种选择, 往右或下走, 并选择是否拿起宝贝. 所以在递归的过程中除了传递位置的参数, 还要维护一个当前宝贝的最大值, 和一个已经拿了多少个宝贝的变量. 为了能达到时间和空间的要求, 必须使用记忆数组优化.
public class DiGongXunBao {
public static int n;
public static int m;
public static int k;
public static int mod = 1000000007;
public static int[][] arr = new int[50][50];
public static int[][][][] dp = new int[50][50][15][15];
public static void main(String[] args) {
initDp();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
arr[i][j] = sc.nextInt();
}
}
System.out.println(process(0, 0, -1, 0));
}
public static int process(int x, int y, int max, int cur){
if(dp[x][y][max + 1][cur] != -1){
return dp[x][y][max + 1][cur];
}
if(x == n - 1 && y == m - 1){
if(cur == k || (arr[x][y] > max && cur == k - 1)){
return 1;
}
}
if(x >= n || y >= m || cur > k){
return 0;
}
int value = arr[x][y];
int res = 0;
if(value > max){
res += process(x + 1, y, value, cur + 1);
res %= mod;
res += process(x, y + 1, value, cur + 1);
res %= mod;
}
res += process(x + 1, y, max, cur);
res %= mod;
res += process(x, y + 1, max, cur);
res %= mod;
dp[x][y][max + 1][cur] = res;
return dp[x][y][max + 1][cur];
}
public static void initDp(){
for(int a = 0; a < 50; a++){
for(int b = 0; b < 50; b++){
for(int c = 0; c < 15; c++){
for(int d = 0; d < 15; d++){
dp[a][b][c][d] = -1;
}
}
}
}
}
}
类型四
描述: 每次递归时的操作受到之前递归的限制. 典型的是八皇后问题. 每次递归填的数会限制到下一次递归填的数. 这种问题要注意一个关键的因素是要进行回溯. 因为如果不回溯的话下一步的递归就不能遍历所有可能性. 看具体例子.
例题: 方格填数
- 如下的10个格子
+--+--+--+
| | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | |
+--+--+--+- 填入0~9的数字。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻) - 一共有多少种可能的填数方案?
- 请填写表示方案数目的整数。
解题思路:
- 每次递归填一个数要考虑连续的数不能相邻, 也就是要考虑一个数周围的8个格子的数都不能与其相邻. 如果直接在原图的不规则矩阵中操作会非常不方便, 可以通过扩充矩阵, 让每个格子周围都有8个格子.
扩充成5*6的矩阵
+--+--+--+--+--+--+
|xx|xx|xx|xx|xx|xx|
+--+--+--+--+--+--+
|xx|xx| | | |xx|
+--+--+--+--+--+--+
|xx| | | | |xx|
+--+--+--+--+--+--+
|xx| | | |xx|xx|
+--+--+--+--+--+--+
|xx|xx|xx|xx|xx|xx|
+--+--+--+--+--+--+public class FangGeTianShu {
public static int res = 0;
public static int[] a = new int[10];
public static int[][] p = new int[5][6];
public static void main(String[] args) {
initP();
process(1, 2);
System.out.println(res);
}
public static void process(int x, int y){
if(x == 3 && y == 4){
res++;
return;
}
for(int i = 0; i <= 9; i++){
if(canFill(i, x, y) && a[i] == 0){
p[x][y] = i;
a[i] = 1;
if(y == 4){
process(x + 1, 1);
}else{
process(x, y + 1);
}
a[i] = 0;
p[x][y] = -10;
}
}
}
public static boolean canFill(int num, int x, int y){
for(int i = -1; i <= 1; i++){
for(int j = -1; j <= 1; j++){
if(i == 0 && j == 0) continue;
if(Math.abs(p[x + i][y + j] - num) <= 1){
return false;
}
}
}
return true;
}
public static void initP(){
for(int i = 0; i < 5; i++){
for(int j = 0; j < 6; j++){
p[i][j] = -10;
}
}
}
}
其他类型
描述: 其他类型递归这里暂且只描述一种, 它令我印象深刻. 在一个大问题中要拆分成许多个小问题, 大问题的答案要通过小问题的答案生成. 对应在递归就是父递归要得出结果必须先通过子递归得出结果.
例题: 生命之树
- 在X森林里,上帝创建了生命之树。
- 他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b} 使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。 - 在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。 - 经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算,他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。
「输入格式」
第一行一个整数 n 表示这棵树有 n 个节点。
第二行 n 个整数,依次表示每个节点的评分。
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。由于这是一棵树,所以是不存在环的。
「输出格式」
输出一行一个数,表示上帝给这棵树的分数。
「样例输入」
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
「样例输出」
8
「数据范围」
对于 30% 的数据,n <= 10
对于 100% 的数据,0 < n <= 10^5, 每个节点的评分的绝对值不超过 10^6 。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms思路
- 题目的意思是有一颗连通的树, 任意连通的点都可以构成一个点集, 现在的问题是如何求得一个和最大的点集.
- 先根据样例输入画图, 画成一棵树的样子以便分析.
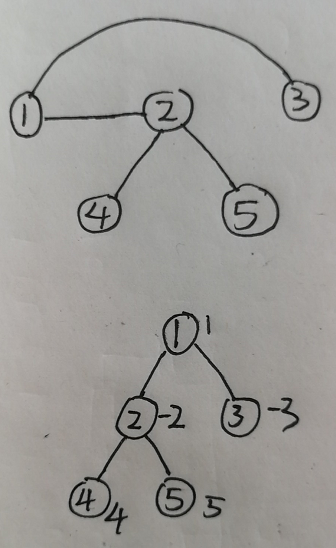
- 画树的时候选取根结点是任意的.
- 我们以一棵树分析如何求最大和点集, 假设对结点2进行分析.
- 以结点2为源头, 向子结点方向扩充子集的范围, 最开始子集里只有结点2, 也就是-2.
- 遍历到左孩子4, 如果以该节点为源的子集的值大于0, 那么子集就加上这个结点, 因为这样会使子集的和增大. 于是子集的和变成
-2 + 4 = 2. - 然后继续遍历孩子结点, 把结点5也加入进来, 最终子集的和变成
2 + 5 = 7. - 这样便确认了以2为起点的点集的最大和.
- 通过这一逻辑, 可以推出递归函数.
public class ShengMingZhiShu {
public static List<Integer>[] rel;
public static int[] arr;
public static void main(String[] args) {
//处理输入
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
arr = new int[n + 1];
rel = new ArrayList[n + 1];
initRelArr();
for(int i = 1; i < arr.length; i++){
arr[i] = sc.nextInt();
}
for(int i = 0; i < n - 1; i++){
int a = sc.nextInt();
int b = sc.nextInt();
rel[a].add(b);
rel[b].add(a);
}
process(1, 0);
int max = Integer.MIN_VALUE;
for(int i = 1; i < arr.length; i++){
max = Math.max(max, arr[i]);
}
System.out.println(max);
}
public static void process(int cur, int father){
int max = arr[cur];//拿到当前结点的值作为初始值.
for(int i = 0; i < rel[cur].size(); i++){//遍历孩子点集
int son = rel[cur].get(i);
if(son == father) continue;//防止孩子点集中包含当前结点
process(son, cur);//计算孩子点集的最大和
if(arr[son] > 0){
max += arr[son];
}
}
arr[cur] = max;//计算完以当前结点为源的点集的最大和, 保存进数组.
}
public static void initRelArr(){
for(int i = 0; i < rel.length; i++){
rel[i] = new ArrayList<Integer>();
}
}
}
总结
- 蓝桥杯题目中很多题目能用递归解决, 在递归题目中相当一部分题目是有规律的, 在规律之下, 不同的题目又有不同的细节需要处理, 挺锻炼人的. 当然也有的递归题目不能用常规套路, 需要对具体题目具体分析. 希望自己能在比赛中做出更多题目.























 4407
4407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








