【JZOJ4815】【NOIP2016提高A组五校联考4】ksum

题目描述

输入

输出

样例输入

3 4
1 3 4

样例输出

8 7 4 4

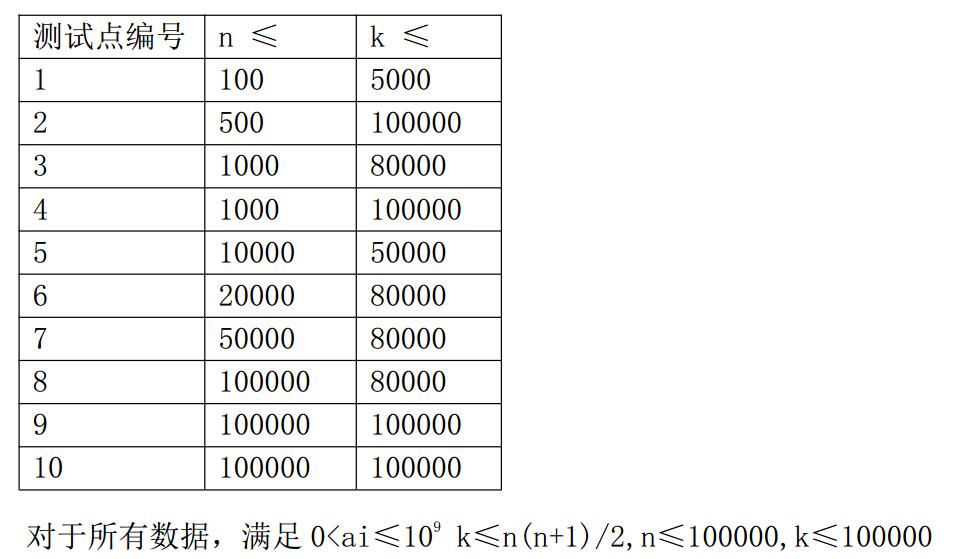
数据范围

样例解释

解法

二分做法

考虑到可以二分第k大的值mid，如果比mid大的区间和数小于或等于mid，那么mid就合法。
找一个合法的最小mid就是我们要找的mid。

---

询问有多少个区间大于或等于mid可以使用dfs，从[1,n]开始；
设当前dfs到[l,r]，如果当前区间合法，就可以推到[l,r-1]和[l+1,r]。
否则直接退出。

---

时间复杂度为O(log(maxa)∗k)。

堆做法

先把所有[1,i]加入堆中。
操作k次：
1.取出堆中最大的一个区间并输出。
2.设这个区间为[l,r]，如果l<r，那么把[l+1,r]加入堆中。

---

正确性：
由于可以[l,r]一定大于[l+1,r]，所以一开始堆外元素一定没有比任何堆中元素更大的。

---

时间复杂度为O(log(maxa)∗k)。

代码

#include<iostream>
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#define ll long long
#define ln(x,y) ll(log(x)/log(y))
#define sqr(x) ((x)*(x))
using namespace std;
const char* fin="ksum.in";
const char* fout="ksum.out";
const ll inf=0x7fffffff;
const ll maxn=100007;
ll n,m,i,j,k,l,r,mid,mmid,sum=0,num,head,tail;
ll a[maxn],c[maxn*2],b[maxn*2][2];
bool ansflag;
void add(ll l,ll r){
    b[++tail][0]=l;
    b[tail][1]=r;
}
void dfs(ll l,ll r,ll limit){
    head=0;
    tail=0;
    add(l,r);
    while (head++<tail){
        ll l=b[head][0],r=b[head][1];
        if (a[r]-a[l-1]>=limit){
            num++;
            if (ansflag) c[++c[0]]=a[r]-a[l-1];
        }else continue;
        if (!ansflag && num>m) continue;
        if (l==r) continue;
        if (r==n) add(l+1,r);
        if (!ansflag && num>m) continue;
        add(l,r-1);
    }
}
bool judge(ll x){
    num=0;
    dfs(1,n,x);
    if (num>=m) return true;
    else return false;
}
int main(){
    freopen(fin,"r",stdin);
    freopen(fout,"w",stdout);
    scanf("%d%d",&n,&m);
    if (m==0) return 0;
    for (i=1;i<=n;i++){
        scanf("%d",&a[i]);
        a[i]+=a[i-1];
    }
    l=1;
    r=a[n];
    while (l<r-1){
        mid=(l+r)/2;
        if (judge(mid)) l=mid;
        else r=mid;
    }
    if (!judge(l)) l=r;
    ansflag=true,num=0,dfs(1,n,l);
    sort(c+1,c+c[0]+1);
    for (i=c[0];i>c[0]-m;i--) printf("%lld ",c[i]);
    return 0;
}

启发

把问题想复杂了，不需要二分甚至三分。
好好利用[l,r]>max([l+1,r],[l,r−1])这个性质即可解题。

转载于:https://www.cnblogs.com/hiweibolu/p/6714874.html