题目描述
输入
输出
样例输入
2x^2+3x+1
样例输出
4x+3
数据范围
样例解释
求导的意思:
多项式是由若干个单项式构成的
单项式的一般形式是ax^b,其中ab都是常数,x是自变量
对于单项式ax^b求导,结果就是(ab)x^(b-1)
对于多项式求导,就是把构成它的所有单项式分别求导之后相加
特别地,对于ax^0,即对常数a求导,结果是0
解法
模拟即可;
注意细节:
1.系数可为负;
2.处理+-号
3.当系数为1时,系数省略;
4.特别地:输入2+2x^2,输出2x。
代码
#include<iostream>
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#define ll long long
#define ln(x,y) ll(log(x)/log(y))
#define sqr(x) ((x)*(x))
using namespace std;
const char* fin="equation.in";
const char* fout="equation.out";
const ll inf=0x7fffffff;
const ll maxn=1007;
char a[maxn],ch;
bool bz=false,cz=false;
void poke(){
ll i=1,j=0,k=0;
if (ch=='-') i=-1;
ch=getchar();
if (ch=='-') i=-1;
while (ch>='0' && ch<='9') k=k*10+ch-'0',ch=getchar();
if (ch!='x') {
if (ch=='+') bz=true;
return;
}
if (k==0) k=1;
ch=getchar();
if (ch!='^'){
if (bz) printf("+"),bz=false;
k=i*k;
printf("%lld",k);
if (ch=='+') bz=true;
cz=true;
return;
}
ch=getchar();
while (ch>='0' && ch<='9') j=j*10+ch-'0',ch=getchar();
k*=j*i;
j--;
if (bz) {
if (cz) printf("+");
bz=false;
}
printf("%lldx",k);
if (j>1) printf("^%lld",j);
if (ch=='+') bz=true;
cz=true;
}
int main(){
freopen(fin,"r",stdin);
freopen(fout,"w",stdout);
while (1){
poke();
if (ch!='+' && ch!='-') break;
}
if (!cz) printf("0");
return 0;
}启发
多出特殊的数据,多考虑细节。
像这种模拟题看起来简单,但细节不可忽视。









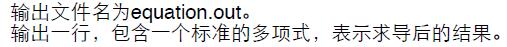
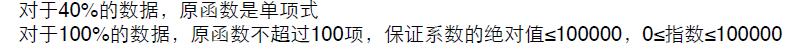
















 336
336

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








