小清新数论题泛做

1、bzoj3481 DZY Loves Math III

求\(xy \equiv Q \pmod {P}\)的解的组数。以乘积形式输入\(P,Q\)。
题解
一来直接把P拆质因子转成多个方程最后求乘积。
现在考虑\(xy \equiv Q \pmod {pi^{ai}}\)的解的组数。
设\(p=pi^{ai}, Q=pi^{bi}\)
假设枚举x
则答案为 sigma gcd(x,p) 其中[gcd(x,p) | q]
改成枚举d=gcd(x,p)
或者说枚举gcd有几个pi因子
则答案为 sigma d* (sigma x: [gcd(x,p/d) == 1]) 其中d | gcd(p,Q)
这是因为你x含有的pi因子不能比d多，所以gcd(x,p/d) == 1
这个是欧拉函数
答案为 \(\sum_{d | gcd(p,Q)} d*φ(p/d)\)
枚举i从0至\(min(a_i,b_i)\)，算一下就行，要用公式把\(φ(p^a)\)拆开
\(φ(p^a)=p^a*(p-1)/p (a>0)\)
注意指数为0特判即可
Q等于0也要特判
(注意)一个小trick：\(gcd(i,a)==b \iff gcd(i/a,b/a)==1\)

2、无能为力

数据范围\(10^9\)
题解
比较毒瘤
细节超多
（1）发现i=0时原式值为1，所以先不考虑0最后加上
（2）按照套路，大胆猜测斐波那契循环节为\(P-1\)要不然没法做。。。
（3）拆质因子发现\(P-1=961749330=2 * 3 * 5 * 17 * 29 * 65027\)
（4）发现枚举\(i\)没有前途，于是枚举 \(gcd(i,n)=d\)，然后发现$ \dbinom{n}{d} $ 和 \(x^d\) 直接算即可
（5）考虑求满足\(gcd(i,n)=d\)的\(y^i\)之和
\(gcd(i,n)==d \iff gcd(i/d,n/d)==1\)
即求满足\(gcd(i/d,n/d)==1\)的\(y^i\)之和
对\(n/d\)的质因子暴力容斥
设枚举到\(n/d\)的一个因子为\(U\)
则贡献为$ \sum_{k=1}^{N/U} y^{Uk} $
这个式子的值可以分治+快速幂解决

（6）然后发现\(5\)在模\(961749331\)意义下有二次剩余，求Fib数列直接做就可以了

3、Function

数据范围\(10^{18}\)
题解
推式子题
上来先打表
扔进OEIS
发现一个很不显然的规律
$f(n)= \sum_{i^2 | n} {\frac{n}{i^2}} $
于是我们愉快的枚举\(i^2\)即可
这样枚举范围就变成\(10^9\)
可以推出\(Ans=\sum_{i=1}^{\sqrt{n}} \frac{\left \lfloor \frac{n}{i^2} \right \rfloor * (\left \lfloor \frac{n}{i^2} \right \rfloor + 1)}{2}\)
数论分块即可。
注意本题卡\(cmath\)的\(sqrt()\)精度
传入参数时转成\(long double\)可以解决
速度垫底不知道为什么QwQ

4、Function（2）

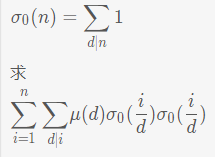
数据范围\(10^9\)，多测。
题解
推式子题
上来先打表
发现一个不是很显然的规律
设\(d(n)\)表示约数个数函数：
则\(\sum_{i|n} {μ(i)d(n/i)^2} = d(n^2)\)
数据范围\(10^9\)？
我会暴力！
分块打表即可，由于30kb大小限制，块大小顶多设\(500000\)
交上去发现\(TLE\)
略加优化：块内的某个位置从两端逼近，比如\(F(999888)\)由\(F(1000000)\)来计算，而\(F(2002333)\)由\(F(2000000)\)来计算
常数减小一倍，就通过了。

5、Ceil it！

数据范围 N<=\(10^{18}\)

题解（纯图片）

6、Road

题意及数据范围：
求\(\sum_{i=1}^N G^i*i^M,N\le 10^9,M\le 50,G\)为\(A*A\)的矩阵,\(A\le 50\)。

题解：
\(tag\)：分治，倍增，二项式定理，矩阵乘法
因为二项式定理同样适用于矩阵，矩阵的乘法、加法也可以直接运算，因此我们可以把\(G\)直接当常数做。
设\(F(n,m)\)表示\(\sum_{i=1}^n G^i*i^m\)
答案为\(F(N,M)\)
直接递推求\(F(N,M)\)复杂度显然不可接受。
考虑快速幂形式的倍增：
\(F(2n,m)\)
\(=\sum_{i=1}^{2n} G^i*i^m\)
\(=\sum_{i=1}^n G^i*i^m + G^n\sum_{i=1}^n G^i*(i+n)^m\)
\(=F(n,m)+G^n\sum_{i=1}^n G^i\sum_{j=0}^m \dbinom{m}{j} i^j n^{m-j}\)
\(=F(n,m)+G^n\sum_{j=0}^m \dbinom{m}{j} n^{m-j}\sum_{i=1}^n G^ii^j\)
\(=F(n,m)+G^n\sum_{j=0}^m \dbinom{m}{j} n^{m-j} F(n,j)\)

对\(i\)维护\(F(i,0...m)\)
然后做快速幂
复杂度\(O(MA^3logN)\)

7、Fib

求第\(K\)大的满足条件的自然数\(N\)：
(1)N在Fibnacci数列中。
(2)N是完全平方数。
若不存在输出\(-1\)
\(K\le 10^9\)

题解
只有\(1,1,144\)符合要求。

8、求\(\dbinom{n}{p} \pmod{p}\)

\(p\)是质数，\(3\le p\le n\le 10^{1000}\)

题解
手玩Lucas
答案即\(\left \lfloor \frac{n}{p} \right \rfloor\)
高精度除法膜法

9、最大公约数

求\(GCD(\dbinom{2N}{1},\dbinom{2N}{3},...,\dbinom{2N}{2N-1})\)，答案对\(1000000007\)取模
\(N\le 10^{100000}\)

题解
\(lowbit(2N)\)

10、简单数论题

题目描述：
给三个两两互质的数 \(a,b,c\)，以及另一个数 \(m\), 现在他希望找到三个\((0,m)\)内的整数\(x,y,z\)，
使得\(x^a+y^b=z^c \pmod{m}\)。\(10^5\)组数据，\(a,b,c,m\le 10^9\)。

Sol:
用\(2\)的方幂构造答案即可。
具体的，
构造\(p\times a=q\times b=t\)，
这样得到\((2^p)^a+(2^q)^b=2\times 2^t=2^{t+1}\)，
只要用\(exgcd\)搞出\(2^{t+1}=(2^k)^c\)的满足条件的\(k\)跟\(t\)就构造出一组\((x,y,z)\)了。
然后要注意\(exgcd\)求得的一对\(x,y\)要把调整成正数。

11、(Atcoder) ModularPowerEquation

让你构造方程\(n^x\equiv x\pmod m\)的一个正整数解。
\(n,m\le 10^9\)
你的答案不超过\(2*10^{18}\)

Sol:
使用欧拉定理，
令\[x\equiv y\pmod {φ(m)},(x,y>0)\]
以及\[x\equiv n^x\equiv n^y\pmod m\]
继续可推出\[y\equiv n^y\pmod{gcd(m,φ(m))}\]
注意到这与原问题形式一致，故递归求解得到一个\(y\)
此时使用\(EXCRT\)算法，求出\(x\)的值，注意时刻保持\(x,y>0\)，当求出\(x=0\)时把\(x+=M\)就好
关于EXCRT算法相关的一些问题可以参考这里 https://www.cnblogs.com/bestwyj/p/10409806.html
但是以上过程感觉还是有一些疑点，这里说一下个人理解：
（1）首先我一来就是上的扩展欧拉定理，但是那个\(+φ(p)\)不太能处理。
后来发现由于某些奇怪的原因直接写成欧拉定理就挺对的。
（2）题目中要求无解打"-1"，但根据实测情况并不会出现无解，尽管全程\(Assert(c\%d==0)\)，但EXCRT一直工作成功。随了\(10^4\)左右组数据也没出现什么问题。

转载于:https://www.cnblogs.com/bestwyj/p/10290207.html