（最长回文串模板）最长回文 -- hdu -- 3068

最新推荐文章于 2021-07-27 20:59:14 发布

weixin_30697239

最新推荐文章于 2021-07-27 20:59:14 发布

阅读量68

点赞数

文章标签： java php

原文链接：http://www.cnblogs.com/YY56/p/4851382.html

版权

http://acm.hdu.edu.cn/showproblem.php?pid=3068

最长回文

Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 12079 Accepted Submission(s): 4430

Problem Description

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度.
回文就是正反读都是一样的字符串,如aba, abba等

Input

输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S
两组case之间由空行隔开(该空行不用处理)
字符串长度len <= 110000

Output

每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.

Sample Input

aaaa

abab

Sample Output

题意很清楚：就是求一个串s的子串中最长回文串的长度；这类题用到了manacher算法

manacher算法（复制大神的解释）:

定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长

将字符串s从前扫到后for(int i=0;i<strlen(s);++i)来计算p[i],则最大的p[i]就是最长回文串长度,则问题是如何去求p[i]?

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的

分两种情况:

1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串

然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]

2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k

这样的话p[i+k]就不是从1开始

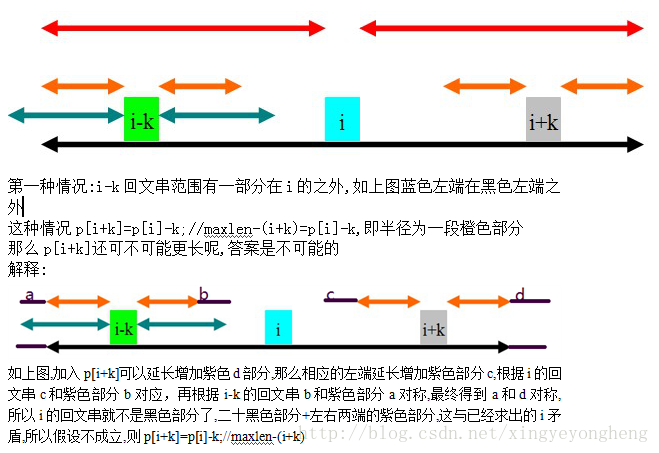
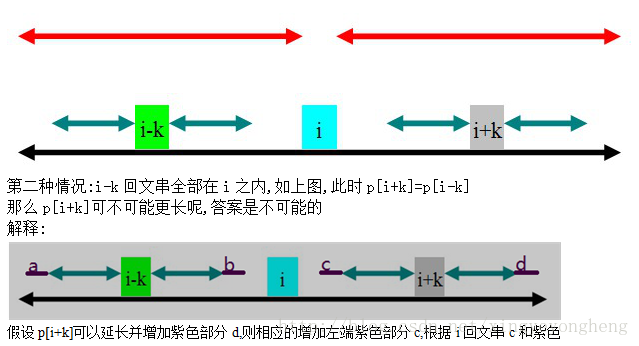
由于回文串的性质,可知i+k这个位置关于i与i-k对称,

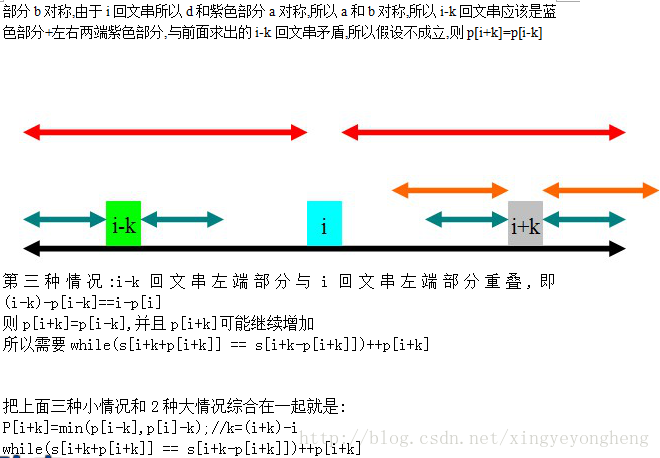
所以p[i+k]分为以下3种情况得出

//黑色是i的回文串范围,蓝色是i-k的回文串范围,

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <limits>
#include <queue>
#include <stack>
#include <vector>
#include <map>

using namespace std;

#define N 244000
#define INF 0x3f3f3f3f
#define PI acos (-1.0)
#define EPS 1e-8
#define met(a, b) memset (a, b, sizeof (a))

char s[N], s1[N];
int p[N];

int manacher()
{
    int index=0, MaxLen = 0, ans=0;

    for(int i=2; s[i]; i++)
    {

        if(MaxLen > i) p[i] = min(MaxLen-i, p[2*index-i]);
        else p[i] = 1;
        while( s[i-p[i]] == s[i+p[i]] )
            p[i]++;

        if(i+p[i]>MaxLen)
        {
            MaxLen = p[i]+i;
            index = i;
        }

        ans = max(ans, p[i]);
    }

    return ans-1;
}

int main()
{
    while(scanf("%s", s1)!=EOF)
    {
        int len = strlen(s1), i;

        memset(s, 0, sizeof(s));

        s[0] = '$';
        for(i=1; i<=len; i++)
        {
            s[i*2-1] = '*';
            s[i*2]   =  s1[i-1];
        }
        s[i*2-1] = '*';
        s[i*2] = '\0';

        printf("%d\n", manacher());
    }
    return 0;
}

View Code

代码2

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;

const int MAXN = 2e6+7;
const int oo = 1e9+37;

char s[MAXN];
int  p[MAXN];

int Manacher(int len)
{
    int id=0, Max=0;

    for(int i=2; i<len; i++)
    {
        p[i] = 1;

        if(p[id]+id > i)
            p[i] = min(p[id*2-i], p[id]+id-i);
        while(s[i+p[i]] == s[i-p[i]])
            p[i]++;
        if(p[id]+id < p[i]+i)
            id = i;

        Max = max(Max, p[i]-1);
    }

    return Max;
}

int main()
{
    int t = 1;

    while(scanf("%s", s), strcmp(s, "END"))
    {
        int N = strlen(s);

        for(int i=N; i>=0; i--)
        {
            s[i+i+2] = s[i];
            s[i+i+1] = '#';
        }
        s[0] = '$';

        printf("Case %d: %d\n", t++, Manacher(N+N+1));
    }

    return 0;
}