POJ 3764 The xor-longest Path 【01字典树&&求路径最大异或和&&YY】

题目传送门：http://poj.org/problem?id=3764

The xor-longest Path

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 9482		Accepted: 1932

Description

In an edge-weighted tree, the xor-length of a path p is defined as the xor sum of the weights of edges on p:

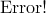
⊕ is the xor operator.

We say a path the xor-longest path if it has the largest xor-length. Given an edge-weighted tree with n nodes, can you find the xor-longest path? 　

Input

The input contains several test cases. The first line of each test case contains an integer n(1<=n<=100000), The following n-1 lines each contains three integers u(0 <= u < n),v(0 <= v < n),w(0 <= w < 2^31), which means there is an edge between node u and v of length w.

Output

For each test case output the xor-length of the xor-longest path.

Sample Input

4
0 1 3
1 2 4
1 3 6

Sample Output

7

Hint

The xor-longest path is 0->1->2, which has length 7 (=3 ⊕ 4)

 

题目大意：

有一棵N个节点的树， 求树上的最大路径异或和。

解题思路：

静态链接表存树。

我们要求一条最大异或和的路径，暴力太恐怖了。

这里巧妙地运用了公式 a ⊕ b ⊕  a = b，也就是说相同的路径被异或两次相当于没有被异或，那么我们从根节点开始 dfs 并且每到一个点就把该点到根节点的路径异或和丢进 01字典树里，然后每次都把当前边和 01字典树里匹配得到最大的异或值（因为在同一棵树，两节点间必定有一个公共祖先，所以起点终点必定是相连的），最后遍历完一棵树得到的最大异或值就是结果。

 

AC code：

 1 ///数组实现
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <cmath>
 7 #define INF 0x3f3f3f3f
 8 #define LL long long int
 9 #define Bit 30
10 using namespace std;
11 const int MAXN = 1e5+10;
12 
13 struct node{
14     int to, va, next;
15 }t[MAXN<<1];
16 
17 int head[MAXN];
18 int ch[MAXN*Bit][2];
19 int value[Bit*MAXN];
20 //bool vis[MAXN];
21 int node_cnt, edge_cnt;
22 int N, ans;
23 
24 inline void init()
25 {
26     ans = 0;
27     node_cnt = 1;
28     edge_cnt = 0;
29     memset(head, -1, sizeof(head));
30     memset(ch[0], 0, sizeof(ch[0]));
31    // memset(vis, false, sizeof(vis));
32 }
33 void add_edge(int u, int v, int w)
34 {
35     t[edge_cnt].next = head[u];
36     t[edge_cnt].to = v;
37     t[edge_cnt].va = w;
38     head[u] = edge_cnt++;
39 }
40 void Insert(int x)
41 {
42     int cur = 0;
43     for(int i = Bit; i >= 0; i--){
44         int index = (x>>i)&1;
45         if(!ch[cur][index]){
46             memset(ch[node_cnt], 0, sizeof(ch[node_cnt]));
47             ch[cur][index] = node_cnt;
48             value[node_cnt++] = 0;
49         }
50     cur = ch[cur][index];
51     }
52     value[cur] = x;
53 }
54 int query(int x)
55 {
56     int cur = 0;
57     for(int i = Bit; i >= 0; i--)
58     {
59         int index = (x>>i)&1;
60         if(ch[cur][index^1]) cur = ch[cur][index^1];
61         else cur = ch[cur][index];
62     }
63     return value[cur]^x;
64 }
65 void solve(int x,int fa, int res)
66 {
67     Insert(res);
68     //vis[x] = true;
69     for(int i = head[x]; i != -1; i = t[i].next){
70         int v = t[i].to;
71         if(v == fa) continue;
72         //if(!vis[v]){
73         ans = max(ans, query(res^t[i].va));
74         solve(v, x, res^t[i].va);
75         //}
76     }
77 }
78 int main()
79 {
80     int a, b, c;
81     while(~scanf("%d", &N)){
82         init();
83         for(int i = 1; i < N; i++){
84             scanf("%d%d%d", &a, &b, &c);
85             a++, b++;
86             add_edge(a, b, c);
87             add_edge(b ,a, c);
88         }
89         solve(1, -1, 0);
90         printf("%d\n", ans);
91     }
92     return 0;
93 }

View Code

 

转载于:https://www.cnblogs.com/ymzjj/p/9544407.html