poj1375Intervals(点到圆的切线）

链接

貌似这样的叫解析几何

重点如何求得过光源到圆的切线与地板的交点x坐标，可以通过角度及距离来算，如图，

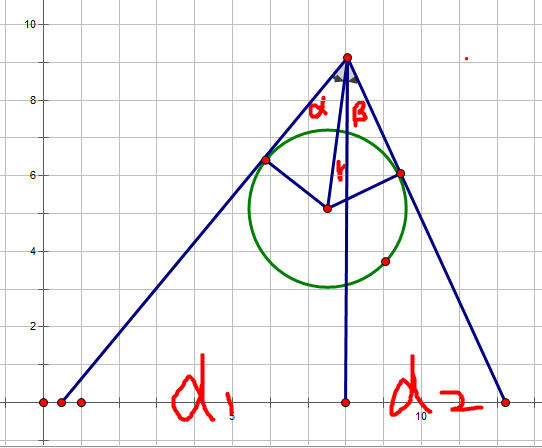
根据距离和半径可以求得角度a、b、r,自然也可以求得d1,d2.

至于方向问题，在求r得时候 可以使r = asin(（p.x-c.x）/d） p为源点，c为圆心 ，d为两点距离。

若在反方向，自然r为负角 ，并不影响最后的结果。

排序后，统计区间就可以了。

 1 #include <iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<stdlib.h>
 6 #include<vector>
 7 #include<cmath>
 8 #include<queue>
 9 #include<set>
10 using namespace std;
11 #define N 505
12 #define LL long long
13 #define INF 0xfffffff
14 const double eps = 1e-8;
15 const double pi = acos(-1.0);
16 const double inf = ~0u>>2;
17 struct point
18 {
19     double x,y;
20     double r;
21     point(double x=0,double y=0):x(x),y(y){}
22 }p[N];
23 struct node
24 {
25     double l,r;
26 }li[N],ans[N];
27 typedef point pointt;
28 pointt operator -(point a,point b)
29 {
30     return point(a.x-b.x,a.y-b.y);
31 }
32 double dis(point a)
33 {
34     return sqrt(a.x*a.x+a.y*a.y);
35 }
36 node cal(point a,point b)
37 {
38     double ang1,ang2,ang3,ang4;
39     double d = dis(a-b);
40     ang1 = asin(a.r/d);
41     ang2 = asin((b.x-a.x)/d);
42     ang3 = ang1+ang2;
43     ang4 = ang2-ang1;
44     //cout<<ang1<<" "<<ang2<<" "<<ang3<<" "<<ang4<<endl;
45     node ll;
46     double l = b.x-b.y*tan(ang3);
47     double r = b.x-b.y*tan(ang4);
48     ll.l = min(l,r);
49     ll.r = max(l,r);
50     return ll;
51 }
52 bool cmp(node a,node b)
53 {
54     return a.l<b.l;
55 }
56 int main()
57 {
58     int n,i;
59     point pp;
60     while(scanf("%d",&n)&&n)
61     {
62         scanf("%lf%lf",&pp.x,&pp.y);
63         for(i = 1; i <= n; i++)
64         scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].r);
65         for(i = 1; i <= n; i++)
66         {
67             li[i] = cal(p[i],pp);
68         }
69         sort(li+1,li+n+1,cmp);
70         int g = 1;
71         ans[g].l = li[1].l;
72         double te = li[1].r;
73         for(i = 2 ; i <= n; i++)
74         {
75             if(li[i].l>te)
76             {
77                 ans[g].r = te;
78                 ans[++g].l = li[i].l;
79             }
80             te = max(te,li[i].r);
81         }
82         ans[g].r = te;
83         for(i = 1; i <= g; i++)
84         printf("%.2f %.2f\n",ans[i].l,ans[i].r);
85         puts("");
86     }
87     return 0;
88 }

View Code

 

转载于:https://www.cnblogs.com/shangyu/p/3891089.html