c语言写一元一次函数图像,一次函数与一元一次不等式（洋葱数学）

一次函数与一元一次不等式(洋葱数学)

一、基本知识点考点：

1、一次函数 y = kx+b (k ≠0 ) 与一元一次不等式的关系：

y＞0,则 kx + b > 0 ； y﹤0,则 kx + b < 0 。

2、如图，直线y=kx+b交坐标轴于A(﹣2，0)，B(0，3)两点，则不等式kx+b＞0的解集是( D )。

A、x＞3 B、﹣2＜x＜3 C、x＜﹣2 D、x＞﹣2

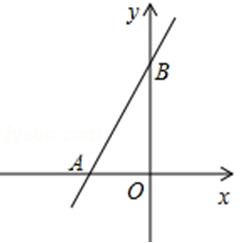
第2题图(1)

3、一次函数y=3x+b和y=ax﹣3的图象如图所示，其交点为P(﹣2，﹣5)，则不等式3x+b＞ax﹣3的解集在数轴上表示正确的是( C)

第3题图(2)

4、已知一次函数y =﹣2x+a与 y = x+b的图象如图所示，则关于x的不等式﹣2x+a≤x+b 的解集是 x ≥ -1 。

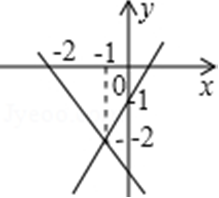
第4题图(3)

5、如图，一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P，则关于x的不等式k1x+b1＞k2x+b2的解集是 x < -2 。 ．

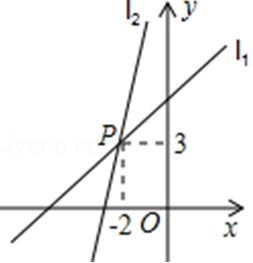
第5题图(4)

二、题型解析：

1、利用一次函数的图象解一元一次不等式kx+b＞0(或 kx+b＜0)

例1、如图，直线y=kx+b经过A(2，1)，B(﹣1，﹣2)两点，则不等式﹣2＜kx+b＜1的解集为( D )

A、﹣2＜x＜2 B、﹣1＜x＜1

C、﹣2＜x＜1 D、﹣1＜x＜2

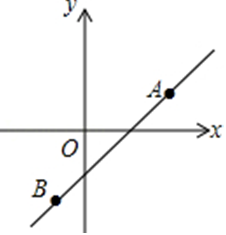
例题1图(5)

解析：由题意可得一次函数图象在y=1的下方时 x＜2，

在y=﹣1的上方时 x＞﹣1，故关于x的不等式﹣2＜kx+b＜1的解集是﹣1＜x＜2．故选D。

例题2、如图，直线y=kx+b交坐标轴于A，B两点，则不等式kx+b≤0的解集在数轴上表示正确的是( B )。

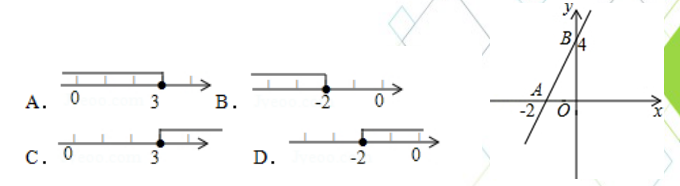
例题2图(6)

解析：由图象可以看出，x轴及其下方的函数图象所对应自变量的取值为x≤﹣2，

所以不等式kx+b≤0的解集是x≤﹣2．故选B。

2、利用一次函数的图象解一元一次不等式 k1x+b1＞k2x+b2(或k1x+b1＜k2x+b2)

例题3、同一直角坐标系中，一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示，则满足y1≥y2的x取值范围是( A)

A．x≤﹣2 B．x≥﹣2 C．x＜﹣2 D．x＞﹣2

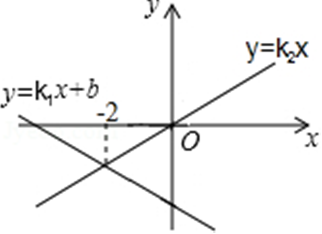
例题3图(7)

解析：当x≤﹣2时，直线l1：y1=k1x+b1 都在直线l2：y2=k2x的上方，

即y1≥y2．故选A。

例题4、如图，直线y=﹣2x 与直线y=kx+b 相交于点A(a，2)，并且直线y=kx+b经过x轴上点B(2，0)

(1)求直线y=kx+b的解析式；

(2)求两条直线与y轴围成的三角形面积；

(3)直接写出不等式(k+2)x+b≥0的解集。

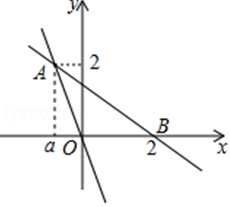
例题4图(8)

解：(1)把A(a，2)代入y=﹣2x中，得﹣2a=2，∴a=﹣1，∴A(﹣1，2)

把A(﹣1，2)，B(2，0)代入y=kx+b中解得：

∴k=﹣2/3 ，b= 4/3，

∴一次函数的解析式是y=﹣ 2/3 x+ 4/3 。

2)设直线AB与y轴交于点C，则C(0，4/3 )

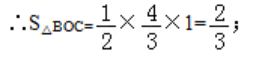
图(9)

(3)不等式(k+2)x+b≥0可以变形为kx+b≥﹣2x，结合图象得到解集为：x≥﹣1。

三、拓展提高：

例题1、

例题1图(10)

例题2、

例题2图(11)

例题3、

例题3图(12)

例题4、

例题4图(13)