O(1)时间复杂度实现入栈、出栈、获得栈中最小元素、获得栈中最大元素(转)

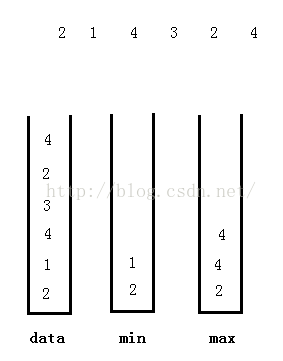
题目要求：定义栈的数据结构，添加min()、max()函数（动态获取当前状态栈中的最小元素、最大元素），要求push()、pop()、min()、max()的时间复杂度都是O(1)。

思路解析：根据栈的后进先出特性，增加辅助栈，来存储当前状态下数据栈中的最小、最大元素。

原文：http://blog.csdn.net/happy309best/article/details/47725935

class Solution:
    def __init__(self):
        self.data=[]
        self.min_data=[]
    def push(self, node):
        self.data.append(node)
        if len(self.min_data)==0 or node<=self.min_data[len(self.min_data)-1]:
            self.min_data.append(node)
    def pop(self):
        if len(self.data)>0:
            val=self.data.pop()
            if val==self.min_data[len(self.min_data)-1]:
                self.min_data.pop()
            return val
    def top(self):
        if len(self.data)>0:
            return self.data[len(self.data)-1]
        return None
    def min(self):
        if len(self.min_data)>0:
            return self.min_data[len(self.min_data)-1]
        return None

 

转载于:https://www.cnblogs.com/gczr/p/7124502.html