题目一:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列数列的定义如下:
f[n]=f[n-1]+f[n-2],且f[1]=1,f[2]=1。
除了面试官直接要求编程实现斐波那契数列之外,还有不少面试题可以看成是斐波那契数列的应用,比如:
题目二:一只青蛙可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级台阶总共有多少种跳法。
首先我们考虑最简单的情况。如果只有一级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳法了:一种是分两次跳,没跳1级;另外一种就是一次跳2级。
接着我们再来讨论一般情况。我们把n级台阶时的跳法看成时n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:
(1)第一次只挑1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);
(2)选择第一次跳两级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。
因此n级台阶的不同跳法的总数f(n) = f(n-1) + f(n-2)。分析到这里我们不难看出这实际上就是斐波那契数列了。
类似的题目还有骨牌覆盖问题,算法-骨牌覆盖问题(矩阵快速幂求Fibonacii)
效率很低的递归算法
我们的教科书上反复用这个问题来讲解递归函数,并不能说明递归的解法最适合这道题目。
long long Fibonacci(unsigned int n)
{
if(n <= 0){
return 0;
}
if(n == 1){
return 1;
}
return Fibonacci(n-1) + Fibonacci(n-2);
}优点:形式简洁,便于人理解
缺点:虽说递归法以空间换时间,但一旦n变大,它的速度的确比非递归法慢得多,例如对n=40,测试递归法所用时间为8~9s;而非递归法只需要远不到1s。
原因是,递归过程中,系统建立堆栈来保存上一层状态信息, 和退栈获取还原系统状态都要有开销的.系统做的事情不少, 所以效率要低.
例如,f(5)的话,实际上会调用这个函数15次,有15个临时栈区,试想f(100)有多吓人。。。一般来说到f(40)以后,普通计算机基本上就不可能计算出来了。
通项公式算法
//使用通项公式Fib(n) = [(1+√5)/2]^n /√5 - [(1-√5)/2]^n /√5
#define ROOT_OF_FIVE sqrt(5.0)
long double Fibonacci(unsigned int n)
{
return (pow(((1 + ROOT_OF_FIVE) / 2.0),n) / ROOT_OF_FIVE -
pow(((1 - ROOT_OF_FIVE) / 2.0),n) / ROOT_OF_FIVE);
}迭代算法
上述递归代码之所以慢是因为重复计算太多,我们只要想办法避免重复计算就行了。比如我们可以把已经得到的数列中间项保存起来,如果下次需要计算的时候我们先查找一下,如果前面已经计算过就不用再重复计算了。
更简单的方法是从下网上算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)…….以此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是O(n)。
#include <iostream>
using namespace std;
long long Fibonacci(unsigned n)
{
int result[2] = {0,1};
if(n < 2)
return result[n];
long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for(unsigned int i = 2; i <= n; i++){
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
int main()
{
int n;
while(cin>>n){
cout<<Fibonacci(n)<<endl;
}
system("pause");
return 0;
}矩阵快速幂算法
时间复杂度O(logn)但不够实用的解法
程序1:
//2*2矩阵结构体
struct Matrix2by2
{
//构造函数
Matrix2by2(long long m_00, long long m_01, long long m_10, long long m_11) :
m00(m_00), m01(m_01), m10(m_10), m11(m_11){}
//数据成员
long long m00;
long long m01;
long long m10;
long long m11;
};
//两个2*2矩阵乘法
Matrix2by2 Matrix_Multiply(const Matrix2by2 matrix1, const Matrix2by2 matrix2)
{
//初始化矩阵
Matrix2by2 matrix12(1, 1, 1, 0);
matrix12.m00 = matrix1.m00*matrix2.m00 + matrix1.m01*matrix2.m10;
matrix12.m01 = matrix1.m00*matrix2.m01 + matrix1.m01*matrix2.m11;
matrix12.m10 = matrix1.m10*matrix2.m00 + matrix1.m11*matrix2.m10;
matrix12.m11 = matrix1.m10*matrix2.m01 + matrix1.m11*matrix2.m11;
return matrix12;
}
//矩阵的快速幂算法
Matrix2by2 Matrix_Fast_Power(unsigned int n)
{
//基矩阵
Matrix2by2 matrix(1, 1, 1, 0);
if (n == 1)
matrix = Matrix2by2(1, 1, 1, 0);
else if (n % 2 == 0)
{
matrix = Matrix_Fast_Power(n / 2);
matrix = Matrix_Multiply(matrix, matrix);
}
else if (n % 2 == 1)
{
matrix = Matrix_Fast_Power((n - 1) / 2);
matrix = Matrix_Multiply(matrix, matrix);
matrix = Matrix_Multiply(matrix, Matrix2by2(1, 1, 1, 0));
}
return matrix;
}
//斐波那契数列计算式
long long P_Fibonacci(unsigned int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
Matrix2by2 Fib_Matrix = Matrix_Fast_Power(n - 1);
return Fib_Matrix.m00;
}
程序2:
#include <iostream>
using namespace std;
const int MOD = 19999997;
struct matrix{ //重载结构体
public:
long long a;
long long b;
long long c;
long long d;
matrix &operator * (matrix &data){ //重载*
long long tempa = a;
long long tempb = b;
long long tempc = c;
long long tempd = d;
a = tempa*data.a%MOD+tempb*data.c%MOD;
b = tempa*data.b%MOD+tempb*data.d%MOD;
c = tempc*data.a%MOD+tempd*data.c%MOD;
d = tempc*data.b%MOD+tempd*data.d%MOD;
return *this;
}
matrix &operator = (matrix &data){ //重载&
a = data.a;
b = data.b;
c = data.c;
d = data.d;
return *this;
}
};
long long fastFibonacci(long n)
{
matrix res = {1,1,1,0};
matrix base = {1,1,1,0};
matrix temp;
n++;
while(n){
if(n&1){
res = res*base;
}
temp = base;
base = base*temp;
n >>=1;
}
return res.d;
}
int main()
{
long n;
while(cin>>n){
cout<<fastFibonacci(n)%MOD<<endl;
}
system("pause");
return 0;
}解法比较
用不同的方法求解斐波那契数列的时间效率大不相同。
使用哪种方法根据实际情况确定,从时间复杂度上来说O(通向公式法)《O(快速幂法)《O(迭代法)《O(递归法)。
第一种基于递归的解法虽然直观但是时间效率很低,在实际软件开发中不会用这种方法,也不可能得到面试官的青睐。
第二种防方法结果不会很准确,但至少能说明问题。
第三种方法把递归的算法用循环实现,极大地提高了时间效率。
第四种方法把斐波那契数列转换成求矩阵的乘方,是一种很有创意的算法。虽然我们可以用O(logn)求得矩阵的n次方,但由于隐含的时间常数较大,很少会有软件采用这种算法。另外实现这种解法的代码也很复杂,不太适用面试。因此第三种方法不是一种实用的算法,不过应聘者可以用它来展现自己的知识面。
完整的程序代码:
#include <iostream>
#define ROOT_OF_FIVE sqrt(5.0)
using namespace std;
//递归方式
long long R_Fibonacci(unsigned int n)
{
if (n <= 0)
return 0;
if (n == 1)
return 1;
return R_Fibonacci(n - 1) + R_Fibonacci(n - 2);
}
//通项公式算法
long double T_Fibonacci(unsigned int n)
{
return (pow(((1 + ROOT_OF_FIVE) / 2.0), n) / ROOT_OF_FIVE -
pow(((1 - ROOT_OF_FIVE) / 2.0), n) / ROOT_OF_FIVE);
}
//迭代方式
long long I_Fibonacci(unsigned int n)
{
int result[2] = { 0, 1 };
if (n < 2)
return result[n];
long long Fib_One = 0;
long long Fib_Two = 1;
long long FibN = 0;
for (unsigned int i = 2; i <= n; ++i)
{
FibN = Fib_One + Fib_Two;
Fib_One = Fib_Two;
Fib_Two = FibN;
}
return FibN;
}
//矩阵快速幂算法
//2*2矩阵结构体
struct Matrix2by2
{
//构造函数
Matrix2by2(long long m_00, long long m_01, long long m_10, long long m_11) :
m00(m_00), m01(m_01), m10(m_10), m11(m_11){}
//数据成员
long long m00;
long long m01;
long long m10;
long long m11;
};
//两个2*2矩阵乘法
Matrix2by2 Matrix_Multiply(const Matrix2by2 matrix1, const Matrix2by2 matrix2)
{
//初始化矩阵
Matrix2by2 matrix12(1, 1, 1, 0);
matrix12.m00 = matrix1.m00*matrix2.m00 + matrix1.m01*matrix2.m10;
matrix12.m01 = matrix1.m00*matrix2.m01 + matrix1.m01*matrix2.m11;
matrix12.m10 = matrix1.m10*matrix2.m00 + matrix1.m11*matrix2.m10;
matrix12.m11 = matrix1.m10*matrix2.m01 + matrix1.m11*matrix2.m11;
return matrix12;
}
//矩阵的快速幂算法
Matrix2by2 Matrix_Fast_Power(unsigned int n)
{
//基矩阵
Matrix2by2 matrix(1, 1, 1, 0);
if (n == 1)
matrix = Matrix2by2(1, 1, 1, 0);
else if (n % 2 == 0)
{
matrix = Matrix_Fast_Power(n / 2);
matrix = Matrix_Multiply(matrix, matrix);
}
else if (n % 2 == 1)
{
matrix = Matrix_Fast_Power((n - 1) / 2);
matrix = Matrix_Multiply(matrix, matrix);
matrix = Matrix_Multiply(matrix, Matrix2by2(1, 1, 1, 0));
}
return matrix;
}
//斐波那契数列计算式
long long P_Fibonacci(unsigned int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
Matrix2by2 Fib_Matrix = Matrix_Fast_Power(n - 1);
return Fib_Matrix.m00;
}
int main()
{
int n;
while (cin >> n)
{
cout << I_Fibonacci(n) << endl;
cout << T_Fibonacci(n) << endl;
cout << P_Fibonacci(n) << endl;
cout << R_Fibonacci(n) << endl;
}
system("pause");
return 0;
}版权声明:本文为博主原创文章,未经博主允许不得转载。







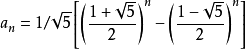














 2158
2158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








