[OI学习笔记]DAG最短路的四种算法整理-floyd,Dijkstra,Bellman-Ford,SPFA

最新推荐文章于 2022-02-13 13:20:14 发布

weixin_30877493

最新推荐文章于 2022-02-13 13:20:14 发布

阅读量606

点赞数

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/sjrb/p/9607238.html

版权

背景

　　开学了，好开心啊！

周末好不容易写篇博客，搞长一点把。。。

最短路概念

这周花了点时间研究最短路问题，那么什么是最短路呢？

摘自百度百科：

最短路问题（short-path problem）是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。基本内容是：若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点（通常是源节点和阱节点）之间总权和最小的路径就是最短路问题。 [1]

我了解的最短路算法有四种——floyd,Dijkstra,Bellman-Ford,SPFA，四种算法各有各的特点，适用的图也有不同。

松弛操作

在学习最短路算法前，首先要了解松弛操作，这是所有最短路算法的核心，即是对于一条边(u,v,w)，比较以中间点k或不以k当中间点时的最短路那个最小，选择小的那条来更新最短路：

if(dist[u]+w<dist[v])dist[v]=dist[u]+w;

(A)Floyd算法时间复杂度O(n³)

1）基于动态规划，本质上是一个三维的DP

2）与其他算法不同，floyd是一个多源最短路径算法，即经过一次floyd后能求出任意两点间的最短路

3）基本思想：dist[i][j][k]是i到j的只以1-k为中间路点的最短路，则dist[i][j][k]=min(dist[i][j][k-1],dist[i][k][k-1]+dist[k][j][k-1]);即选择不以k或以k当中间点时的最小的dist为dist[i][j][k]

4）具体实现：

▶初始化：dist[s][v]=l(s,v)【如果存在边(s,v)】

▶进行松弛操作

3）核心代码

for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(dist[i][k]+dist[k][j]<dist[i][j])
                dist[i][j]=dist[i][k]+dist[k][j]；

(B)Dijkstra算法时间复杂度：堆优化：O((n+m)*log m) 无优化：O(nm)

1）只适用于无负边权的图（有负边要么TLE要么WA）

2）基本思想：不断用已更新的边去更新他所连接的边。

3）具体实现：

▶初始化：dist[s]=0;其余dist[i]=INF;然后把s点加入待处理队列

▶更新：每次以队首节点为基础更新

4）

Q ：如果要求具体的最短路径怎么办？

A ：在更新时如果可以更新就用一个path数组存储这个点是从那个点更新来的，输出时带着输出就可以了

5）

Q：怎么写堆优化？

A：用一个优先队列（原理是小根堆）存储每次更新了的点，依次用这些点去更新这个点所连的边，更新完后就让他出队

6）代码：

#include <bits/stdc++.h>
#define re register
using namespace std;

inline int read() {
    int X=0,w=1; char c=getchar();
    while (c<'0'||c>'9') { if (c=='-') w=-1; c=getchar(); }
    while (c>='0'&&c<='9') X=(X<<3)+(X<<1)+c-'0',c=getchar();
    return X*w;
}

struct Edge { int v,w,nxt; };
Edge e[500010];
int head[100010],cnt=0;

inline void addEdge(int u,int v,int w) {
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}

int n,m,s;
int dis[100010];

struct node { //堆节点
    int u,d;//存储每次更新到的点和它的dist
    //重载运算
    bool operator <(const node& rhs) const {
        return d>rhs.d;
    }
};

inline void Dijkstra() {
    for (re int i=1;i<=n;i++) dis[i]=2147483647;
    dis[s]=0;
    priority_queue<node> Q; //堆
    Q.push((node){s,0});
    while (!Q.empty()) {
        node fr=Q.top(); Q.pop();
        int u=fr.u,d=fr.d;
        if (d!=dis[u]) continue;
        for (re int i=head[u];i;i=e[i].nxt) {
            int v=e[i].v,w=e[i].w;
            if (dis[u]+w<dis[v]) {
                dis[v]=dis[u]+w;
                Q.push((node){v,dis[v]});
            }
        }
    }
}

int main() {
    n=read(),m=read(),s=read();
    for (re int i=1;i<=m;i++) {
        int X=read(),Y=read(),Z=read();
        addEdge(X,Y,Z);
    }
    Dijkstra();
    for (re int i=1;i<=n;i++) printf("%d ",dis[i]);
    return 0;
}

(C)Bellman-ford算法时间复杂度：O(mn)

1）基于动态规划

2）可以用来判负环

3）如果没有负环，至多更新n-1轮或者某轮没有更新即可出解

4）判负环：如果更新第n-1环之后还有边能更新，就有负环

5）具体实现：

1）dist[s]=0;其余=INF

2）更新n-1轮，其中每轮：

1）对于每一条边，如果if(dist[u]+w<dist[v])dist[v]=dist[u]+w;并且把updated标记改为有更新

2）更完每条边后，如果updateed标记是没更新，就break，因为这时已经更新结束，并且这样肯定没负环

3）最后把updated改为0，进行下一轮

4)再单独更新一轮，如果这单独一轮中有更新，就判为有负环

6）生动形象的演示：

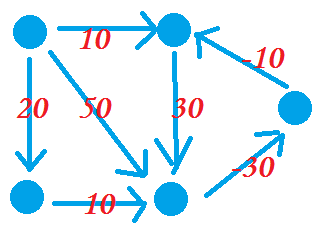
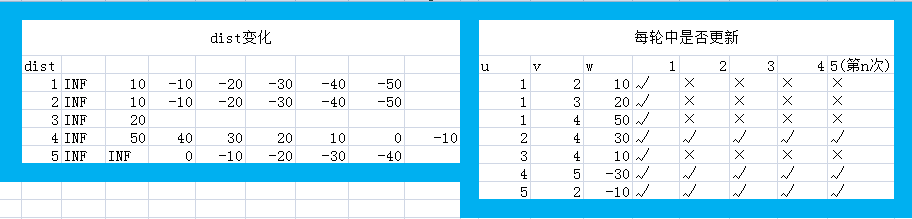
#include<cstdio>
#define INF 2147483647
#define MAX 10010
struct Edge{
    int u,v,w;
}edge[MAX];
int n,m,s,t,dist[MAX];
void BellmanFord(){
    int updated=0;
    for(int j=1;j<=n-1;j++){
        for(int i=1;i<=m;i++)
            if(dist[edge[i].u]+edge[i].w<dist[edge[i].v]){
                dist[edge[i].v]=dist[edge[i].u]+edge[i].w;
                updated=1;
            }
        if(!updated)break;
        updated=0;
    }
    for(int i=1;i<=m;i++)
        if(dist[edge[i].u]+edge[i].w<dist[edge[i].v]){
            printf("Orz");
            return;
        }
    printf("%d",dist[t]);    
}
int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    int X,Y,Z;
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&X,&Y,&Z);
        edge[i].u=X;
        edge[i].v=Y;
        edge[i].w=Z;
    }
    BellmanFord();
    return 0;
}

(D)SPFA 常被卡时间复杂度：最坏：O(nm) 一般：不知道

1）关于SPFA，他死了

2）原因是在NOI中Dijkstra和SPFA这对难兄难弟经常其中一个被卡数据导致不能通过，而SPFA最经常

3）和Dijkstra有点像，我有时候都分不清

3）SPFA也是用一个队列（不是优先队列），第一步从s点开始，s入队，对于队中的每一个元素，广度遍历其所有出边（u，v，w），并对其进行松弛，如果松弛可以进行，就让v入队，搜算完成后，让u出队，进行下一轮搜索，直至队列空

4）是bellmanford的优化

5）具体实现：

1）初始化：dist[s]=0;其余=INF；

2）从s开始搜索，进行松弛，直至队列空

6）代码：

#include <bits/stdc++.h>
#define ll long long
#define MAXM 500005
#define MAXN 10005
using namespace std;
    int n,m,s,sz,st,en;
    int Q[4000005],f[MAXN],to[MAXM<<1],nex[MAXM<<1],v[MAXM<<1],las[MAXN];
    bool inq[MAXN];
int inline read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void ins(int x,int y,int z)
{
    sz++;to[sz]=y;v[sz]=z;nex[sz]=las[x];las[x]=sz;
}
void spfa()
{
    memset(f,127/2,sizeof(f));
    f[s]=0;Q[st=en=1]=s;
    while (st<=en)
    {
        int x=Q[st++];
        inq[x]=false;
        for (int i=las[x];i;i=nex[i])
        if (f[x]+v[i]<f[to[i]])
        {
            f[to[i]]=f[x]+v[i];
            if (!inq[to[i]])
            {
                inq[to[i]]=true;
                Q[++en]=to[i];
            }
        }
    }
}
int main()
{
    n=read(),m=read(),s=read();
    for (int i=1;i<=m;i++)
    {
        int x=read(),y=read(),z=read();
        ins(x,y,z);
    }
    spfa(); 
    for (int i=1;i<=n;i++)
        printf("%d%c",f[i]>1e9?2147483647:f[i],i==n?'\n':' ');
    return 0;
}

以上就是关于DAG最短路的算法，各种算法各有各的优缺点，主要体现在时空复杂度上，要谨慎使用

一道模板题(普及-难度)

关于图论的内容的话再写一个拓补排序就不写了（表示图论从暑假看到现在已经看吐了）

求推荐.

转载于:https://www.cnblogs.com/sjrb/p/9607238.html

weixin_30877493

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
[OI学习笔记]DAG最短路的四种算法整理-floyd,Dijkstra,Bellman-Ford,SPFA

背景　　开学了，好开心啊！周末好不容易写篇博客，搞长一点把。。。最短路概念这周花了点时间研究最短路问题，那么什么是最短路呢？摘自百度百科：最短路问题（short-path problem）是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。基本内容是：若网络中的每条边都有一个数值（长度、成本、时...
复制链接

扫一扫