CodeForces 339D————线段树之单点修改

D. Xenia and Bit Operations

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Xenia the beginner programmer has a sequence a, consisting of 2n non-negative integers: a1, a2, ..., a2n. Xenia is currently studying bit operations. To better understand how they work, Xenia decided to calculate some value v for a.

Namely, it takes several iterations to calculate value v. At the first iteration, Xenia writes a new sequence a1 or a2, a3 or a4, ..., a2n - 1 or a2n, consisting of 2n - 1 elements. In other words, she writes down the bit-wise OR of adjacent elements of sequence a. At the second iteration, Xenia writes the bitwise exclusive OR of adjacent elements of the sequence obtained after the first iteration. At the third iteration Xenia writes the bitwise OR of the adjacent elements of the sequence obtained after the second iteration. And so on; the operations of bitwise exclusive OR and bitwise OR alternate. In the end, she obtains a sequence consisting of one element, and that element is v.

Let's consider an example. Suppose that sequence a = (1, 2, 3, 4). Then let's write down all the transformations (1, 2, 3, 4)  → (1 or 2 = 3, 3 or 4 = 7)  →  (3 xor 7 = 4). The result is v = 4.

You are given Xenia's initial sequence. But to calculate value v for a given sequence would be too easy, so you are given additional mqueries. Each query is a pair of integers p, b. Query p, b means that you need to perform the assignment ap = b. After each query, you need to print the new value v for the new sequence a.

Input

The first line contains two integers n and m (1 ≤ n ≤ 17, 1 ≤ m ≤ 105). The next line contains 2n integers a1, a2, ..., a2n (0 ≤ ai < 230). Each of the next m lines contains queries. The i-th line contains integers pi, bi (1 ≤ pi ≤ 2n, 0 ≤ bi < 230) — the i-th query.

Output

Print m integers — the i-th integer denotes value v for sequence a after the i-th query.

Sample test(s)

input

2 4
1 6 3 5
1 4
3 4
1 2
1 2

output

1
3
3
3

这个问题的描述就强烈的暗示我们用线段树来做了。

不过这个和普通的单点修改略有不同，因为有两种不同的操作，or和xor。

我们所需要判断的就是什么时候用or、xor。

有一点不难发现，or和xor这两个操作一定是交替进行的，这是第一点。

于是我们可以传递一个参数，通过判断这个参数的正负或者奇偶等来决定进行哪一种操作。

这一点很好想到。

但是同样的，我们应该有一个疑问，那就是第一次传入的这个judge参数在满足什么情况下是or（xor）？

也就是说，我们必须确定这段区间是先or还是先xor的。

通过一些分析我们发现：

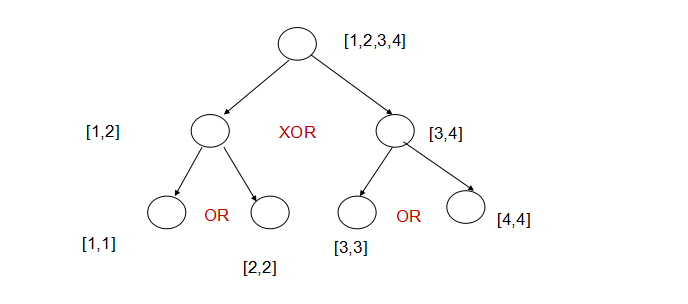
当题目中的n是偶数的时候,例如n = 2(总数为2^2）

[1,2,3,4]

那么操作是如下图所示：

 

当题目中的n是奇数的时候，例如n = 1。（总数为2^1)

[1,2]

那么直接就是1 or 2

以上两种操作顺序是不同的，那么就可以先对n进行一下奇偶性的判断，然后觉得传入的参数是什么。

附AC代码，其中关键地方有注释，应该可以看懂。

<span style="font-family:Microsoft YaHei;font-size:14px;">#include <stdio.h>
#include <string.h>
#define maxn 1<<17

typedef struct{
	int left,right,mid;
	int value;
}Tree;

Tree tree[maxn << 2];
int num[maxn+1];
int N;
void Build(int root,int left,int right,int judge) 
{
	tree[root].left = left;
	tree[root].right = right;
	tree[root].mid = (tree[root].left + tree[root].right) >> 1;
	if(left == right){//最后一个叶节点不做or和xor的处理,递归出口 
		tree[root].value = num[left];
		return ;
	}
	int mid = (left + right) >> 1;
	//-1,1交替进行代表了or和xor的交替进行 
	Build(root << 1,left,mid,-judge);
	Build(root << 1|1,mid+1,right,-judge);
	if(judge == 1)//judge == 1,xor操作 
		tree[root].value = (tree[root<<1].value ^ tree[root<<1|1].value);
	else//否则做or操作 
		tree[root].value = (tree[root<<1].value | tree[root<<1|1].value);
}
void Update(int root,int index,int value,int judge)
{
	if(tree[root].left == tree[root].right && tree[root].right == index){
		tree[root].value = value;
		return ;
	}
	if(index <= tree[root].mid)
		Update(root<<1,index,value,-judge);
	else if(tree[root].mid < index)
		Update(root<<1|1,index,value,-judge);
	if(judge == 1)
		tree[root].value = (tree[root<<1].value ^ tree[root<<1|1].value);
	else
		tree[root].value = (tree[root<<1].value | tree[root<<1|1].value);
}
int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m) != EOF){
		int pos,value,judge;
		memset(tree,0,sizeof(tree));
		memset(num,0,sizeof(num));
		int N = 1 << n;//数据总个数 
		for(int i = 1 ; i <= N ; ++i )
			scanf("%d",&num[i]);
		if(n % 2 == 1)//奇偶不同策略不同 
			judge = -1;
		else
			judge = 1;
		Build(1,1,N,judge);
		while(m--){
			scanf("%d%d",&pos,&value);
			Update(1,pos,value,judge);
			printf("%d\n",tree[1].value);
		} 
	}
}</span>

转载于:https://www.cnblogs.com/sixdaycoder/p/4348358.html