机器学习周志华- 第六章学习笔记6.1-6.4

最新推荐文章于 2024-09-09 14:44:05 发布

weixin_30915275

最新推荐文章于 2024-09-09 14:44:05 发布

阅读量434

点赞数 1

文章标签：人工智能 matlab 数据结构与算法

原文链接：http://www.cnblogs.com/is-Tina/p/7451105.html

版权

本周学习了6.1-6.4节

间隔与支持向量

对于二分类学习，假设现在的数据是线性可分的，这时分类学习最基本的想法就是找到一个合适的超平面，该超平面能够将不同类别的样本分开，类似二维平面使用ax+by+c=0来表示，超平面实际上表示的就是高维的平面。

函数间隔就是|w’x+b|，而几何间隔就是点到超平面的距离

函数间隔不适合用来最大化间隔，因此这里我们要找的最大间隔指的是几何间隔，于是最大间隔分类器的目标函数定义为：max y y=2/||w||

对偶问题

SVM的基本型本身是一个凸二次规划问题，可直接用优化计算包求解，也可转化为更高效的“对偶问题”。

1.引入拉格朗日乘子得到拉格朗日函数

2.L(w,b,a)对w和b的偏导为零可得

3.回代

最终模型

KKT条件

SMO算法

核函数

把训练集的向量点转到高维的非线性映射函数，用核函数取代非线性映射的内积

在SVM转化为最优化问题时求解的公式计算大多都是以内积形式出现

==如果原始空间是有限维（属性数有限），那么一定存在一个高维特征空间使样本可分==

推导

常见的核函数

核函数的组合

这三个表达式得到的结果都为核函数

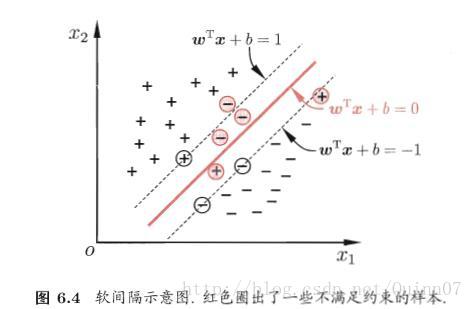
软间隔与正则化

引入软间隔，允许在一些样本上不满足约束

软间隔示意图

硬间隔

软间隔允许有些样本不满足约束

在最大化间隔的同时，不满足约束的样本应尽可能少。

使用αn和βn来构造拉格朗日函数

软间隔的对偶形式

算法步骤

三种常见的替代损失函数

使用matlab自带的svmtrain函数

% 使用SVM(支持向量机)分割两类点并画出图形
XY1 = 2 + rand(100,2); % 随机产生100行2列在2-3之间的点
XY2 = 3+ rand(100,2);% 随机产生100行2列在3-4之间的点
XY = [XY1;XY2]; % 合并两点
Classify =[zeros(100,1);ones(100,1)]; % 第一类点用0表示，第二类点用1表示
Sample = 2+ 2*rand(100,2); % 测试点
%figure(1);
%plot(XY1(:,1),XY1(:,2),'r*'); % 第一类点用红色表示
%hold on;
%plot(XY2(:,1),XY2(:,2),'b*'); % 第二类点用蓝色表示
% 训练SVM
SVM = svmtrain(XY,Classify,'showplot',true);
% 给测试点分类，并作出最大间隔超平面(一条直线)
svmclassify(SVM,Sample,'showplot',true);

libsvm在MATLAB中的使用

下载libsvm
设置路径
mex -setup命令或者直接运行make.m文件编译C++文件

libsvmread(heart_scale)

libsvmread 主要用于读取数据

这里的数据是非matlab下的.mat数据，比如说是.txt，.data等等，这个时候需要使用libsvmread函数进行转化为matlab可识别数据，比如自带的数据是heart_scale数据，那么导入到matlab有两种方式，一种使用libsvmread函数，在matlab下直接libsvmread(heart_scale);第二种方式为点击matlab的‘导入数据’按钮，然后导向heart_scale所在位置，直接选择就可以了

libsvmwrite(‘filename’,label_vector, instance_matrix)

libsvmwrite写函数

libsvmwrite(‘filename’,label_vector, instance_matrix);

label_vector是标签，instance_matrix为数据矩阵（注意这个数据必须是稀疏矩阵，就是里面的数据不包含没用的数据（比如很多0），有这样的数据应该去掉再存）

model=svmtrain(label,data,Libsvm_options);

svmtrain训练函数，训练数据产生模型的
cmd: -t=0时线性核。-t=1多项式核，-t=2，径向基函数（高斯），-t=3，sigmoid核函数
==-g为核函数的参数系数，-c为惩罚因子系数，-v为交叉验证的数，默认为5.==

Libsvm_options

怎么选择呢？libsvm_options:重要的是-t，以及交叉验证时的-v

==-s svm类型：SVM设置类型，一般默认0不用设置==

0 -- C-SVC（多类分类）

1 --v-SVC（多类分类）

2 –一类SVM

3 -- e –SVR

4 -- v-SVR

==-t 核函数类型：核函数设置类型(默认2)==

0 –线性：u'v

1 –多项式：(r*u'v + coef0)^degree

2 – RBF函数：exp(-gamma|u-v|^2)

3 –sigmoid：tanh(r*u'v + coef0)

-d degree：核函数中的degree设置(针对多项式核函数)(默认3)

==-g r(gama)：核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/ k)==

-r coef0：核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)

==-c cost：设置C-SVC，e -SVR和v-SVR的参数(损失函数)(默认1)==

-n nu：设置v-SVC，一类SVM和v- SVR的参数(默认0.5)

-p p：设置e -SVR 中损失函数p的值(默认0.1)

-m cachesize：设置cache内存大小，以MB为单位(默认40)

-e eps：设置允许的终止判据(默认0.001)

-h shrinking：是否使用启发式，0或1(默认1)

-wi weight：设置第几类的参数C为weight*C(C-SVC中的C)(默认1)

==-v n: n-fold交互检验模式，n为fold的个数，必须大于等于2==

返回的model

-Parameters: 参数。

-nr_class: 类的数目。

-totalSV:总的支持向量数目。

-rho: -判决函数wx+b的b。

-Label: 每个类的标签。

-ProbA: 成对的概率信息，如果b是 0则为空。

-ProbB: 成对的概率信息，如果b是 0则为空。

-nSV: 每个类的支持向量

-sv_coef:判决函数的系数

-SVs:支持向量。

如果指定了'-v',那么就实施了交叉验证，而且返回是交叉验证的正确率。

[predicted_label]=svmpredict(testing_label_vector,testing_instance_matrix, model, ‘libsvm_options’)

或者
[predicted_label,accuracy,decision_values/prob_estimates]= svmpredict(testing_label_vector,testing_instance_matrix,model,’libsvm_options’)
输入为
输出为三个参数，预测的类型，准确率，评估值（非分类问题用着）

%加载数据集 
load  heart_scale.mat
%返回heart_scale_inst(instance_matrix数据矩阵） heart_scale_label是标签
%径向基函数（高斯）训练
model = svmtrain(heart_scale_label,heart_scale_inst,'-t 2');
[predict_label,accuracy,decision_values] = svmpredict(heart_scale_label,heart_scale_inst,model);

%% 加载数据
% * 最终data格式：m*n，m样本数，n维度
% * label:m*1  标签为-1与1这两类
clc
clear
close all
data = load('data_test1.mat');
data = data.data';
%选择训练样本个数
num_train = 80;
%构造随机选择序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
gscatter(train_data(:,1),train_data(:,2),train_data(:,3));
label_train = train_data(:,end);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
predict = zeros(length(test_data),1);
%% ----训练模型并预测分类
model = svmtrain(label_train,train_data(:,1:end-1),'-t 2');
% -t = 2 选择径向基函数核 
true_num = 0;
for i = 1:length(test_data)
    % 作为预测，svmpredict第一个参数随便给个就可以
    predict(i) = svmpredict(1,test_data(i,1:end-1),model);
end
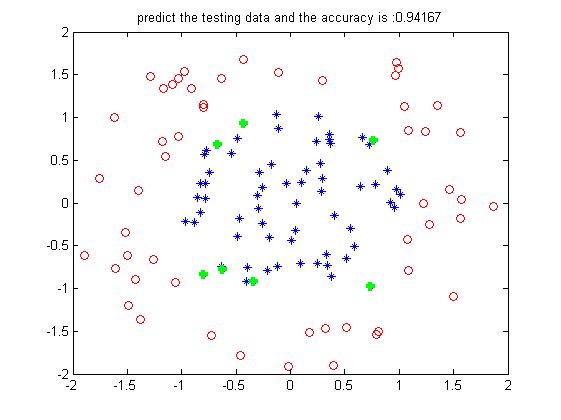
%% 显示结果
figure;
index1 = find(predict==1);
data1 = (test_data(index1,:))';
plot(data1(1,:),data1(2,:),'or');
hold on
index2 = find(predict==-1);
data2 = (test_data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
indexw = find(predict~=(label_test));
dataw = (test_data(indexw,:))';
plot(dataw(1,:),dataw(2,:),'+g','LineWidth',3);
accuracy = length(find(predict==label_test))/length(test_data);
title(['predict the testing data and the accuracy is :',num2str(accuracy)]);

补充

Matlab中存储及读取数据 sava load

我们在使用MATLAB过程中，免不了希望将运算过程中的某些数据「储存」起来，以便下次使用再「读取」利用。「储存」和「读取」的指令分别是save及load

save的数据型态又分为
(1)双位元格式 (binary format) 的 MAT-file

MAT-file 是以双位元字元储存，可让电脑在读出/入(input/output) 速率加快，其格式为test.mat（test为档名），MATLAB将档案的型态预设为MAT-file；

(2) ASCII 格式的 ASCII-file。
ASCII-file则是以可辨识的字元储存，但会降低电脑在读出/入的速率，其格式为test.dat（test为档名）。

==如果你的数据是只在MATLAB中产生及被使用，那最好使用MAT-file。ASCII-file则必须用在当数据档要为其它不是MATLAB的应用软体读取时==

当save成MAT档是储存变数本身，而非直接储存变数的数据；而save成ASCII档则是直接储存变数的数值。

>> A=[1 2 3; 4 5 6];
>> save data.dat A -ascii %是将A阵列的数值存入data这个ASCII-file
>> type data.dat % type 指令可以将 data.dat 的内容列出
>> load data.dat
>> x4=data(:,1); % 令 x4 为 data 的第一列数据
>> y4=data(:,2); % 令 y4 为 data 的第二列数据
>> z4=data(:,3); % 令 z4 为 data 的第三列数据

% 先产生二个列阵列 (row array} x, y
>> x=1:5; y=11:15;
>> save data1 x y 
% 是将 x,y 二个变数的数值存入 data1 这个MAT-file，
%即data1其实是data1.mat。data1.mat 的内容为变数x, y，而非(1:5, 11:15) 的数据
>> load data1 % 读取 data1.mat 档

转载于:https://www.cnblogs.com/is-Tina/p/7451105.html