无限循环小数四则运算_中学最烧脑的问题之颠覆三观——0.999无限循环竟然等于1？...

写在前面

别以为你穿个贵点的马甲我就不认识你是1了！

疑惑不解的0.999...

在中学我相信大家一定听说过

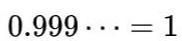
这个传说吧，我记得当时是一个同学给我讲的，奈何我当时年少轻狂，一口否认肯定不等于，还大言不惭地说什么无限靠近永不相交。现在想想是我年少无知。

那么这个和1靠的非常近的无限循环小数到底等不等于1呢？阿拉丁今天就好好和大家探讨一下(为了让更多的人可以听懂，阿拉丁不会讲关于实数理论的严格证明)

一些所谓的证明

在正式讨论之前我们先来看看“民间数学家”的非主流证明

分数证明

这个证明真的是华丽中透着一丝丝朴素，矛盾中透着一丝丝合理，妖艳中透着一丝丝淡雅......

看似无懈可击、天衣无缝，实则偷换概念，利用人的惯性思维。

方程证明

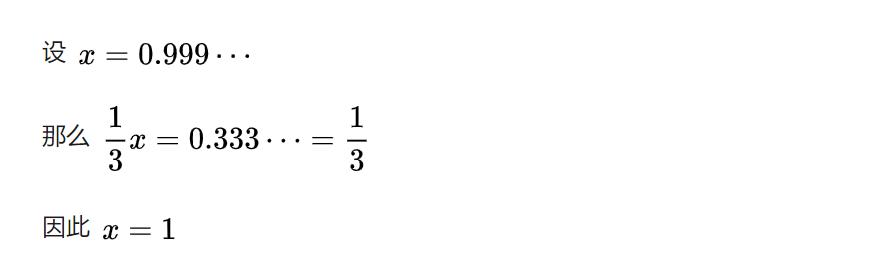
哇塞，好棒棒，又是一个看似天衣无缝，闭月羞花、倾国倾城.....咦好像不太对，哎呀别在意。这样证明的存在到底是人性的扭曲还是道德的沦丧？

阿拉丁有话说

以上两种证明是现在市面上比较普遍的证明。当然，这种证明的存在即有合理性，我们只能说这些证明有问题，但不能说他们不应该存在，阿拉丁觉得有了这些的存在，才能引发人们对于数学的思考。

那为什么说这些证明是不对的呢？其实他们只是偷换了概念，利用惯性思维罢了。在中学课本上从来没有任何地方定义过无限小数的加、减、乘、除四则运算吧，所以无论说

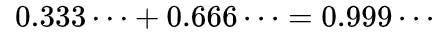
还是

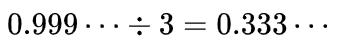
都是我们惯性思维照搬有限小数的四则运算罢了。他们如何相等，我们并不知道。

相等的意义

那么下面阿拉丁就尽量用大家都能听得懂的方式来解释一下为什么

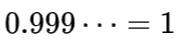
分数相等的意义

我们小学学过自然数，在自然数范围内，表示是唯一的，比如说2=2一定成立，不可能在自然数中除了2还有什么数字 A ，使得 A=2。

但是上了上了初中以后我们学习了有理数，其实就是说分数的概念。那么表示就不唯一了。比如还是2，我们可以表示成

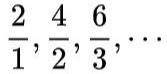
等等

其实分数这样的表示是一种“家族式表示”就是一种类的概念，当数系从自然数扩展到有理数，每一个数都是有无限多个相等的数组成的类，我们称之为 “等价类” ，所谓两个分数相同，指的就是他们两个属于同一个等价类。

可以说在自然数系里每一个数都是孤独的，而在有理数系中每一个数都有着无数的和它相等等 小伙伴陪着它。也就是说分数或者有理数是以等价类的形式存在的

实数相等的意义

那么随着数系的扩充有理数扩展到实数，这里可能有一点点小难理解，需要用到极限的概念。

我们表示一个数的常用方法是把任意一个实数看做收敛的有理数列。这就是说，所谓实数，就是 “极限相同的有理数列” 的共同体，因此它也是一个等价类。

举个例子，比如两个有理数列

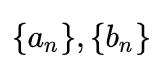
满足

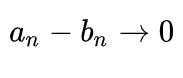
,则说两者属于一个等价类。

我们把每一个等价类都当做一个对象来看待，这里的对象指的是一列有理数，比如

根号2 就可以表示为

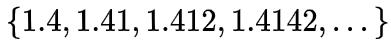
(即根号2 的不足近似值组成)，也可以表示为

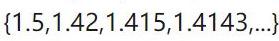
(即根号2的过剩近似)。因此我们可以看到 根号2有着无数的极限相同的有理数列表示，它们属于同一个等价类。

因此我们说

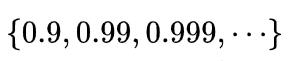
和

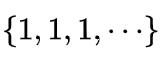
都是收敛到1的有理数列。在这个意义上，它们属于同一个等价类，代表同一个实数。

于是可以写成

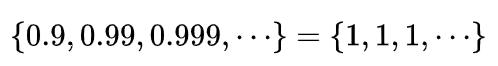
也就是我们今天的主题

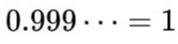
阿拉丁有话说

由此看来，有理数的表示不唯一，由彼此相等的分数构成等价类。而实数表示也不唯一，可以表示为收敛的无限数列，具有相同极限的有理数列构成等价类。

因此

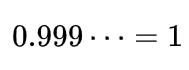
不再是数与数之间的概念，而是类与类之间的概念。

今天你学废了吗？

后记

这个问题其实对于中学生来说有点超纲，但是实实在在可以作为数学类的科普，阿拉丁在网上看到很多关于这方面的讨论，大多数是网络喷子啥也不懂乱喷人。不过有兴趣的同学也可以去了解一下这个问题的严谨证明，通常可以用戴德金分割和柯西序列法来证明。

如果您喜欢作者，您的关注与点赞都是对作者最大的鼓励！