复平面上gamma函数_逐渐硬核的函数展开——洛朗级数、Mittag-Leffler和Weierstrass定理...

从幂级数到洛朗级数

在传统微积分的范畴内，幂级数

是一个非常有效的函数近似工具。它不仅能够帮助我们为函数找出合适的多项式近似，还能够有效地解决极限里一类未定式问题：

然而幂级数也有它的局限性，它只能在全纯函数的解析点处展开，而且很多时候都无法在函数的定义域内完全收敛。比如

在x=0处就无法产生幂级数展开。但事实上，如果我们对指数函数进行换元，可以得到一个别样的展开式。

对于

，令

，可得：

读者不难验证这个展开式在

定义域内都收敛

此类展开式推广开就是洛朗级数（Laurent series）：

。有了它，我们就可以得到亚纯函数在极点附近的近似。在分析时，洛朗级数会被分解为主部和正则部：

仔细观察，我们可以发现主部和正则部本质上是两个幂级数，所以它们会有对应的收敛半径。设主部的收敛半径为r，正则部为R，则洛朗级数的收敛域在复平面上为圆环：

这也意味着函数只要在某一圆环内解析，就可以产生洛朗展开。现在我们设围道

如下：

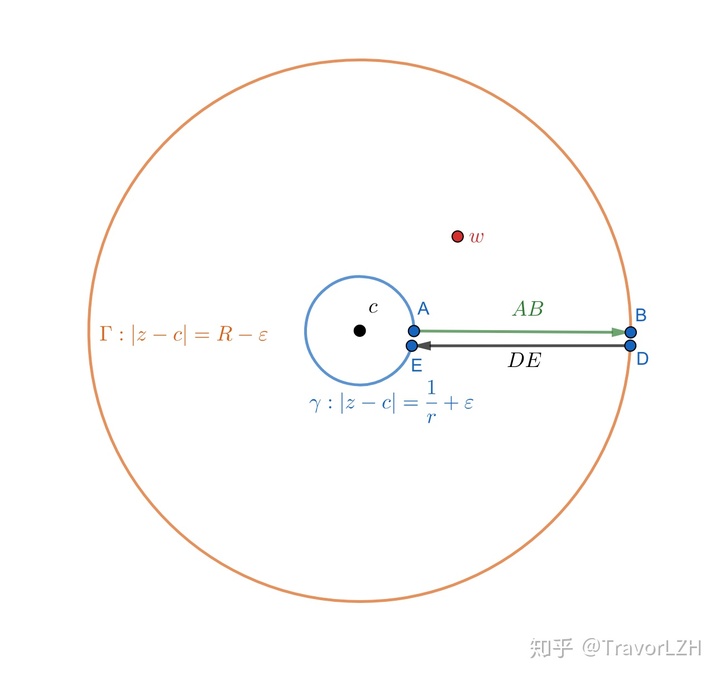
根据条件，我们知道f(z)在围道内部和围道上都解析。所以根据柯西积分公式有：

由于AB与DE方向刚好相反，两者刚好可以抵消，所以上面的式子变成了：

在

上，有

，所以

。于是，橙色部分可以通过几何级数被变换为正则部：

在

上，有

，所以蓝色部分可以变换为主部：

将这两个结果代入(1)式，得：

根据柯西积分公式，易证对于任意自然数k，

且对于任意正整数n，