MCMC贝叶斯方法用于加筋复合板的冲击载荷识别

前言

本文提出了一种统计方法，用于使用贝叶斯推理识别加筋复合板上的冲击位置和冲击力历史，其中明确包括来自建模误差和测量噪声的不确定性。通过使用一组参数表示冲击载荷，首先将空间域（撞击位置）和时域（冲击力历史）中的冲击载荷识别问题转换为参数识别问题。马尔可夫链蒙特卡罗方法用于对后验分布进行采样以估计影响参数。使用噪声有限元数据进行数值模拟研究，以证明所提方法的有效性。

简介

在航空航天工业中，复合材料已广泛用于商用和军用车辆的主要结构加载部件。设计复合结构的主要问题之一是由低速冲击引起的内部损坏，主要是分层，这些损坏难以检测并且可能显着降低结构的完整性。传感技术的最新进展以及计算和通信的发展使人们对调查和开发结构健康监测技术产生了浓厚的兴趣，这些技术可作为内置诊断系统整合到复合结构中。 对于复合结构，要准确评估损伤程度和残余强度，高效可靠的健康监测系统的首要任务是在发生碰撞事件时检测和识别冲击负荷。

贝叶斯方法对冲击载荷的识别

贝叶斯统计识别框架的主要思想是它处理系统参数，通常用向量表示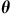，作为联合分布的随机变量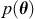。与确定性识别方法相反，该统计方法旨在计算给定测量数据集的不确定系统参数的后验（更新）分布。然后，最终参数估计可以作为后验的平均值或使用最大化后验分布的值。因此，在本研究中，要将贝叶斯框架结合到冲击载荷识别中，第一步是使用一组参数来表示冲击载荷。

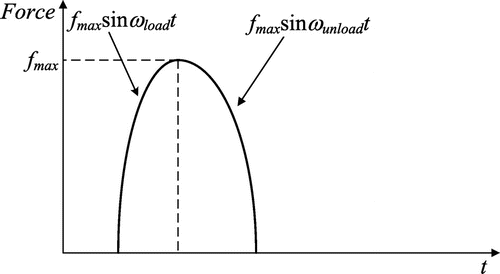
图1.复合结构冲击力历史的近似表示

MCMC方法

作为一种强大的随机模拟技术，蒙特卡罗（MC）方法已被广泛用于研究与概率相关的问题。它可以非常高效，尤其是在可以生成独立样本时。遗憾的是，贝叶斯推断中使用的后验分布通常很复杂，因此很难为标准MC方法绘制独立样本。在这种情况下，MCMC模拟通常被用作采样的替代选择。MCMC的结果是样本的依赖序列（马尔可夫链），其具有等于目标分布的平稳分布。

数值模拟研究

正向碰撞模型的比较

为了证明所提出的冲击载荷识别方法的有效性，本节将进行数值研究。来自广泛使用的有限元软件MSC的噪声响应。Nastran用作测量数据。首先使用有限元法和第4节中给出的方法对前向碰撞模型进行比较。为方便起见，下文中，使用有限元方法的正向冲击模型称为有限元模型，本研究中使用的模型简称为前向冲击模型。

图4.数值研究中的加强复合板和传感器放置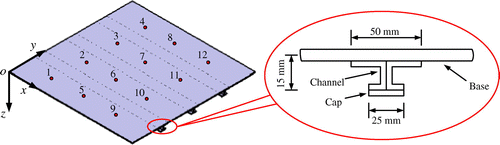

图5.正向冲击模型和有限元模型对冲击响应的比较。

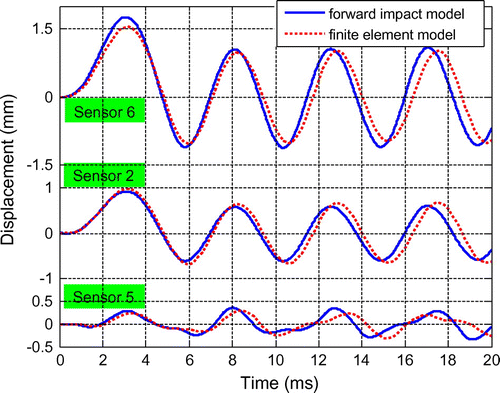
图6.数值研究中使用的冲击力历史

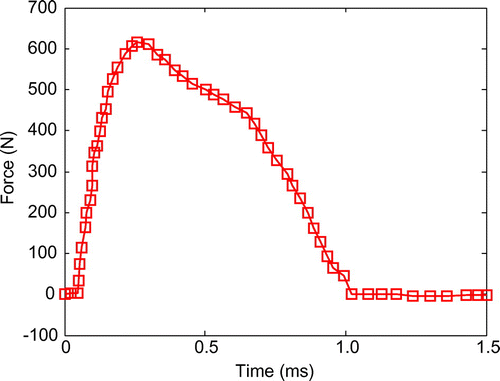
图7. MCMC在对海湾产生影响时的冲击参数样本，测量噪声水平为5％。

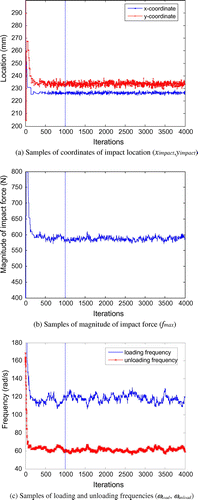
图8.已确定参数的直方图和拟合边际PDF，测量噪声水平为5％。

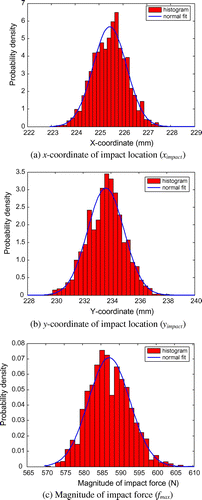
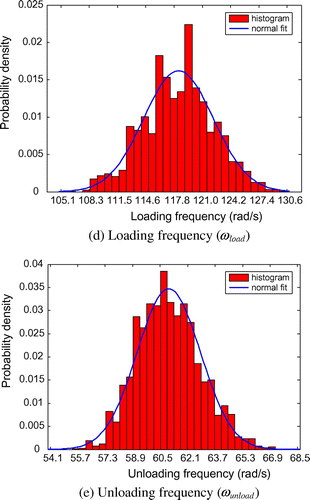
图9.已识别参数的正常图，测量噪声水平为5％。

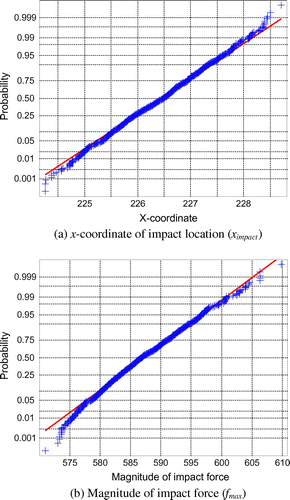
图10.海湾的识别冲击力历史，置信区间为90％，测量噪声水平为5％。

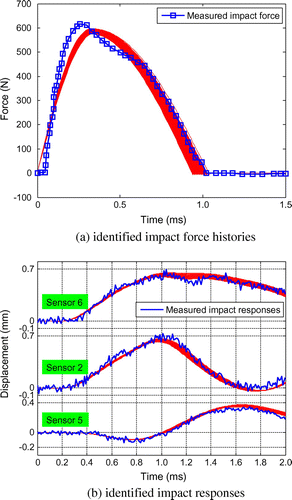
图11.确定法兰上的冲击力历史，置信区间为90％，测量噪声水平为5％。

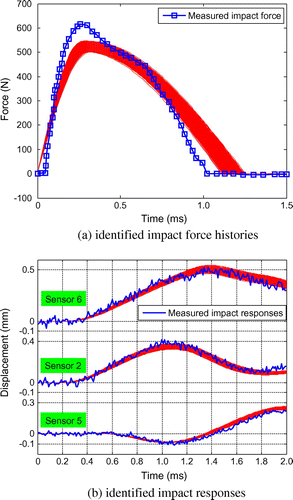
图12.确定肋骨上的冲击力历史，置信区间为90％，测量噪声水平为5％。

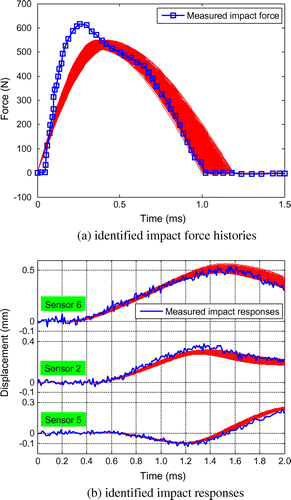
图13.在冲击位置识别出的响应，置信区间为90％，测量噪声水平为5％。

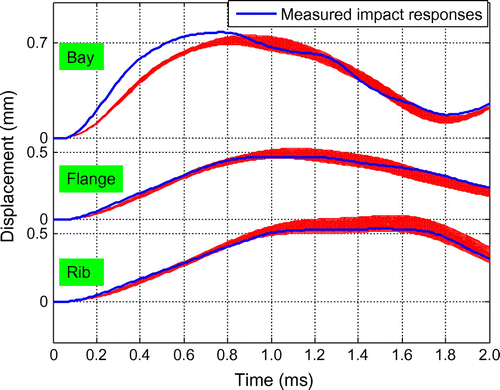
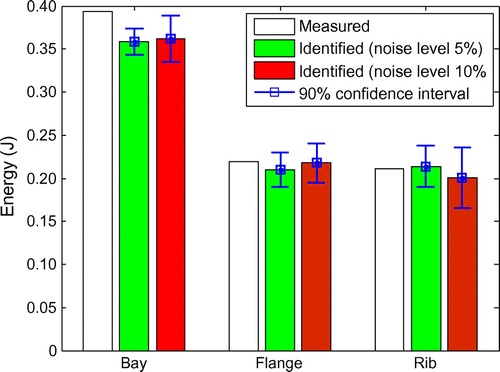
图14.测量和识别的冲击能量的比较。

6。结论

本研究提出了一种统计贝叶斯方法，用于识别加筋复合板上的冲击位置和冲击力历史。首先通过使用一组参数表示冲击载荷将问题转换为参数识别问题。在识别过程中包括表征受到已知冲击载荷的加强复合板的动态响应的前向冲击模型。通过组合测量数据和先验信息，贝叶斯定理用于更新参数的概率分布。特别地，MCMC方法用于对后验分布进行采样以估计影响参数。

转载于:https://www.cnblogs.com/tecdat/p/9481397.html