No free lunch in search and optimization
This article is about mathematical analysis of computing. For associated folklore, see No free lunch theorem.
The problem is to rapidly find a solution among candidates a, b, and c that is as good as any other, where goodness is either 0 or 1. There are eight instances ("lunch plates") fxyz of the problem, where x, y, and z indicate the goodness of a, b, and c, respectively. Procedure ("restaurant") A evaluates candidates in the order a, b, c, and B evaluates candidates in reverse that order, but each "charges" 1 evaluation in 5 cases, 2 evaluations in 2 cases, and 3 evaluations in 1 case.
In computational complexity and optimization the no free lunch theorem is a result that states that for certain types of mathematical problems, the computational cost of finding a solution, averaged over all problems in the class, is the same for any solution method. No solution therefore offers a 'short cut'. In computing, there are circumstances in which the outputs of all procedures solving a particular type of problem are statistically identical. A colourful way of describing such a circumstance, introduced by David Wolpert and William G. Macready in connection with the problems of search[1] and optimization,[2] is to say that there is no free lunch. Wolpert had previously derived no free lunch theorems for machine learning (statistical inference).[3] Before Wolpert's article was published, Cullen Schaffer had summarized a preprint version of this work of Wolpert's, but used different terminology.[4]
In the "no free lunch" metaphor, each "restaurant" (problem-solving procedure) has a "menu" associating each "lunch plate" (problem) with a "price" (the performance of the procedure in solving the problem). The menus of restaurants are identical except in one regard – the prices are shuffled from one restaurant to the next. For an omnivore who is as likely to order each plate as any other, the average cost of lunch does not depend on the choice of restaurant. But a vegan who goes to lunch regularly with a carnivore who seeks economy might pay a high average cost for lunch. To methodically reduce the average cost, one must use advance knowledge of a) what one will order and b) what the order will cost at various restaurants. That is, improvement of performance in problem-solving hinges on using prior information to match procedures to problems.[2][4]
In formal terms, there is no free lunch when the probability distribution on problem instances is such that all problem solvers have identically distributed results. In the case of search, a problem instance is an objective function, and a result is a sequence of values obtained in evaluation of candidate solutions in the domain of the function. For typical interpretations of results, search is an optimization process. There is no free lunch in search if and only if the distribution on objective functions is invariant under permutation of the space of candidate solutions.[5][6][7] This condition does not hold precisely in practice,[6] but an "(almost) no free lunch" theorem suggests that it holds approximately.[8]
Contents
Overview
Some computational problems are solved by searching for good solutions in a space of candidate solutions. A description of how to repeatedly select candidate solutions for evaluation is called a search algorithm. On a particular problem, different search algorithms may obtain different results, but over all problems, they are indistinguishable. It follows that if an algorithm achieves superior results on some problems, it must pay with inferiority on other problems. In this sense there is no free lunch in search.[1] Alternatively, following Schaffer,[4] search performance is conserved. Usually search is interpreted as optimization, and this leads to the observation that there is no free lunch in optimization.[2]
"The 'no free lunch' theorem of Wolpert and Macready," as stated in plain language by Wolpert and Macready themselves, is that "any two algorithms are equivalent when their performance is averaged across all possible problems."[9] The "no free lunch" results indicate that matching algorithms to problems gives higher average performance than does applying a fixed algorithm to all. Igel and Toussaint[6] and English[7] have established a general condition under which there is no free lunch. While it is physically possible, it does not hold precisely.[6] Droste, Jansen, and Wegener have proved a theorem they interpret as indicating that there is "(almost) no free lunch" in practice.[8]
To make matters more concrete, consider an optimization practitioner confronted with a problem. Given some knowledge of how the problem arose, the practitioner may be able to exploit the knowledge in selection of an algorithm that will perform well in solving the problem. If the practitioner does not understand how to exploit the knowledge, or simply has no knowledge, then he or she faces the question of whether some algorithm generally outperforms others on real-world problems. The authors of the "(almost) no free lunch" theorem say that the answer is essentially no, but admit some reservations as to whether the theorem addresses practice.[8]
No free lunch (NFL)
A "problem" is, more formally, an objective function that associates candidate solutions with goodness values. A search algorithm takes an objective function as input and evaluates candidate solutions one-by-one. The output of the algorithm is the sequence of observed goodness values.[10][11]
Wolpert and Macready stipulate that an algorithm never reevaluates a candidate solution, and that algorithm performance is measured on outputs.[2] For simplicity, we disallow randomness in algorithms. Under these conditions, when a search algorithm is run on every possible input, it generates each possible output exactly once.[7] Because performance is measured on the outputs, the algorithms are indistinguishable in how often they achieve particular levels of performance.
Some measures of performance indicate how well search algorithms do at optimization of the objective function. Indeed, there seems to be no interesting application of search algorithms in the class under consideration but to optimization problems. A common performance measure is the least index of the least value in the output sequence. This is the number of evaluations required to minimize the objective function. For some algorithms, the time required to find the minimum is proportional to the number of evaluations.[7]
The original no free lunch (NFL) theorems assume that all objective functions are equally likely to be input to search algorithms.[2] It has since been established that there is NFL if and only if, loosely speaking, "shuffling" objective functions has no impact on their probabilities.[6][7] Although this condition for NFL is physically possible, it has been argued that it certainly does not hold precisely.[6]
The obvious interpretation of "not NFL" is "free lunch," but this is misleading. NFL is a matter of degree, not an all-or-nothing proposition. If the condition for NFL holds approximately, then all algorithms yield approximately the same results over all objective functions.[7] Note also that "not NFL" implies only that algorithms are inequivalent overall by some measure of performance. For a performance measure of interest, algorithms may remain equivalent, or nearly so.[7]
NFL and Kolmogorov randomness
Almost all elements of the set of all possible functions (in the set-theoretic sense of "function") are Kolmogorov random, and hence the NFL theorems apply to a set of functions almost all of which cannot be expressed more compactly than as a lookup table that contains a distinct (and random) entry for each point in the search space. Functions that can be expressed more compactly (for example, by a mathematical expression of reasonable size) are by definition not Kolmogorov random.
Further, within the set of all possible objective functions, levels of goodness are equally represented among candidate solutions, hence good solutions are scattered throughout the space of candidates. Accordingly, a search algorithm will rarely evaluate more than a small fraction of the candidates before locating a very good solution.[11]
Almost all objective functions are of such high Kolmogorov complexity that they cannot arise.[5][7][11] There is more information in the typical objective function or algorithm than Seth Lloyd estimates the observable universe is capable of registering.[12] For instance, if each candidate solution is encoded as a sequence of 300 0's and 1's, and the goodness values are 0 and 1, then most objective functions have Kolmogorov complexity of at least 2300 bits,[13] and this is greater than Lloyd's bound of 1090 ≈ 2299 bits. It follows that not all of "no free lunch" theory applies to physical reality. In a practical sense, algorithms "small enough" for application in physical reality are superior in performance to those that are not. It has also been shown that NFL results apply to incomputable functions [14]
Formal synopsis of NFL
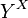is the set of all objective functions f:X→Y, where 
is a finite solution space and 
is a finite poset. The set of all permutations of X is J. A random variable F is distributed on 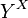. For all j in J, F o j is a random variable distributed on 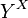, with P(F o j = f) = P(F = f o j−1) for all f in .
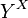Let a(f) denote the output of search algorithm a on input f. If a(F) and b(F) are identically distributed for all search algorithms a and b, then F has an NFL distribution. This condition holds if and only if F and F o j are identically distributed for all j in J.[6][7] In other words, there is no free lunch for search algorithms if and only if the distribution of objective functions is invariant under permutation of the solution space.
The "only if" part was first published by C. Schumacher in his PhD dissertation "Black Box Search – Framework and Methods" (The University of Tennessee, Knoxville (2000)). Set-theoretic NFL theorems have recently been generalized to arbitrary cardinality and .[15]
Original NFL theorems
Wolpert and Macready give two principal NFL theorems, the first regarding objective functions that do not change while search is in progress, and the second regarding objective functions that may change.[2]
Theorem 1: For any pair of algorithms a1 and a2
In essence, this says that when all functions f are equally likely, the probability of observing an arbitrary sequence of m values in the course of search does not depend upon the search algorithm. Theorem 2 establishes a "more subtle" NFL result for time-varying objective functions.
Interpretations of NFL results
A conventional, but not entirely accurate, interpretation of the NFL results is that "a general-purpose universal optimization strategy is theoretically impossible, and the only way one strategy can outperform another is if it is specialized to the specific problem under consideration".[16] Several comments are in order:
A general-purpose almost-universal optimizer exists theoretically. Each search algorithm performs well on almost all objective functions.[11]
An algorithm may outperform another on a problem when neither is specialized to the problem. It may be that both algorithms are among the worst for the problem. Wolpert and Macready have developed a measure of the degree of "match" between an algorithm and a problem.[2] To say that one algorithm matches a problem better than another is not to say that either is specialized to the problem.
In practice, some algorithms reevaluate candidate solutions. The superiority of an algorithm that never reevaluates candidates over another that does on a particular problem may have nothing to do with specialization to the problem.
For almost all objective functions, specialization is essentially accidental. Incompressible, or Kolmogorov random, objective functions have no regularity for an algorithm to exploit. Given an incompressible objective function, there is no basis for choosing one algorithm over another. If a chosen algorithm performs better than most, the result is happenstance.[11] It should be noted that a Kolmogorov random function has no representation smaller than a lookup table that contains a (random) value corresponding to each point in the search space; any function that can be expressed more compactly is, by definition, not Kolmogorov random.
In practice, only highly compressible (far from random) objective functions fit in the storage of computers, and it is not the case that each algorithm performs well on almost all compressible functions. There is generally a performance advantage in incorporating prior knowledge of the problem into the algorithm. While the NFL results constitute, in a strict sense, full employment theorems for optimization professionals, it is important not to take the term literally. For one thing, humans often have little prior knowledge to work with. For another, incorporating prior knowledge does not give much of a performance gain on some problems. Finally, human time is very expensive relative to computer time. There are many cases in which a company would choose to optimize a function slowly with an unmodified computer program rather than rapidly with a human-modified program.
The NFL results do not indicate that it is futile to take "pot shots" at problems with unspecialized algorithms. No one has determined the fraction of practical problems for which an algorithm yields good results rapidly. And there is a practical free lunch, not at all in conflict with theory. Running an implementation of an algorithm on a computer costs very little relative to the cost of human time and the benefit of a good solution. If an algorithm succeeds in finding a satisfactory solution in an acceptable amount of time, a small investment has yielded a big payoff. If the algorithm fails, then little is lost.
Coevolutionary free lunches
Wolpert and Macready have proved that there are free lunches in coevolutionary optimization.[9] Their analysis "covers 'self-play' problems. In these problems, the set of players work together to produce a champion, who then engages one or more antagonists in a subsequent multiplayer game."[9] That is, the objective is to obtain a good player, but without an objective function. The goodness of each player (candidate solution) is assessed by observing how well it plays against others. An algorithm attempts to use players and their quality of play to obtain better players. The player deemed best of all by the algorithm is the champion. Wolpert and Macready have demonstrated that some coevolutionary algorithms are generally superior to other algorithms in quality of champions obtained. Generating a champion through self-play is of interest in evolutionary computation and game theory. The results are inapplicable to coevolution of biological species, which does not yield champions.[9]
Notes
Wolpert, D.H., Macready, W.G. (1995), No Free Lunch Theorems for Search, Technical Report SFI-TR-95-02-010 (Santa Fe Institute).
Wolpert, D.H., Macready, W.G. (1997), "No Free Lunch Theorems for Optimization," IEEE Transactions on Evolutionary Computation 1, 67. http://ti.arc.nasa.gov/m/profile/dhw/papers/78.pdf
Wolpert, David (1996), "“The Lack of A Priori Distinctions between Learning Algorithms," Neural Computation, pp. 1341–1390.
Schaffer, Cullen (1994), "A conservation law for generalization performance," International Conference on Machine Learning, H. Willian and W. Cohen, Editors. San Francisco: Morgan Kaufmann, pp.259–265.
Streeter, M. (2003) "Two Broad Classes of Functions for Which a No Free Lunch Result Does Not Hold," Genetic and Evolutionary Computation – GECCO 2003, pp. 1418–1430.
Igel, C., and Toussaint, M. (2004) "A No-Free-Lunch Theorem for Non-Uniform Distributions of Target Functions," Journal of Mathematical Modelling and Algorithms 3, pp. 313–322.
English, T. (2004) No More Lunch: Analysis of Sequential Search, Proceedings of the 2004 IEEE Congress on Evolutionary Computation, pp. 227–234. http://BoundedTheoretics.com/CEC04.pdf
S. Droste, T. Jansen, and I. Wegener. 2002. "Optimization with randomized search heuristics: the (A)NFL theorem, realistic scenarios, and difficult functions," Theoretical Computer Science, vol. 287, no. 1, pp. 131–144.
Wolpert, D.H., and Macready, W.G. (2005) "Coevolutionary free lunches," IEEE Transactions on Evolutionary Computation, 9(6): 721–735
A search algorithm also outputs the sequence of candidate solutions evaluated, but that output is unused in this article.
English, T. M. 2000. "Optimization Is Easy and Learning Is Hard in the Typical Function," Proceedings of the 2000 Congress on Evolutionary Computation: CEC00, pp. 924–931. http://www.BoundedTheoretics.com/cec2000.pdf
Lloyd, S. (2002) "Computational capacity of the universe," Physical Review Letters 88, pp. 237901–237904. http://arxiv.org/abs/quant-ph/0110141
Li, M., and Vitányi, P. (1997) An Introduction to Kolmogorov Complexity and Its Applications (2nd ed.), New York: Springer.
"Woodward, John R; ",Computable and incomputable functions and search algorithms,"Intelligent Computing and Intelligent Systems, 2009. ICIS 2009. IEEE International Conference on",1,,871-875,2009,IEEE
Rowe, Vose, and Wright, "Reinterpreting No Free Lunch," Evolutionary Computation 17(1): 117–129
Ho, Y.C., Pepyne, D.L. (2002), "Simple Explanation of the No-Free-Lunch Theorem and Its Implications," Journal of Optimization Theory and Applications 115, 549-570.
1507
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
