- 总体的相关系数
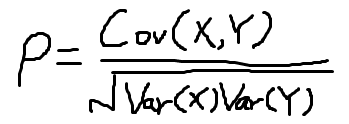
Cov(X,Y):变量 X和 变量Y 的协方差,公式为
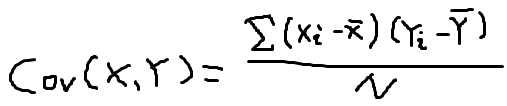
Var(X):变量 X 的方差, Var(X) :
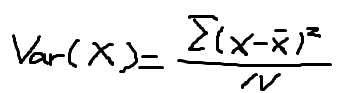
Var(Y):变量 Y 的方差,Var(Y)
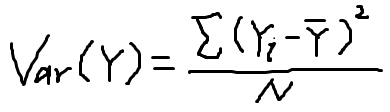
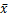 :变量的 X 的平均值
:变量的 X 的平均值
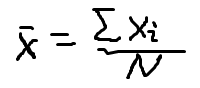
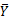 :变量X 的平均值
:变量X 的平均值
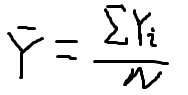
- 样本相关系数
当总体较大时,变量 X 与 Y的全部数值一般不可能去直接观察,从总体中随机抽取一定数量的样本,通过观测值去计算 样本相关系数 r
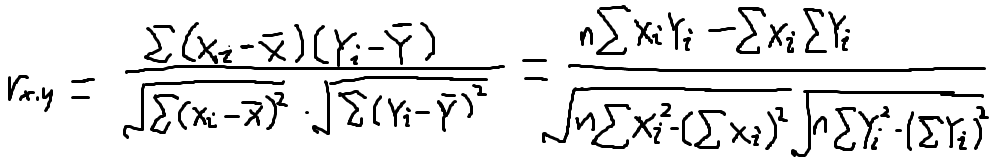
a、样本相关系数作为总体相关系数的估计值
b、涉及的两个变量 X 和 Y地位是平等的
c、相关系数仅能反映两个变量间的线性相关关系
d、相关系数的取值范围
- 相关系数的取值
a、r 的取值范围:-1 <= r <=1
b、r > 0表现正相关, r < 0表示负相关
c、r = 0表示不存在线性相关关系(并不代表无相关,有可能有其他的相关)
d、| r | 表示完全线性相关
e、 0 < | r
| < 1表示存在不同程度线性相关
| r | < 0.3 为微弱线性相关
0.3 <= | r | < 0.5 为低度线性相关
0.5 <= | r | < 0.8 为显著线性相关
0.8 <= | r | < 1 为高度线性相关
- 相关系数的检验
- 为什么要进行检验
r 相关系数是通过样本数据计算的,因而带有一定的随机性
- 检验方法
H0 :
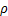 = 0 相关系数在统计上不显著
= 0 相关系数在统计上不显著
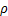 = 0 相关系数在统计上不显著
= 0 相关系数在统计上不显著
H1:
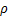 ≠ 0
≠ 0
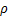 ≠ 0
≠ 0
样本统计量:
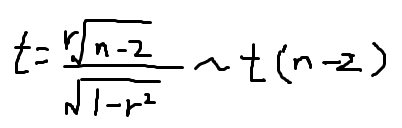

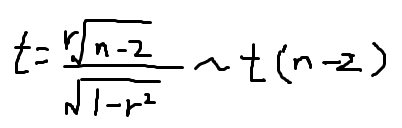
决策:
若 | t | >=
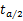 ,表明 r 在统计上是显著的
,表明 r 在统计上是显著的
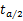 ,表明 r 在统计上是显著的
,表明 r 在统计上是显著的
若 | t | <=
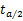 ,表明 r 在统计 上是不显著的
,表明 r 在统计 上是不显著的
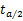 ,表明 r 在统计 上是不显著的
,表明 r 在统计 上是不显著的





 本文介绍了线性相关系数r的概念,包括总体和样本相关系数,并探讨了其在大数据不可直接观测时的计算方法。同时,文章强调了进行相关系数检验的重要性,并概述了检验的流程和目的。
本文介绍了线性相关系数r的概念,包括总体和样本相关系数,并探讨了其在大数据不可直接观测时的计算方法。同时,文章强调了进行相关系数检验的重要性,并概述了检验的流程和目的。

















 4236
4236

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








