课程简单介绍:
接上一节课,这一节课的主题是怎样利用 Regularization 避免 Overfitting。通过给如果集设定一些限制条件从而避免 Overfitting,可是如果限制条件设置的不恰当就会造成 Underfitting。
最后讲述了选择 Regularization 的一些启示式方法。
课程大纲:
1、Regularization
2、Weight decay
3、Choosing a regularizer
1、Regularization
R 有两种方法:
1) Mathematical
函数近似过程的病态问题。
2) Heuristic
妨碍 Ein 的最小化过程。
本节主要介绍另外一种方法。
模型(如果集):Legendre Polynomials + Linear Regression
之所以选择该模型进行解说。是由于该模型可以简化我们的推导。利用其它的模型也可以,可是将会添加推导的难度。对于解说问题。这毫无益处。

通过 Legendre 函数。我们把 x 空间下的数据映射到 Z 空间。
然后就能够利用之前学习过的 Linear Regression 知识进行计算、推导。
以下的思路主要就是在 Hq 的前提下添加一些限制条件。(详细是什么限制条件。详细问题详细分析,然而也有一些指导性原则,因此该限制条件是的设定是 heuristic (启示式)的。比方之前讲过的 H2 和 H10 就是在 H10的模型下添加一些限制条件,从而变成 H2,这叫硬性限制)然后在满足该限制条件的前提下求出最小的 Ein。一般都是用求导 = 0 的方法求得。
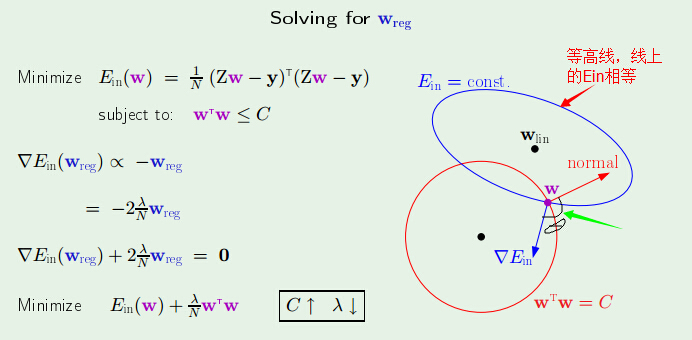
首先先看看在没有设置限定条件的时候,求得的 W 值(Wlin)

在添加限制条件下:为了表述方便。令此时计算得到的 W 为 Wreg

如今的所有问题就是求出 Wreg,在学习其他的方法(如支持向量机,KKT 等)前,以下利用的方法是不严谨的,是基于对图形的分析而得出来的。
红色的圈表示的是限制条件,我们的目的就是在该圈内找到一个W 使得 Ein 最小。
图中的线都是等高线,箭头表示的是最大梯度方向。Wlin表示在没有限制条件的情况下得到的最小的Ein相应的W值。为了得到最小的 Ein,能够不断缩小蓝色圈。使得图中两个圈相切,此时有 Ein 最小。切点就是相应的 W (如果Wlin不包括在红色圈中,否则限制条件也就没有意义了),此时有蓝色箭头和红色箭头在同一条直线上并且方向相反,即 ▽Ein(Wreg) 正比于 -Wreg。
为了方便,我们如果比例系数是:-2λ/N,之所以要加上 常系数是由于这样有利于推导过程的顺利进行,λ 的取值将直接对结果产生影响。
最后一步的最小化结果就是解。(求导 = 0得到的等式跟倒数第二个等式形式一致,这也是为什么要加上那两个常系数的原因),为了方便,令最后一个等式为 Eaug(W),表示添加限制条件下的 Ein。
有了上面的分析,如今问题的求解就非常easy了,例如以下:

当 λ 取不同的值得时候会有不同的表现,当 λ 无限大,则 Wreg = λI,因此无法进行学习。当 λ 变为 0 的时候就退化为没有限制条件下的学习问题。以下看看当 λ 取不同的值对于结果的影响:
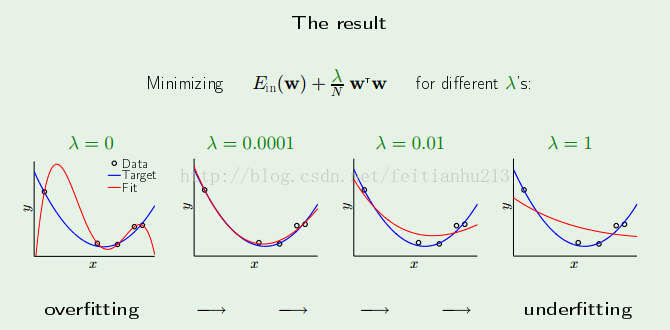
可以看到,假设我们可以找到一个好的 λ 将会对学习结果产生很积极的影响。反之。则会使得学习陷入还有一个极端:Underfitting,根本就把数据给无视了,好人坏人一起干掉!。
因此选取的时候须要小心。
上面对 Eaug的最小化过程叫做 Weight decay。why?
2、Weight decay
在神经网络中有类似以下的公式:
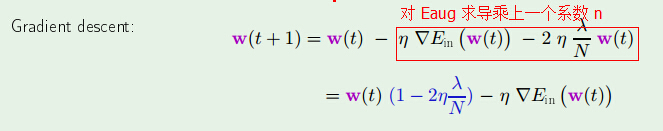
当 λ 非常小的时候,其效果相当于降低 W(t)。因此叫做 decay。但是。为什么一定要降低?假设添加会如何?依照经验,假设添加 W(t) 会使得结果变得糟糕,例如以下图:
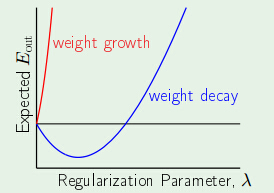
在这样的情况下,仅仅有当 λ 等于 0 的时候才干最小化 Eout,此时相当于没有限制条件。当然,这些仅仅是一些指导性的规则,并没有严格的数学限制。事实上机器学习非常多时候都是这样,基于一个如果,然后进行学习。学习的效果跟如果有非常大的关系。或者说如果的好坏直接影响到机器学习的效果。
其实,我们的限制条件能够是多样的,比方。我们能够在上述的限制条件下添加一些參数,使得对于不同项的系数拥有不同的限制条件:
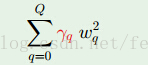
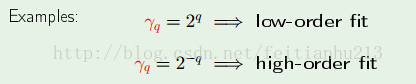

一般化:
令
Ω =
Ω(h),当中
Ω 表示Regularizer。通过
Ω 对如果集添加限制条件。
如今就是要最小化:Eaug(h) = Ein(h) + λ/
N*
Ω(h)
上面的公式跟:
Eout(h) <= Ein(h) + Ω(H) 非常相似。
曾经我们把 Ein 作为 Eout 的一个代理。如今Eaug将更好的完毕这项工作。
如今问题是该怎样得到 Ω ?
3、Choosing a regularizer
Ω 的选取是一个启示性的问题。通过对实际的观察,我们得到例如以下实践的规则:
1) 随机噪声一般都是高频的,尖锐的。
2) 确定性噪声一般也不是平滑的。
因此我们限制的一般化原则是使得学习的结果想着平滑、简洁的方向进行。
最后,我们看看 λ 对结果的影响:
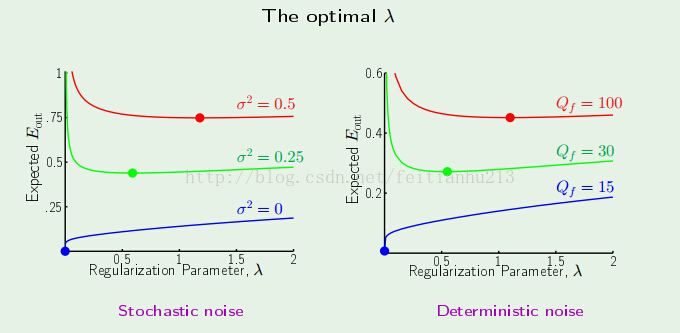
























 728
728

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








