链表相关的面试题型总结及其个别实现
对指针的掌握程度,是衡量一个程序员的基本功是否扎实的重要考量标准。而数据结构中的链表、二叉树等基本数据结构,是考核指针的最佳利器。本文稍微总结了下链表的主要考点,以备未来的求职。
说在前面的注意事项
首先,涉及到指针的编程,对于指针有效性的判断不可忽视,代码中一定要有对NULL指针的判断,这样代码才更加的鲁棒。
其次,若对链表进行插入,删除操作,一定要注意更新head指针(和tail指针)的指向。
最后,我们定义结点的数据结构为:
struct Node{
int datum;
Node * next;
};
int datum;
Node * next;
};
先总结下我的心得
首先,若是题目对空间复杂度没有什么要求,可以借鉴hash,额外的数组等,将问题简化
其次,可以使用快慢指针的思想,设置两个指针,一个指针走得快些或先走几步,就能够很好的解决大多数问题。
再者,对于指针的访问操作,一定要小心再小心,一定要确认有效才能继续访问。
最后,涉及到修改头指针指向的操作(插入,删除,排序等),函数中传入的指针参数要设置成 Node**, 这样才能进行修改操作。
常考的题型
对于链表, 主要考核以下几类部分:
一、查询判断类
- 判断两链表是否相交, 若相交,返回第一个相交结点
- 判断链表是否有环
- 求链表的倒数第 K 个数
二、操作类
- 链表排序
- 链表插入
- 链表删除结点
- 若给定欲删除的结点指针,如何在O(1)时间内删除?
- 有序链表合并
- 复杂链表复制
问题分析及求解
1.1. 两链表(无环)相交的判定


思路一:
尾地址判定法。常规的判断方法是判断两链表的
最后一个结点地址是否相同。具体做法是先遍历list1, 保存最后一个结点的地址end1;再遍历list2到最后一个结点,判断地址是否等于end1。 时间复杂度为O(len1+len2), 空间复杂度为 O(1)。

 View Code
View Code


1 bool cross_tail_compare(Node* h1, Node* h2) 2 { 3 if(h1 == NULL || h2 == NULL){ 4 return NULL; 5 } 6 Node* p = h1; 7 while(p->next!=NULL){ 8 p = p->next; 9 } 10 Node* q = h2; 11 while(q->next!=NULL){ 12 q = q->next; 13 } 14 return (p == q); 15 }
思路二:
hash地址法。通常若允许使用hash的话,能够快速有效的解决。 这里,我们遍历list1, 将每个结点的地址hash;再遍历list2,判断结点地址是否出现在hash表中。时间复杂度为O(len1+len2), 空间复杂度为O(len1); 这里,虽然时间复杂度未降低,同时增加了空间复杂度,但是却能很好的解决第1个公共结点问题。算是一种补偿。
思路三:
链接成环法。参考下面图3。首先,先将第一个链表的最后一个结点链接到第二个结点的头,然后判断是否有环,若有环,则说明两个链表存在公共结点。
1.2. 链表是否有环的判定
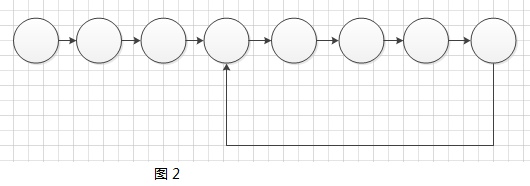
思路一:
快慢指针法. 我们在用快fast, slow两指针指向链表头,fast指针一次跨两步, slow指针一次跨一步,有环的条件为fast==slow != NULL 。

 View Code
View Code


1 Node* fastinCircle(Node* head) 2 { 3 if(head == NULL) 4 return NULL; 5 Node* fast = head; 6 Node* slow = head; 7 while((fast!=NULL) && (fast->next != NULL) && (slow!=NULL)){ 8 fast = fast->next->next; 9 slow = slow->next; 10 if(fast == slow) break; 11 } 12 if((fast == NULL) || (fast->next == NULL) || (fast != slow)) return NULL; 13 return fast; 14 }
思路二:
hash地址法。遍历链表,将地址hash进来,若NULL了,则说明无环,若存在相同的地址,则说明有环。 且能得到第一个入环的点。时间复杂度为O(len1), 空间复杂度为O(len1)。
1.3. 寻找两链表的第一个公共结点
思路一:
hash地址法。通过1.1的分析,我们能够用hash的方法快速得到第一个公共的结点。
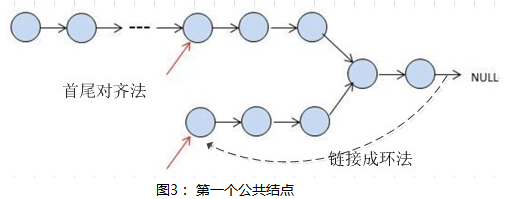
思路二:
首尾对齐法。若采用尾地址判定法,我们能够得到最后一个公共结点,那么回溯N步同时判断地址是否相等,就能得到第一个公共结点了。可惜是单链表,没有prev指针,但是这个思想启发了我们,若是两个链表尾对齐了,那么对长链表先next X 步,使头部也对齐,那么,第一个相同的地址点,就是第一个公共结点了。根据 图3, 我们可以看出,长链表先走X=(lenMax-lenMin)步后,那么,他们将同时递增到first common 点。时间复杂度为O(len1+len2+x), 空间复杂度为O(1)。
Node* cross_first(Node* h1, Node* h2) { if(h1==NULL || h2==NULL){ return NULL; } Node* p = h1; int s1 = 0; while(p->next != NULL){ ++s1; p = p->next; } Node* q = h2; int s2 = 0; while(q->next != NULL){ ++s2; q = q->next; } if(p != q) return NULL; p = h1; q = h2; int prestep = static_cast<int>(abs(s1-s2)); if(s1>s2){ while(prestep--){ p = p->next; } }else{ while(prestep--){ q = q->next; } } while(p != q){ p = p->next; q = q->next; } return p; }
思路三:
链接成环法(也是求环的入口点的解法)。将链表1的尾结点链接到链表2的第一个结点,然后调用快慢指针法判断是否有环。然后保存相遇点,同时slow指针从头开始,步长为1递增;fast指针从相遇点开始,步长为1递增,他们再一次的相遇点,则是第一个公共结点。
数学推导如下:
先假设链表长 L, 入环前结点数 b, 环内结点 r, slow指针走了 s 步相遇, 相遇点为环内 x 步, 则 fast 指针走了 2s 步, 且相遇点前fast已近走了n(n>=1) 圈。 则有:
s
+nr
=
2s
s = nr
s = b + x
r = L - b;
b + x = nr = (n - 1)r +r = (n - 1)r + L - b
b = (n - 1)r + L-b-x
s = nr
s = b + x
r = L - b;
b + x = nr = (n - 1)r +r = (n - 1)r + L - b
b = (n - 1)r + L-b-x
这里,L-b-x 等于相遇点到环结尾的长度,b 为开头到环入口的长度。因此,在链表头和相遇点各设置一个指针,继续走 b 步,就肯定能相遇。
Node* cross_first_by_circle(Node* h1, Node* h2) { if(h1 == NULL || h2 == NULL) return NULL; Node* p = h1; while(p->next != NULL){ p = p->next; } Node* holdh1 = p; p->next = h2; Node* fast = NULL; fast = fastinCircle(h1); if(fast == NULL) return NULL; Node* slow = h1; while(fast != slow){ fast = fast->next; slow = slow->next; } p->next = NULL; return fast; }
参考资料:
《剑指offer》
1.4 求链表的倒数第K个数
有了前面
首尾对齐法和
快慢指针的思想,我们是不是能启发到怎么求倒数第K个数呢?
思路一: 若是双向链表,则很简单,从尾端往回走K步就行。
思路二: 若是单链表,先遍历得到链表的长度,然后逆推出要到倒数k位置,则要走 n-k+1步;
思路三:
很简单,设置两个指针,一个指针从从头先走k-1步,另外个指针再从头开始,那么,当第一个指针到达结尾时,另外个指针恰好到达倒数第K个结点。
Node* backK(Node* head, int k) { if(head == NULL || k <= 0) return NULL; Node* p = head; for(int i=0; i<k-1; ++i){ if(p->next == NULL) return NULL; p = p->next; } Node* knode = head; while(p->next != NULL){ p = p->next; knode = knode->next; } return knode; }
归纳法证明:
若k=1: k-1 = 0, 两个指针同步运行,成立。
若k=x; k-1 = x-1; 第一个指针继续走 n-x步到达最后一个结点, 第二个指针走 (n-x) 步后,处于倒数 n-(n-x)=x 的位置,成立。
这里的注意事项是: 若链表长度小于k怎么办? 输入的是空链表怎么办?若输入k=0, 则k-1步导致溢出怎么办?因此,写好一个好的代码是要考虑很多因素的。
2.1 链表排序
对链表排序,想下似乎挺简单的,实际上是很富有挑战性的。这里我们以单链表为例。
思路一: 若是空间非常富裕的话,我们完全可以借鉴STL中对deque进行排序时候的做法,先将元素赋值到vector中,排序后再拷贝回deque。 做法也是一样的,遍历链表,把每个元素存入到一个新的数组中,然后对该数组排序(默认使用快排),然后再拷贝回链表(只修改卫星数据)。时间复杂度为O(n+
nlgn+n) = O(nlgn), 空间复杂度为O(n);
思路二: 单链表,只能前向移动,我们考虑到简单的排序方法必须是相邻进行比较的,符合条件的有插入排序,冒泡排序,甚至,希尔排序也是可以的。同时,排序算法内部的循环也必须是前向移动才行。
对于思路二,我们有两种想法,交换指针or交换数据域。
我们先做下简单的,不交换指针,只交换卫星数据,这样,代码就很容易实现。 下面代码实现了冒泡排序和插入排序。和常规的解法不同的是,内循环是头比到尾的,同时采用了STL的[ ) 方式来实现,NULL真是个好哨兵呀。
对于思路二,我们有两种想法,交换指针or交换数据域。
我们先做下简单的,不交换指针,只交换卫星数据,这样,代码就很容易实现。 下面代码实现了冒泡排序和插入排序。和常规的解法不同的是,内循环是头比到尾的,同时采用了STL的[ ) 方式来实现,NULL真是个好哨兵呀。
1 void insert_sort(Node* head,Node* end = NULL) // 插入排序 2 { 3 if (head == end) return; 4 Node* piot = head->next; // 每次要比较的主元 5 Node* cur = head; 6 int tmp; 7 while(piot != end){ 8 cur = head; // 每次都从头开始 9 while( (cur!=piot) && (cur->datum<=piot->datum)){ // 插入的合适位置 10 cur = cur->next; 11 } 12 tmp = cur->datum; // 交换卫星数据域 13 cur->datum = piot->datum; 14 piot->datum = tmp; 15 piot = piot->next; // 主元指向下一个 16 } 17 } 18 19 void bubble_sort(Node* head, Node* end = NULL) // 冒泡排序 20 { 21 if(head == end) return; 22 Node* piot = head; // 23 Node* cur; 24 Node* prev; 25 int tmp; 26 bool change = true; 27 while(piot != end){ // 外层主循环 28 cur = piot->next; // 当前 29 prev = piot; // 前一个 30 change = false; 31 while(cur != end){ 32 if(cur->datum < prev->datum){ // 逆序则交换 33 tmp = cur->datum; 34 cur->datum = prev->datum; 35 prev->datum = tmp; 36 change = true; 37 } 38 prev = cur; 39 cur = cur->next; 40 } 41 piot = piot->next; 42 if( !change ) break; 43 } 44 }
对于交换指针来说,想下是好恐怖的一件事呀。其实不难,把结点交换的函数抽取出来,问题就简单了
首先,我们要设计一下链表节点的交换函数 swap_point, 这个函数的声明如下:
1 void swap_point(Node** head, // 链表的头指针地址 2 Node* preFirst, Node* first, // preFirst: 与交换的第一个指针前一个结点; first: 交换的第一个结点 3 Node* preSecond, Node* second) // // preSecond: 与交换的第二个指针前一个结点; second: 交换的第二个结点
然后,要考虑两大种情况的组合:
- first 是否为头结点?
- first->next 是否等于 second ?
对于头结点问题,我们知道这是链表问题必须考虑的,我们在代码中加个判断语句,选择性执行头结点的更新就行。
对于first->next 是否等于 second ,大家画图下,就很好理解了:


接着,我们在插入排序中,在要交换的位置传入合适的前向指针,就行,哈哈,代码如下:
1 void swap_point(Node** head, Node* preFirst, Node* first, Node* preSecond, Node* second) 2 { 3 if(head == NULL || *head == NULL || first == NULL || second == NULL) return ; 4 if(first->next != second){ 5 Node* tmp = first->next; 6 first->next = second->next; 7 second->next = tmp; 8 preSecond->next = first; 9 }else{ 10 first->next = second->next; 11 second->next = first; 12 } 13 if(*head != first) 14 preFirst->next = second; 15 else 16 *head = second; 17 } 18 19 void insert_sort_point(Node** head, Node* end = NULL) 20 { 21 if(*head == end) return; 22 Node* piot = (*head)->next; 23 Node* prepiot = *head; 24 Node* cur = *head; 25 Node* precur = *head; 26 while(piot != end){ 27 cur = *head; 28 while((cur != piot) && (cur->datum<=piot->datum)){ 29 precur = cur; 30 cur = cur->next; 31 } 32 swap_point (head, precur, cur, prepiot, piot); 33 prepiot = piot; 34 piot = piot->next; 35 } 36 }

经过测试,成立!
2.2 链表插入
对于链表插入操作,分为头插法和尾插法。 若是排序好的链表插入,还要定位到相应的位置。
1 Node* insert_front(Node** head, int value) 2 { 3 if(head == NULL) 4 return NULL; 5 if(*head == NULL){ 6 *head = new Node(value); 7 }else{ 8 Node* p = new Node(value); 9 p->next = *head; 10 *head = p; 11 } 12 return *head; 13 } 14 Node* insert_comp(Node** head, int value) 15 { 16 if (head == NULL) 17 return NULL; 18 Node* in; 19 if (*head == NULL) { 20 in = new Node(value); 21 *head = in; 22 }else{ 23 in = new Node(value); 24 if((*head)->datum > value){ 25 insert_front (head, value); 26 }else{ 27 Node* p = *head; 28 Node* n = (*head)->next; 29 while( n != NULL && n->datum < value){ 30 p = n; 31 n = n->next; 32 } 33 p->next = in; 34 in->next = n; 35 } 36 } 37 return in; 38 }
2.3 链表删除某一节点
对于删除操作,简单的来说,就是两个指针,一前一后,后的一个到达删除点后,操作就很简单了。还有个方法,见2.4.
2.4 单位时间内删除节点(节点指针给定)
对于这个,一般通常的做法是采用2.3的做法,但是这个时间复杂度为O(n)。 可以参考下<剑指offer>中介绍的方法,我们先画图来说下:

图4的上半部分是我们通常(2.3)的做法,需要前一个指针辅助删除;
图4下半部分的删除,就不需要了。做法如下:
首先来个辅助指针q指向下一个结点。 将q的数据域赋给cur, 然后更新cur.next, 最后删除q。 这样,就能在O(1)的时间内删除结点了。
1 void delNode(Node** head, Node* n) 2 { 3 if(head == NULL || *head == NULL || n == NULL) 4 return; 5 if(n->next != NULL){ // 删除的不是尾结点; 6 Node* tmp = n->next; 7 n->datum = tmp->datum; 8 n->next = tmp->next; 9 delete tmp; 10 tmp = NULL; 11 }else if(*head == n){ // 仅有一个结点 12 delete n; 13 *head = NULL; 14 }else{ // 删除尾结点 15 Node* p = *head; 16 while(p->next != n){ 17 p = p->next; 18 } 19 p->next = NULL; 20 delete n; 21 n = NULL; 22 } 23 }
2.5 有序链表合并
这个可以参考下STL中的接合函数的写法。
2.6 复杂链表复制
参考下<剑指offer>
测试函数:

 打印函数
打印函数
测试函数:


1 void show(const Node* head, const Node* end = NULL) 2 { 3 if(head == end) return; 4 const Node* p = head; 5 while(p != end){ 6 cout << p->datum << "-->" ; 7 p = p->next; 8 } 9 if(end == NULL) 10 cout << "NULL" << endl; 11 else{ 12 cout << end->datum << endl; 13 } 14 }
1 #include "myslist.h" 2 #include <iostream> 3 using namespace std; 4 int main() 5 { 6 Node* head1 = NULL; 7 insert_comp (&head1, 1); 8 insert_comp (&head1, 2); 9 insert_comp (&head1, 3); 10 insert_comp (&head1, 7); 11 insert_comp (&head1, 15); 12 Node* head2 = insert_comp (&head1,6); 13 insert_front(&head2,5); 14 insert_front(&head2,4); 15 show(head1); 16 show(head2); 17 cout << "Is cross? " << cross_tail_compare (head1,head2) << endl; 18 cout << "The first cross point by cross_first: " << cross_first (head1,head2)->datum << endl; 19 cout << "The first cross point by cross_first_circle: " << cross_first_by_circle (head1,head2)->datum << endl; 20 cout << "back 5's node of head1 is: " << backK (head1,5)->datum << endl; 21 Node* pp = fastinCircle (head2); 22 if(pp == NULL){ 23 cout << "No circle" << endl; 24 }else{ 25 cout << "circle" << endl; 26 } 27 cout << "-----------Test Circle---------------" << endl; 28 Node* head3 = NULL; 29 insert_comp (&head3, 1); 30 insert_comp (&head3, 2); 31 Node* circin = insert_comp (&head3, 3); 32 insert_comp (&head3, 7); 33 Node* tail = insert_comp (&head3, 15); 34 tail->next = circin; 35 show(head3,tail); 36 show(tail,tail->next); 37 pp = fastinCircle(head3); 38 if(pp == NULL){ 39 cout << "No circle" << endl; 40 }else{ 41 cout << "circle" << endl; 42 } 43 return 0; 44 }






















 485
485

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








