HDU 4686 Arc of Dream（递归矩阵加速）

标题效果：你就是给你一程了两个递推公式公式，第一个让你找到n结果项目。

注意需要占用该公式的复发和再构造矩阵。

Arc of Dream

Time Limit: 2000/2000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 2092    Accepted Submission(s): 664

Problem Description

An Arc of Dream is a curve defined by following function:

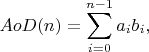
where
a ₀ = A0
a _i = a _i-1*AX+AY
b ₀ = B0
b _i = b _i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?

 

Input

There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 ¹⁸, and all the other integers are no more than 2×10 ⁹.

 

Output

For each test case, output AoD(N) modulo 1,000,000,007.

 

Sample Input

1 1 2 3 4 5 6 2 1 2 3 4 5 6 3 1 2 3 4 5 6

 

Sample Output

4 134 1902

 

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define eps 1e-10
///#define M 1000100
#define LL __int64
///#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?

0:x) #define mod 1000000007 const int maxn = 210; using namespace std; struct matrix { LL f[10][10]; }; matrix mul(matrix a, matrix b, int n) { matrix c; memset(c.f, 0, sizeof(c.f)); for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { for(int k = 0; k < n; k++) c.f[i][j] += a.f[i][k]*b.f[k][j]; c.f[i][j] %= mod; } } return c; } matrix pow_mod(matrix a, LL b, int n) { matrix s; memset(s.f, 0 , sizeof(s.f)); for(int i = 0; i < n; i++) s.f[i][i] = 1LL; while(b) { if(b&1) s = mul(s, a, n); a = mul(a, a, n); b >>= 1; } return s; } matrix Add(matrix a,matrix b, int n) { matrix c; for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { c.f[i][j] = a.f[i][j]+b.f[i][j]; c.f[i][j] %= mod; } } return c; } int main() { LL n; LL a, ax, ay; LL b, bx, by; while(~scanf("%I64d",&n)) { scanf("%I64d %I64d %I64d",&a, &ax, &ay); scanf("%I64d %I64d %I64d",&b, &bx, &by); a %= mod; ax %= mod; ay %= mod; b %= mod; bx %= mod; by %= mod; LL ff = a*b%mod; LL x = (a*ax+ay)%mod; LL y = (b*bx+by)%mod; LL pp = (x*y)%mod; if(n == 0) { puts("0"); continue; } matrix c; memset(c.f, 0 ,sizeof(c.f)); c.f[0][0] = ax*bx%mod; c.f[0][1] = ax*by%mod; c.f[0][2] = ay*bx%mod; c.f[0][3] = ay*by%mod; ///c.f[0][4] = 1LL; c.f[1][1] = ax; c.f[1][3] = ay; c.f[2][2] = bx; c.f[2][3] = by; c.f[3][3] = 1LL; c.f[4][0] = 1LL; c.f[4][4] = 1LL; matrix d = pow_mod(c, n-1LL, 5); LL sum = 0LL; sum += ((d.f[4][0]*pp%mod)+(d.f[4][4]*ff%mod))%mod; sum += ((d.f[4][1]*x%mod) + (d.f[4][2]*y%mod) + d.f[4][3]%mod)%mod; printf("%I64d\n",(sum+mod)%mod); } return 0; }

版权声明：本文博客原创文章，博客，未经同意，不得转载。