java实现Floyd算法求最短路径

最新推荐文章于 2024-09-03 19:17:12 发布

weixin_34112181

最新推荐文章于 2024-09-03 19:17:12 发布

阅读量250

点赞数 2

文章标签： java 数据结构与算法 python

原文链接：https://my.oschina.net/u/1247611/blog/159952

版权

2019独角兽企业重金招聘Python工程师标准>>>

关于无向图的最短路径问题：

这个程序输出：最短路径矩阵

例如:W[0][5]=9 代表vo->v5的最短路径为9

W=:

0 1 3 7 4 9

1 0 2 6 3 8

3 2 0 4 1 6

7 6 4 0 3 2

4 3 1 3 0 5

9 8 6 2 5 0

package com.xh.Floyd;  
import java.util.ArrayList;  

public class Floyd_01 {  
	public static int M = Integer.MAX_VALUE;     
	public static int MAXSUM(int a,int b){      
		return (a!=M&&b!=M)?(a+b):M;     
	} 
    public static ArrayList<Integer[][]> flody(Integer[][] dist){
       	Integer[][] path=new Integer[6][6];//存储的是从i->j经过的最后一个节点     
       	for (int i = 0; i < 6; i++) {     
	        for (int j = 0; j < 6; j++) {
	            path[i][j]=i; 
                } 
	    } 
        for(int k=0;k<6;k++){
            for (int i = 0; i < 6; i++) {
                for (int j = 0; j < 6; j++) {
		            if(dist[i][j]>MAXSUM(dist[i][k], dist[k][j])){   
    					path[i][j]=path[k][j];//存储的是从i->j经过的最后一个节点        
						dist[i][j]=MAXSUM(dist[i][k], dist[k][j]);    
					} 
				} 
			} 
        }                    
        ArrayList<Integer[][]> list =new ArrayList<Integer[][]>();          
		list.add(dist);
		list.add(path);         
		return list;     
	} 
    public static Integer[] reverse(Integer[] chain,int count){
        int temp; 
     	for(int i=0,j=count-1;i<j;i++,j--){
	       temp=chain[i];
	       chain[i]=chain[j];
	       chain[j]=temp; 
     	} 
     	return chain;     
	} 
    public static void display_path(ArrayList<Integer[][]> list){
	    Integer[][] dist=list.get(0);      
		Integer[][] path=list.get(1);      
		Integer[] chain=new Integer[6]; 
     	System.out.println("orign->dist"+" dist "+" path");
        for (int i = 0; i <6; i++) {
		    for (int j = 0; j < 6; j++) {
			    if(i!=j){//只是避免了vi->vi的输出
					//输出源到目的地 
	     			System.out.print("\n   "+(i)+"->"+(j)+"     ");      
					//输出最短路径的长度      
					if(dist[i][j]==M){       
						System.out.print(" NA "); 
	     			}else{ 
	      				System.out.print(dist[i][j]+"      ");       
						int count=0;       
						int k=j;       
						do {        
							k=chain[count++]=path[i][k];       
						} while (i!=k); 
	      				chain=reverse(chain,count);        
	      				//输出路径 
	      				System.out.print(chain[0]+"");  
						for(k=1;k<count;k++){ 
							System.out.print("->"+(chain[k])); 
	      				} 
	      				System.out.print("->"+j); 
	     			} 
    			} 
   			} 
		} 
    } 
 	public static void main(String[] args) {   
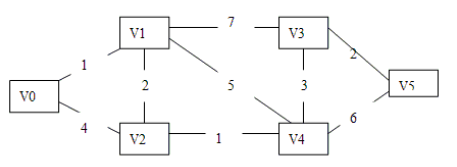
        Integer[][] dist = {     
				{ 0, 1, 4, M, M, M },     
				{ 1, 0, 2, 7, 5, M },     
				{ 4, 2, 0, M, 1, M },     
				{ M, 7, M, 0, 3, 2 },     
				{ M, 5, 1, 3, 0, 6 },  
				{ M, M, M, 2, 6, 0 } };// 建立一个权值矩阵 

		ArrayList<Integer[][]>  list=flody(dist); 
        display_path(list);                   
	} 
}

转载于:https://my.oschina.net/u/1247611/blog/159952