图的邻接矩阵存储结构

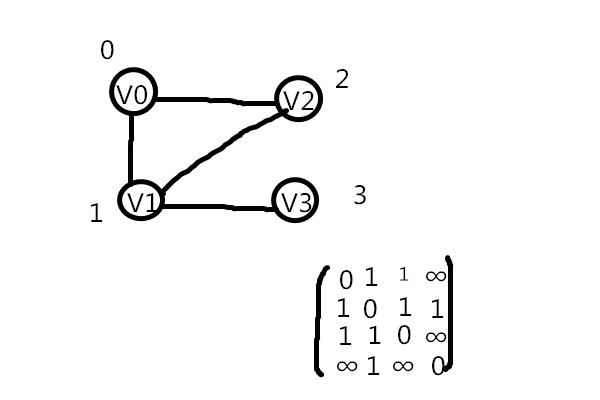
如上图，我们能够把v0标记为0，v1标记为1。。。。

并把联通的2点权值全设置为1，那么能够用邻接矩阵（右图）来表示

概念解析：

第一个邻接顶点：

我们以vo为例，第一个邻接顶点为V1（事实上也能够使V3，仅仅只是考虑计算机的存储顺序。我们找邻接顶点，通常是从v0扫描到v3，所以我们先在内存中扫描到v1）

下一个邻接顶点：

我们以v0为例。下一个邻接顶点就是v3（相同。事实上也能够使V1，仅仅只是考虑计算机的存储顺序。我们找下个邻接顶点，通常是从v2扫描到v3，之所以从v2扫描起，那是由于，V1已经是第一个邻接顶点了。那么下一个邻接顶点一定是在内存中存储在V1后的数据了）

无向图邻接矩阵的特点：

对角线权值是0

无向图矩阵关于斜线对称（有向图不正确称）

代码例如以下：

#include<iostream>
using namespace std;
#define VertexSize 10
typedef struct
{
	int weight[VertexSize][VertexSize];  //表示2个顶点之间的权值
	int edgenum; //表示图的边数目
}Graph;

//初始化图
void Initiate_Graph(Graph *g,int n)
{
	int i,j;
	g->edgenum=0;
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
		{
			if(i==j) g->weight[i][j]=0;  //对角线表示顶点自己到自己。权值为0
			else g->weight[i][j]=0x7fff; //其它权值初始化为无限大
		}
}

//插入边
void InsertEdge(Graph *g,int v,int w,int weight,int n)
{
	if(v<0 || v>=n||w<0||w>=n)
	{
		cout<<"overflow!"<<endl;
	}
	g->weight[v][w]=weight;
	g->edgenum++;
}

//取得点V的第一个临接顶点
int GetFirstVertex(Graph *g,int v,int n)
{
	if(v<0||v>=n)
	{
		cout<<"overflow"<<endl;
		return -1;
	}
	int i;
	for(i=0;i<n;i++)
	{
		if(( (g->weight[v][i])>0 )&&( (g->weight[v][i])<0x7fff) )
			return i;
	}
	return -1;

}

//取得顶v的下一个邻接顶点
int GetNextVertex(Graph *g,int v,int w,int n)
{
	if(v<0||v>=n||w<0||w>=n)
	{
		cout<<"overflow"<<endl;
		return -1;
	}
	int i;
	for(i=w+1;i<n;i++)
	{
		if( ((g->weight[v][i])>0 )&& ((g->weight[v][i])<0x7fff ))
			return  i;
	}
	return -1;
}

//删除边
void DeleteEdge(Graph *g,int v,int w,int n)
{
	if(v<0||v>=n||w<0||w>=n||v==w)
	{
		cout<<"error"<<endl;
	}
	g->weight[v][w]=0x7fff;
	g->edgenum--;
}


void PrintGraph(Graph *g,int n)
{
	int y,x,i;
	for(i=0;i<n;i++)
	{
		y=GetFirstVertex(g,i,n);
		if(y==-1)
		{
			cout<<"Vertex:"<<i<<"没有第一个邻接顶点"<<endl;
		}
		else
		{
			cout<<"Vertex:"<<i<<"第一个邻接顶点"<<y<<endl;
			x=GetNextVertex(g,i,y,n);
			if(x!=-1)
			{
				cout<<"Vertex:"<<i<<"下一个邻接顶点"<<x<<endl;
			}
			else
			{
				cout<<"Vertex:"<<i<<"没有第二个邻接顶点"<<endl;
			}
		}
	}
}

void main()
{
	Graph g;
	int n,edge;
	cout<<"请输入图的顶点个数:"<<endl;
	cin>>n;
	cout<<"请输入图的边个数"<<endl;
	cin>>edge;
	Initiate_Graph(&g,n);
	int i,p1,p2,weight;
	cout<<"请输入顶点-顶点-权值:"<<endl;
	for(i=0;i<edge;i++)
	{
		cin>>p1>>p2>>weight;
		InsertEdge(&g,p1,p2,weight,n);
	}
	PrintGraph(&g,n);
	cout<<"输入须要删除的边："<<endl;
	int e1,e2;
	cin>>e1>>e2;
	DeleteEdge(&g,e1,e2,n);
	cout<<"删除后边的数目为："<<g.edgenum<<endl;
	system("pause");
}