概率论与随机过程

2019独角兽企业重金招聘Python工程师标准>>>

一、概率分布(probability distribution)

概率分布是概率论的基本概念之一，用以表述随机变量取值的概率规律。

概率密度函数：一个连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值在（某一个确定的取值点）附近的可能性的函数。而随机变量的取值落在（某个区域之内的概率）则是概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

在相同条件下进行n次重复试验，如果随机事件A发生的次数为m，那么m/n称为随机事件A的频率（frequency）；当试验重复数n逐渐增大时，随机事件A的频率越来越稳定地接近某一数值p，那么就把p称为随机事件A的概率。这样定义的概率称为统计概率（statistics probability），或者称后验概率（posterior probability）

1、离散型随机变量概率分布

（1）两点分布

若一个随机变量X只有两个可能取值，其分布为P{X=x1}=p,P{X=x2}=1-p(0<p<1)

（2）二项分布（Binomial Distribution，Bernoulli Experiment）

二项分布是n个独立的是/非试验中成功的次数的离散概率分布。 重复n次的伯努利试验。在每次试验中只有两种可能的结果，而且是互相对立的，是独立的，与其它各次试验结果无关，结果事件发生的概率在整个系列试验中保持不变，则这一系列试验称为伯努力试验。

P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k), 其中C(n, k) = n!/(k! * (n-k)!)；

记作ξ~B(n,p) 期望：Eξ=np 方差:Dξ=npq

（3）泊松分布 若随机变量x服从参数为λ的指数分布，则记为 X~ P(λ). 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率（泊松分布适合于描述单位时间（或空间）内随机事件发生的次数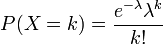）。 其数学期望与方差相等，同为参数λ： E(X)=V(X)=λ

2、连续型随机变量概率分布

（1）指数分布：

是一种连续概率分布，可以用来表示 概率密度函数： 若随机变量x服从参数为λ的指数分布，则记为 X~ e(λ).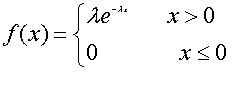

累积概率分布：

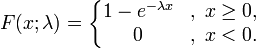
期望：

方差：

【指数分布和泊松分布】：

如果单位时间事件发生的次数服从参数为r的泊松分布，泊松事件流的等待时间，则任连续发生的两次时间的间隔时间序列服从参数为r的指数分布!

（2）正态分布

三、马尔可夫过程

1、马尔可夫性，又无后效性

按参数空间与状态空间分，离散参数集，离散状态集的马尔可夫过程，称为马尔可夫链； 利用马尔可夫过程分析系统当前状态并预测未来状态的决策方法，称为马尔可夫决策；

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个（含有隐含未知参数）的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。

假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什么.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况. 你认为天气的运行就像一个马尔可夫链.其有两个状态 "雨"和"晴",但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的概率进行下列活动:"散步", "购物", 或 "清理". 因为你朋友告诉你他的活动,所以这些活动就是你的观察数据.这整个系统就是一个隐马尔可夫模型HMM. http://zh.wikipedia.org/wiki/%E9%9A%90%E5%90%AB%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E6%A8%A1%E5%9E%8B

2、转移概率、转移概率矩阵 定义：称P{X m+n=j|Xm=i}为马氏链在m时刻处于状态i条件下，在m+n时刻转移到状态j的转移概率；当P{X m+n=j|Xm=i}只与i,j及n有关，且与m无关时，称转移概率具有平稳性，同时称此马氏链为齐次的或时齐的。time homogeneous..

n步转移概率《一步转移概率

homogeneous均匀的；齐次的，同种的

2、满足马氏性质的随机过程 2.1独立随机过程为马尔可夫过程 (1)n次投掷一枚硬币，第n次为止正面的次数； 2.2独立增量过程 （1）（二项分布）设在每次试验中，事件A发生的概率为p(0<p<1)，独立重复进行这项试验，以X（n）表示第n次为止A发生的概率，则{X（n），n=1,2,.....n} （2） 3 马氏过程的n维分布函数是由一些条件分布函数与初 始时刻对应的随机变量的分布函数的乘积得出 二、有限状态机 http://www.cnblogs.com/p2pstream/archive/2012/01/31/2333773.html

转载于:https://my.oschina.net/u/347414/blog/127827