掷骰子组合问题

2019独角兽企业重金招聘Python工程师标准>>>

掷N个骰子，最小值是Nx1，最大值是NxSides，组合数是Sides^N次方.

通过观察下面简单的2个骰子的情形，可以看出这是个典形的递归。

 

Index	Dice1	Dice2	Sum
1	1	1	2
2	1	2	3
3	1	3	4
4	1	4	5
5	1	5	6
6	1	6	7
7	2	1	3
8	2	2	4
9	2	3	5
10	2	4	6
11	2	5	7
12	2	6	8
13	3	1	4
14	3	2	5
15	3	3	6
16	3	4	7
17	3	5	8
18	3	6	9
19	4	1	5
20	4	2	6
21	4	3	7
22	4	4	8
23	4	5	9
24	4	6	10

 具体代码如下，可以分为从前往后处理，和分后往前处理两种情况

'Public Parameter
Public Out(), mOut, nOut     '输出数组
Public Nums%, Sides%         '骰子数，点数
Public Org()                 '多维数组
Public arr                   '临时变量

Sub Roll_Dice_2()
Dim i&, j&
Nums = 5             '骰子数量
Sides = 7            '骰子点数
ReDim Org(1 To Nums)
ReDim Out(1 To Sides ^ Nums, 1 To Nums)    '输出数组
ReDim arr(1 To Nums)          '临时数组
ReDim brr(1 To Sides)         '序列数组
For j = 1 To Sides
    brr(j) = j            '点数
Next j
For i = 1 To Nums
    Org(i) = brr     '将一维数组并入，产生多维数组
Next i
Dice_Combine_Recursion_Back 1, 1, Sides             '从后往前循环
Dice_Combine_Recursion_Front Nums, 1, Sides              '从前往后循环
Sheets("NxSides").Cells(2, 11).Resize(UBound(Out), UBound(Out, 2)) = Out
End Sub

'从后往前循环
'm表示骰子数
'k表示点数
Sub Dice_Combine_Recursion_Back(m, n, k)
Dim i, j                      '变量
For i = n To k               '循环点数
    arr(m) = Org(m)(i)       '数据写入
    If m < Nums Then
        Dice_Combine_Recursion_Back m + 1, n, k
    Else
        Arr_In_Out arr       '输出结果
    End If
Next i
End Sub

'从前往后循环
'm表示骰子数
'k表示点数
Sub Dice_Combine_Recursion_Front(m, n, k)
Dim i, j                     '变量
For i = n To k               '循环点数
    arr(m) = Org(m)(i)       '数据写入
    If m > 1 Then
        Dice_Combine_Recursion_Front m - 1, n, k
    Else
        Arr_In_Out arr       '输出结果
    End If
Next i
End Sub


'临时数组写入输出数组
Sub Arr_In_Out(arr)
nOut = nOut + 1
For mOut = 1 To UBound(arr)
    Out(nOut, mOut) = arr(mOut)
Next
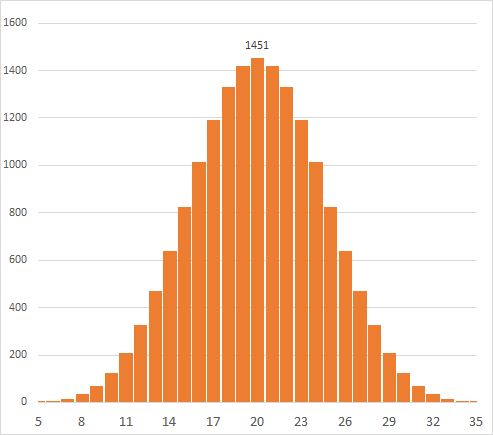
End Sub

下图是用递归计算的5个骰子，7个点面的分布情况。

具体文件可以从网盘下载

http://pan.baidu.com/s/1c10zH9u

 

转载于:https://my.oschina.net/tedzheng/blog/1549404