三角形的余弦定理

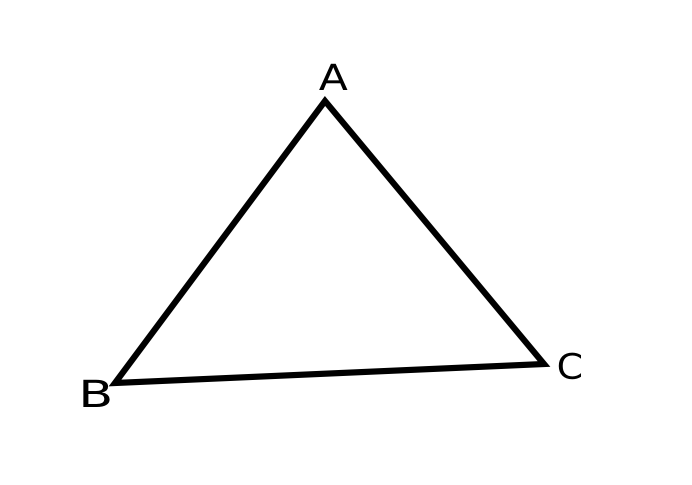
余弦定理:如图，三角形ABC,

则$$\cos B=\frac{|BA|^2+|BC|^2-|AC|^2}{2|BA||BC|}$$

证明余弦定理最初级的方法其实是用射影定理联立方程组.根据射影定理,我们知道

\begin{equation}\label{eq:1}|AB|\cos B+|AC|\cos C=|BC|\end{equation}

同理有

\begin{equation}\label{eq:2}|BC|\cos C+|AB|\cos A=|AC|\end{equation}

\begin{equation}\label{eq:3}|AC|\cos A+|BC|\cos B=|AB|\end{equation}

联立\ref{eq:1},\ref{eq:2},\ref{eq:3},我们发现了一个三元一次的线性方程组,未知数是$\cos A,\cos B,\cos C$,已知数是三条边的长度.将\ref{eq:1}$\times |BC|$-\ref{eq:2}$\times |AC|$可得:

\begin{equation}\label{eq:4}|BC|\cos B-|AC|\cos A=\frac{|BC|^2-|AC|^2}{|AB|}\end{equation}

再联立\ref{eq:3}和\ref{eq:4},容易解得$$\cos B=\frac{|BA|^2+|BC|^2-|AC|^2}{2|BA||BC|}$$

 

注1:勾股定理是余弦定理的特例,不妨设B是直角,则$\cos B=0$,因此此时$|BA|^2+|BC|^2=|AC|^2$.这就是勾股定理.

 

转载于:https://www.cnblogs.com/yeluqing/archive/2012/12/07/3827994.html