这两天一直在学习整数数组之类的问题,现在正好有机会和大家讨论一下.
C/C++中的int类型能表现的范围是-2E31-2E31–1。unsigned类型能表现的范围是0-2E32–1,即 0-4294967295。所以,int和unsigned类型变量,都不能保存超越10位的整数。有时我们须要介入运算的数,可能会远远不止10 位,例如,可能须要保存小数点前面100位(比如求π的值),那么,即便使用能表现很大数值范围的double变量,但是由于double变量只有64位,所以还是不可能到达准确到小数点前面100位这样的精度。
double变量的精度也不足以表现一个100位的整数。一般我们称这类基本数据类型无法表现的整数为大整数。如何表现和存放大整数呢?基本的思想就是:用数组存放和表现大整数。一个数组元素,存放大整数中的一位。
那么,如何解决类似大整数这样的高精度计算问题呢?
大数是指计算的数值非常大或者对运算的精度要求非常高,用已知的数据类型无法表现的数值。
计划思想如下:
1.用数组模拟大数的运算。
2.开一个比较大的整型数组,数组的元素代表数组的某一位或者某几位。
3.通过对数组元素的运算模拟大数的运算。
4.将数组输出。
大整数加法
问题:求两个不超越200位的非负整数的和
思绪:标题很明确告诉是很长的大整数相加,所以采取大数的加法;开一个整型数组,模拟加法:注意加法是尾对齐的。注意:1.不须要特别的数据结构;2.大数一般使用数组模拟。
首先要解决的就是存储200 位整数的问题。明显,任何C/C++固有类型的变量都无法保存它。最直观的想法是可以用一个字符串来保存它。字符串本质上就是一个字符数组,因此为了编程更方便,我们也可以用数组unsigned an[200]来保存一个200 位的整数,让an[0]存放个位数,an[1]存放十位数,an[2]存放百位数……
那么如何实现两个大整数相加呢?方法很简单,就是模拟小学生列竖式做加法,从个位开始逐位相加,超越或到达10 则进位。也就是说,用unsigned an1[201]保存第一个数,用unsigned an2[200]表现第二个数,然后逐位相加,相加的结果直接存放在an1 中。要注意处理进位。另外,an1 数组长度定为201,是因为两个200 位整数相加,结果可能会有201 位。
现实编程时,不一定要费心理去把数组大小定得正好合适,稍微开大点也无所谓,以免不小心没有算准这个“正好合适”的数值,而致使数组小了,发生越界错误。
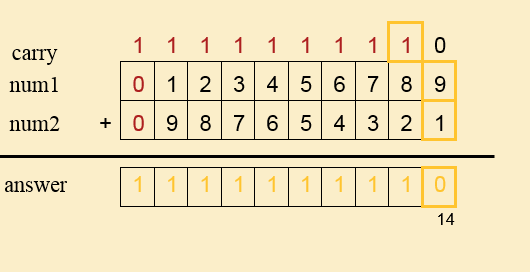
问 : 123456789 + 987654321 ?
答: 把 123456789存在num1当中,987654321存在num2,結果存在answer中
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
int an1[MAX_LEN+10];
int an2[MAX_LEN+10];
char szLine1[MAX_LEN+10];
char szLine2[MAX_LEN+10];
int main(void)
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
int nLen1 = strlen( szLine1);
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
for( i = 0;i < MAX_LEN ; i ++ )
{ an1[i] += an2[i]; //逐位相加
if( an1[i] >= 10 )
{ //看是不是要进位
an1[i] -= 10;
an1[i+1] ++; //进位
}
}
for( i = MAX_LEN; (i >= 0) && (an1[i] == 0); i -- ) ;
if(i>=0)
for( ; i >= 0; i--)
printf("%d", an1[i]);
else printf("0");
return 0;
}
大整数乘法
问题:求两个不超越200 位的非负整数的积。输入数据有两行,每行是一个不超越200 位的非负整数,没有多余的前导0。输出要求一行,即相乘后的结果。结果里不能有多余的前导0,即如果结果是342,那么就不能输出为0342。
先算835×9。5×9 失掉45 个1,3×9 失掉27 个10,8×9 失掉72 个100。由于不急于处理进位,所以835×9算完后,结果如下:
接下来算4×5。此处4×5 的结果代表20 个10,因此要 c[1]+=20,变成:

再下来算4×3。此处4×3 的结果代表12 个100,因此要 c[2]+= 12,变成:
最后算 4×8。此处4×8 的结果代表 32 个1000,因此要 c[3]+= 32,变成:

乘法进程完毕。接下来从 c[0]开始向高位逐位处理进位问题。c[0]留下5,把4 加到c[1]上,c[1]变成51
后,应留下1,把5 加到c[2]上……终究使得c 里的每个元素都是1 位数,结果就算出来了:
规律:一个数的第i位和另一个数的第j位相乘所得的数,一定是要累加到结果的第i+j位上。这里i,j都是从右往
左,从0开始数。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
int main(void)
{
int i, j;
int len1,len2;
int a[MAX_LEN+10],b[MAX_LEN+10],c[MAX_LEN*2+10];
char str1[MAX_LEN+10],str2[MAX_LEN+10];
for(i=0;i<MAX_LEN+10;i++) a[i]=b[i]=0;
for(i=0;i<MAX_LEN*2+10;i++) c[i]=0;
gets(str1); //按字符串形式读入第一个整数
gets(str2);
len1=strlen(str1);
for(j=0,i=len1-1; i>=0; i--)//把数字倒过来
a[j++]=str1[i]-'0';
len2=strlen(str2);
for(j=0,i=len2-1; i>=0; i--)//倒转第二个整数
b[j++]=str2[i]-'0';
for(i=0; i<len2; i++)//用第二个数乘以第一个数,每次一位
{
for(j=0; j<len1; j++)
c[i+j]+= b[i]*a[j]; //先乘起来,前面统一进位
}
for(i=0; i<MAX_LEN*2; i++)//循环统一处理进位问题
{
if(c[i]>=10)
{
c[i+1]+=c[i]/10;
c[i]%=10;
}
}
for(i=MAX_LEN*2; (c[i]==0)&&(i>=0); i--);//跳过高位的0
if(i>=0)
for(;i>=0;i--)
printf("%d", c[i]);
else
printf("0");
return 0;
}
大整数除法
基本的思想是重复做减法,看看从被除数里最多能减去多少个除数,商就是多少。一个一个减明显太慢,如何减得更快一些呢?以7546除以23 为例来看一下:开始商为0。先减去23 的100 倍,就是2300,发明够减3次,余下646。于是商的值就增长300。然后用646 减去230,发明够减2次,余下186,于是商的值增长20。最后用186 减去 23,够减8 次,因此终究商就是328。
所以本题的核心是要写一个大整数的减法函数,然后重复调用该函数进行减法操作。 计算除数的10倍、100倍的时候,不用做乘法,直接在除数前面补0 即可。
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
char szLine1[MAX_LEN + 10];
char szLine2[MAX_LEN + 10];
int an1[MAX_LEN + 10]; //被除数, an1[0]对应于个位
int an2[MAX_LEN + 10]; //除数, an2[0]对应于个位
int aResult[MAX_LEN + 10]; //存放商,aResult[0]对应于个位
//长度为 nLen1 的大整数p1 减去长度为nLen2 的大整数p2
//结果放在p1 里,返回值代表结果的长度
//如不够减返回-1,正好减完返回 0
int Substract( int * p1, int * p2, int nLen1, int nLen2)
{
int i;
if( nLen1 < nLen2 )
return -1;
//下面判断p1 是不是比p2 大,如果不是,返回-1
if( nLen1 == nLen2 )
{
for( i = nLen1-1; i >= 0; i -- )
{
if( p1[i] > p2[i] ) break; //p1>p2
else if( p1[i] < p2[i] ) return -1; //p1<p2
}
}
for( i = 0; i < nLen1; i ++ )
{ //要求调用本函数确保当i>=nLen2 时,p2[i] = 0
p1[i] -= p2[i];
if( p1[i] < 0 )
{
p1[i]+=10;
p1[i+1] --;
}
}
for( i = nLen1 -1 ; i >= 0 ; i-- )
if( p1[i] )//找到最高位第一个不为0
return i + 1;
return 0;//全体为0,说明两者相称
}
int main()
{
int t, n;
scanf("%d", &n);
for( t = 0; t < n; t ++ )
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
int nLen1 = strlen( szLine1);
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
memset( aResult, 0, sizeof(aResult));
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
if( nLen1 < nLen2 )
{
printf("0\n");
continue;
}
int nTimes = nLen1 - nLen2;
if(nTimes > 0)
{
for( i = nLen1 -1; i >= nTimes; i -- )
an2[i] = an2[i-nTimes];//朝高位挪动
for( ; i >= 0; i--)//低位补0
an2[i] = 0;
nLen2 = nLen1;
}
for( j = 0 ; j <= nTimes; j ++ )
{
int nTmp;
//一直减到不够减为止
//先减去若干个 an2×(10 的 nTimes 次方),
//不够减了,再减去若干个 an2×(10 的 nTimes-1 次方),......
while( (nTmp = Substract(an1, an2+j, nLen1, nLen2-j)) >= 0)
{
nLen1 = nTmp;
aResult[nTimes-j]++; //每胜利减一次,则将商的响应位加1
}
}
//下面输出结果,先跳过高位0
for( i = MAX_LEN ; (i >= 0) && (aResult[i] == 0); i -- );
if( i >= 0)
for( ; i>=0; i--)
printf("%d", aResult[i]);
else
printf("0");
printf("\n");
}
return 0;
}灯,带有一种明亮的光,每当深夜来临,是它陪伴着你,如此默默无闻。它是平凡的,外表华丽与否,那都是一样的,珍珠点缀,水晶加饰的灯它只能用以装饰,来满足人们的虚荣心,比起这,普普通通的日光灯是幸运的,因为它照明的本性没有改变,犹如生活中的一部份人平平凡凡却实实在在。
按照下面的思绪,我们可以把它统一起来做成一个大数包!我花了一个星期来实现这个大数包,不过测试数据很少,不太敢保障绝对正确,发出来仅供参考!
//下面的代码委曲算是bignum_beta1版本!
//实现了大整数的加减乘除四则运算,以及求两个整数的最大公约数,以及求乘法逆,miller_rabin生性检验,平方_乘法算法
//不足之处,位数还很难扩展至几千位,以及运算速度有一点慢,既然是beta1,说明bug还是挺多的
//程序缺乏测试数据来测试,所以有的结果不敢保障其正确性
//由于使用c++复写了很多运算符,加入这个文件之后,大数bignum可以看做是一个犹如犹如int一样的基本类型
//可以像int一样加减乘除和输入输出
#include<iostream>
#include<string>
#include<ctime>//用于发生随机数
using namespace std;
const int base=1000;//base用来表现数组中每个数的进制,逢base向前一位进1
const int MAX_LEN=300;//数组的最大长度
class bigNum{
public:
int num[MAX_LEN];
int len;
int flag;//增设一个标志,表现正负,这样大数包就能够扩展置负数
friend istream& operator>>(istream& input,bigNum &obj);
friend ostream& operator<<(ostream& output,bigNum& obj);
bigNum &operator=(const bigNum &s);//对于"="号的重载
//类的赋值运算符"="只能重载为成员函数,而不能把它重载为友元函数
bigNum();//构造函数
void eucli_setnum(int x);//设置数值
};
void bigNum::eucli_setnum(int x)//设置这个函数重要应对扩展的欧几里德算法
{
num[0]=x;
if(x!=0)
len=1;
else len=0;
}
bigNum::bigNum()//构造函数
{
memset(num,0,sizeof(num));//清零
len=0;
flag=1;//默许的数为正数
}
//关于下面的运算符重载函数,有一点须要特别记住,那就是len一定要记得更新,不然会出错!
//以下的几个函数都是逻辑运算符的重载函数
bool operator==(bigNum &a,bigNum &b)//"=="号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)
if(a.num[i]!=b.num[i])
return false;
return true;
}
bool operator!=(bigNum &a,bigNum &b)//"!="号的重载
{
for(int i=0;i<MAX_LEN;i++)
if(a.num[i]!=b.num[i])
return true;//只要有一个不相称,就返回true
return false;
}
/*
bool operator!=(bigNum &a,int &b)//"!="号的重载
{
if(a.num[0]!=b)
return false;//只要有一个不相称,就返回true
for(int i=1;i<MAX_LEN-1;i++)
if(a.num[i]!=0)
return false;
return true;
}*/
bool operator>(bigNum &a,bigNum &b)//">"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相称,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else return false;
return false;//两个数雷同也返回false
}
bool operator<(bigNum &a,bigNum &b)//"<"号的重载
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
{
if(a.num[i]!=b.num[i])//如果有两个数不相称,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
}
return false;
}
bool operator<=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相称,必定有一大一小
if(a.num[i]<b.num[i])
return true;
else
return false;
return true;//最后相称返回true
}
bool operator>=(bigNum &a,bigNum &b)
{
for(int i=MAX_LEN-1;i>=0;i--)//从最高位向下搜索
if(a.num[i]!=b.num[i])//如果有两个数不相称,必定有一大一小
if(a.num[i]>b.num[i])
return true;
else
return false;
return true;//最后相称返回true
}
bigNum &bigNum::operator=(const bigNum &s)//"="号的重载
{
if(this==&s) return *this;//防止s=s
for(int i=0;i<MAX_LEN;i++)
num[i]=s.num[i];
len=s.len;
flag=s.flag;
}
//以下几个函数是四则运算符的重载函数
bigNum operator-(bigNum a,bigNum b);//声明,防止编译出错
bigNum operator+(bigNum a,bigNum b)//加法的重载
{
bigNum sum;//存储结果
int i;
if(a.flag<0 && b.flag>0)//a为负,b为正,则a+b=b-|a|
{
a.flag=1;//这里对a进行了修改(将a变成正数),以便于进行减法运算,这也是重写不用引用的reason
sum=b-a;
if(b>a)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
if(a.flag>0 && b.flag<0)//a为正,b为负,则b+a=a-|b|
{
b.flag=1;
sum=a-b;
if(a>b)
sum.flag=1;//结果为正
else
sum.flag=-1;//结果为负
return sum;
}
//余下的情况是a,b两者符号雷同,即a+b=(|a|+|b|)*flag,flag与a,b符号分歧
for(i=0;i<MAX_LEN;i++)
{
sum.num[i]+=a.num[i]+b.num[i];
if(sum.num[i]>base)//超出base,则要进位
{
sum.num[i]-=base;
sum.num[i+1]++;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
sum.flag=a.flag;//如果a,b不是一正一负,那么a,b必定同号
return sum;
}
bigNum operator-(bigNum a,bigNum b)//减法的重载
{
bigNum sum;//存储结果
if(a.flag<0 && b.flag>0)//a为负,b为正,则a-b=-(|a|+|b|)
{
a.flag=1;
sum=b+a;
sum.flag=-1;//两个负数相加,结果一定为负数
return sum;
}
if(a.flag>0 && b.flag<0 && a>b)//a为正,b为负,则a-b=|a|+|b|
{
b.flag=1;
sum=b+a;
sum.flag=1;//两个正数相加,结果一定为正数
return sum;
}
//下面a,b的符号值分歧
if(a<b)//a<b,则|a|-|b|<0,转化为-(|b|-|a|)
{
sum=b-a;
sum.flag=-b.flag;
return sum;
}
//下面表现的就是|a|>|b|,且a,b同号
for(int i=0;i<MAX_LEN;i++)
{
a.num[i]-=b.num[i];
if(a.num[i]<0)//不够减时向前借位
{
a.num[i]+=base;
a.num[i+1]--;
}
if(a.num[i]!=0) a.len=i+1;//len要同步更新
}
return a;
}
bigNum operator*(bigNum &a,bigNum &b)//对于乘法的重载
{//乘法的flag已设置完毕
bigNum sum;
int i,j;
for(i=0;i<b.len;i++)//用第二个数b乘以第一个数a
{
for(j=0;j<a.len;j++)
sum.num[i+j]+=b.num[i]*a.num[j];//先乘起来,前面统一进位
}
for(i=0;i<MAX_LEN;i++)//循环统一处理进位问题
{
if(sum.num[i]>=base)
{
sum.num[i+1]+=sum.num[i]/base;
sum.num[i]%=base;
}
if(sum.num[i]!=0) sum.len=i+1;//len要同步更新
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;
else sum.flag=a.flag;
return sum;
}
int substract(int *p1,int *p2,int n1,int n2)
{
int i;
//被除数不能小于除数
if(n1<n2) return -1;//p2数的长度不能大于p1数的长度
if(n1==n2)//两数长度分歧情况下(所占用数组长度),p2数要小于p1数
{
for(i=n1-1;i>=0;i--)
{
if(p1[i]>p2[i]) break;
else if(p1[i]<p2[i]) return -1;
}
}
for(i=0;i<n1;i++)
{//减去一个p2值
p1[i]-=p2[i];
if(p1[i]<0)
{
p1[i]+=base;
p1[i+1]--;
}
}
for(i=n1-1;i>=0;i--)
if(p1[i])
return i+1;//返回所占用的数组长度
return 0;
}
bigNum operator/(bigNum a,bigNum b)//除法的重载
{//除法的flag设置完毕
bigNum sum;
int i,j;
if(a<b)//a<b时返回0
return sum;
int nTimes=a.len-b.len;
if(nTimes>0)
{
for(i=a.len-1;i>=nTimes;i--)
b.num[i]=b.num[i-nTimes];//朝高位挪动
for(;i>=0;i--)
b.num[i]=0;//低位补0
b.len=a.len;
}
for(j=0;j<=nTimes;j++)
{
int nTmp;
//一直减到不够减为止
while((nTmp=substract(a.num,b.num+j,a.len,b.len-j))>=0)
{
a.len=nTmp;
sum.num[nTimes-j]++;//每减胜利一次,则将商的对应为加1
}
if(sum.len==0 && sum.num[nTimes-j]!=0)
sum.len=nTimes-j+1;//同步更新len
}
//现在设置数的正负
if(a.flag+b.flag==0) sum.flag=-1;
else sum.flag=a.flag;
return sum;
}
bigNum operator%(bigNum &a,bigNum &b)//取模运算的重载
{
return a-b*(a/b);
}
istream& operator>>(istream& input,bigNum& obj)//重载输入函数
{//输入flag已设置完毕
string str;
input>>str;
int l=str.size();//l为字符串长度
int i,k,j;
for(j=0,i=base;i!=1;)
if(i>0)
{
j++;
i=i/10;
}//j用来表现base的位数
int p=l/j,q=l%j;//输入的数按照每个可以存放j个的标准,恰好放进,一共占用p个位置
if(q) obj.len=p+1;//当然,不一定恰好放进,就须要p+1个位置来放
else obj.len=p;
if(str[0]=='-')//输入为负数
obj.flag=-1;
else
obj.flag=1;//设置符号位,正数则flag为1,否则为-1
for(i=0;i<q;i++)//用来存放不能整除的高位部份
{
if(str[i]=='-') i++;//如果是负数的话,第一位不用处理
obj.num[p]=obj.num[p]*10+str[i]-'0';
}
p--;
for(;p>=0;p--)//下面的字符,以j为一组,字符个数恰好能够被j整除,一组组存入num数组里
{
for(k=1;k<=j;k++)
{
obj.num[p]=obj.num[p]*10+str[i]-'0';
i++;
}
}
return input;
}
ostream& operator<<(ostream& output,bigNum& obj)
{//输出flag就已设置好了
int i;
for(i=MAX_LEN-1; (i>=0)&&(obj.num[i]==0);i--);
if(i>=0)
{
if(obj.flag==-1) output<<'-';
for(;i>=0;i--)
output<<obj.num[i];
}
else
output<<'0';//整个数组都是0
return output;
}
bigNum extended_euclidean(bigNum n,bigNum m,bigNum &x,bigNum &y)//扩展的欧几里德算法的另一种形式
{
bigNum x1, x2, x3=n;
x1.eucli_setnum(1);
x2.eucli_setnum(0);
bigNum y1, y2, y3=m;
y1.eucli_setnum(0);
y2.eucli_setnum(1);
bigNum zero;
while(x3%y3!=zero)
{
bigNum d=x3/y3;
bigNum t1,t2,t3;
t1=x1-d*y1;
t2=x2-d*y2;
t3=x3-d*y3;
x1=y1; x2=y2; x3=y3;
y1=t1; y2=t2; y3=t3;
}
x=y1; y=y2;
return y3;
}
bigNum gcd(bigNum &n,bigNum &m)//求两个大数的最大公约数
{
bigNum x,y;
return extended_euclidean(n,m,x,y);
}
//求乘法逆其实也没有特别好的算法,重要还是依托欧几里德算法
bigNum mutirinverse(bigNum &n,bigNum &m)//求乘法逆
{
bigNum x,y;
extended_euclidean(m,n%m,x,y);
return x;
}
//平方——乘法算法
bigNum Square_and_Mutiply(bigNum a,bigNum m,bigNum n)
{
bigNum sum,zero,two;
two.eucli_setnum(2);
sum.eucli_setnum(1);
int length=1;
int bin[300];
//先将m转化为二进制
do
{
sum=m%two;
bin[length++]=sum.num[0];
m=m/two;
}while(m!=zero);
sum.eucli_setnum(1);
while(length>=0)
{
sum=(sum*sum)%n;
if(bin[length]==1)
{
sum=(sum*a)%n;
}
length--;
}
return sum;
}
//最后一个函数,用于素数判定的Miller-Rabin算法
bool wintess(bigNum a,bigNum n)
{
bigNum m,x,y,one,two,zero;
one.eucli_setnum(1);two.eucli_setnum(2);
bigNum i,j;
m=n-one;
while(m%two==zero)
{
m=m/two;
j=j+one;
}
x=Square_and_Mutiply(a,m,n);
for(i.eucli_setnum(1);i<=j;i=i+one)
{
y=Square_and_Mutiply(x,two,n);
if((y==one)&&(x!=one)&&(x!=n-one))
return true;
x=y;
}
if(y!=one) return true;
return false;
}
bool Miller_Robin(int times,bigNum &n)
//n为大于3的奇数,输出n是不是通过生性检验
{
bigNum a,one,two,random;
one.eucli_setnum(1);two.eucli_setnum(2);
if(n==one) return false; if(n==two) return true;
srand((unsigned)time(0));
for(int i=1;i<=times;i++)
{
random.eucli_setnum(rand());
a=random%(n-two)+two;
if(wintess(a,n)) return false;
}
return false;
}
int main()
{
bigNum a,b;
while(1)
{
cin>>a;
cin>>b;
cout<<a*b<<endl;
}
system("pause");
return 0;
}文章结束给大家分享下程序员的一些笑话语录: 爱情观
爱情就是死循环,一旦执行就陷进去了。
爱上一个人,就是内存泄露--你永远释放不了。
真正爱上一个人的时候,那就是常量限定,永远不会改变。
女朋友就是私有变量,只有我这个类才能调用。
情人就是指针用的时候一定要注意,要不然就带来巨大的灾难。
--------------------------------- 原创文章 By
整数和数组
---------------------------------


























 1711
1711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








