算法基础

2019独角兽企业重金招聘Python工程师标准>>>

一、基本概念

问题：需要回答的一般性提问，通常含若干参数。

算法：有限条指令的集合，确定某个问题的运算或操作的序列。

最坏情况时间复杂度：求解规模为n的实例所需最长时间w(n)。

平均情况时间复杂度：求解规模为n的实例所需要平均时间w(n)。

二、数学基础

1函数渐近的界

定义1.1设f和g是定义域为自然数N上的函数。

（1）若存在正整数c和n0，使得对一切n≥‍n0有0≤f(n)≤cg(n)‍成立，则称f(n)的渐近

 

的上界是g(n)，记作f(n)=O(g(n))。

 

（2）若存在正整数c和n0，使得对一切n≥n0有0≤cg(n)≤f(n)成立，则称f(n)的渐近

 

的上界是g(n)，记作f(n)=Ω(g(n))。

 

（3）若对于任意的正整数c都存在n0，使得当‍n≥n0有0≤f(n)<cg(n)‍成立，则记f(n)=o(g(n))。

 

（4）若对于任意的正整数c都存在n0，使得当n≥n0有0≤cg(n)<f(n)成立，则记f(n)=ω(g(n))。

 

（5）若f(n)=O(g(n))且‍f(n)=Ω(g(n))，则记作f(n)=Θ(g(n))‍

定理1.1设f和g是定义域为自然数的集合

定理1.2设f,g,h是定义域为自然数集合的函数

（1）如果f=O(g)且g=O(h)，那么f=O(h)

（2）‍如果f=Ω(g)且g=Ω(h)，那么f=Ω(h)‍

（3）如果f=Θ‍(g)且g=Θ(h)，那么f=Θ(h)‍

定理1.2 证（3）是（1）（2）的直接结果，（2）证明与（1）类似，仅证（1）

根据定义存在某个常数c1和n1，对所有的n≥n1，有f(n)≤c1g(n)。类似的，存在某个常数c2和n2，对所有的n≥n2，有g(n)≤c2h(n)。令n0=max{n1，n2}，当n≥n0时有f(n)≤c1g(n)≤c1c2h(n)，因此f=O(h)

定理1.3  假设‍f和g‍是定义域为自然数集合的函数，若对某个其它函数h，有f=O(h)和g=O(h)，‍那么f+g=O(h)‍

推论  假设‍f和g‍是定义域为自然数集合的函数，且满足g=O(f)，那么f+g=Θ(f)

定理1.3 与1.2类似

定理1.3推论 显然f+g=Ω(f)，因为对于所有的n≥0，有f(n)+g(n)≥f(n)。反之，由g=O(f)以及f=O(f)，由定理1.3知f+g=O(f)

定理1.4对每个b>1和α>0有logbn=o(nα)

定理1.5对每个r>1和每个d>0，有nd=o(rn)

定理1.4 1.5 洛必达法则可证

阶乘函数f(n)=n!是增长很快的函数，根据斯特灵公式，阶乘函数

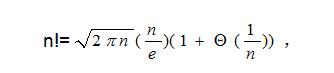
关于阶乘函数有下面结果：

n!=o(nn),n!=ω(2n)，log(n!)=Θ(nlogn)

前两个显而易见，仅提供第三个证明

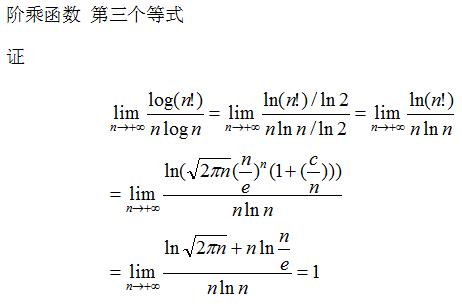
2求和方法

常见数列求和方法：

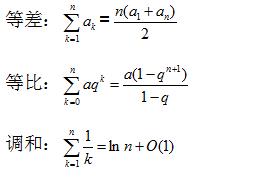
3递归方程求解

迭代归纳法：从原始方程开始，反复将左边函数用左边等式代入，得到初值，化简结果，再代入原方程验证。

递归树：初始递归树只有一个结点，权标记为W(n)，不断迭代，直至不含权为函数的结点为止。

例 4 用迭代递归法求解方程W(n)=2(n/2)+n-1,n=2k,W(1)=0

解 W(n)=2W(2k-1)+2k

=2[2W(2k-2)+2k-1-1]+2k-1

=...=2kW(1)+k2k-(2k-1+2k-2+..+2+1)

=k2k-2k+1

=nlogn-n+1

W(1)=1Xlog1-1+1=0符合初始条件，将结果代入原初始方程右边得

2W(n/2)+n-1=2[2k-1log2k-1+1]+2k-1

=2k(k-1)-2k+2+2k-1

=k2k-2k+1

=nlogn-n+1=W(n)

例5用递归树求递推方程T(n)=T(n/3)+T(2n/3)+n

定理1.6主定理 设a≥1，b>1为常数，f(n)为函数，T(n)为非负整数，且T(n)=aT(n/b)+f(n)

则有：

例 6 求递推方程T(n)=9T(n/3)+n

解 a=9,b=3,f(n)=n,那么

nlog39=n2,f(n)=O(nlog39-1),相当于主定理（1），故T(n)=Θ(n2)

例 7 求递推方程T(n)=T(2n/3)+1

解 a=1,b=3/2,f(n)=1,那么

nlog3/21=n0=1,f(n)=1，相当于主定理（2），故T(n)=Θ(logn)

例 8 求递推方程T(n)=3T(n/4)+nlogn

解 a=3,b=4,f(n)=nlogn,那么

nlogn=Ω(nlog43+ε)=Ω(n0.793+ε),ε≈0.2

要使af(n/b)<cf(n)成立，代入f(n)=nlogn，得到

3n/4log(n/4)≤cnlogn

显然只要c≥3/4，上式对充分大n成立，相当于主定理（3），故

T(n)=Θ(f(n)=Θ(nlogn)

例 9 插入算法和二分归并排序算法的时间复杂度

 

设W(n)表示顺序插入算法 InsertSort对于规模为n的输入在最坏情况下所做的比较次数。如果n-1个数已经排好，最坏的情况下需要将它与前n-1个数中的每一个进行1次比较，因此得到递推方程

                        W(n)=W(n-1)+n-1

                                          W(1)=0

由上面的求解知W(n)=n(n-1)/2=O(n2)

为了简单起见，不妨设n=2k,k为自然数。设W(n)表示二分归并排序算法在最坏情况下所做的比较次数，那么对n个数进行二分归并排序，W(n)满足如下递归方程：

W(n)=2W(n/2)+n-1

W(1)=0

由上面的求解知W(n)=O(nlogn) 

转载于:https://my.oschina.net/u/129126/blog/232751