XNA中三维空间物体的几种旋转方法

1. 通过绕三个坐标轴的旋转之和。

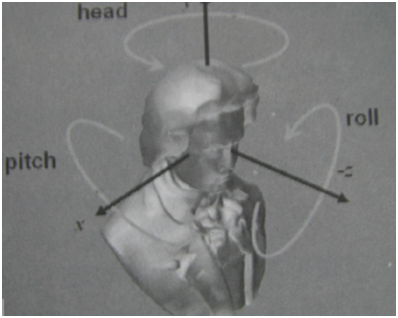
X、Y、Z分别描述绕三个坐标轴的旋转角度（0~360）。这三个角度称为欧拉角。绕X轴旋转的角称为倾斜角（pitch），绕Y轴旋转的角称为翻滚角（head或yaw），绕Z轴旋转的角称为摇摆角（roll）。物体的朝向一般可以用欧拉角表示，因此朝向的插值问题可以简单地转化为三个欧拉角的插值问题。但欧拉角表示也有它的局限性。因为旋转矩阵是不可交换的，基于欧拉角的旋转一定要按某个特定的次序进行；此外。等量的欧拉角变化不一定引起等量的旋转变化，从而导致旋转的不均匀；欧拉角还有可能导致自由度的丧失，出现万向节死锁现象。在使用三个旋转值来分别进行旋转变换的组合时，由于各个旋转是顺序进行的，绕一个轴的旋转会覆盖绕别的轴的旋转，会导致推动旋转的某个角度。例如：如果一个平行X轴的向量绕一个Y轴旋转90度，平等于X轴，那么，所有绕Z轴的旋转都不再起作用。

 

XNA中主要通过Matrix. CreateRotationX、Matrix. CreateRotationY、Matrix. CreateRotationZ方法实现欧拉角的旋转。这三个方法都是通过旋转角度生成一个旋转矩阵。如生成绕Y轴的旋转的矩阵代码如下：

 1 public   static  Matrix CreateRotationX( float  radians)
 2 {
 3    Matrix matrix;
 4    float num2 = (float) Math.Cos((double) radians);
 5    float num = (float) Math.Sin((double) radians);
 6    matrix.M11 = 1f;
 7    matrix.M12 = 0f;
 8    matrix.M13 = 0f;
 9    matrix.M14 = 0f;
10    matrix.M21 = 0f;
11    matrix.M22 = num2;
12    matrix.M23 = num;
13    matrix.M24 = 0f;
14    matrix.M31 = 0f;
15    matrix.M32 = -num;
16    matrix.M33 = num2;
17    matrix.M34 = 0f;
18    matrix.M41 = 0f;
19    matrix.M42 = 0f;
20    matrix.M43 = 0f;
21    matrix.M44 = 1f;
22    return matrix;
23}
24
25  
26
27  
28

XNA中也有一个Matrix.CreateFromYawPitchRoll方法，起初我也以为它是生成欧拉角旋转矩阵的，但在分析过他的实现代码后才发现，它其实是生成了一个四元数：

Code
1public static Matrix CreateFromYawPitchRoll(float yaw, float pitch, float roll)
2{
3    Matrix matrix;
4    Quaternion quaternion;
5    Quaternion.CreateFromYawPitchRoll(yaw, pitch, roll, out quaternion);
6    CreateFromQuaternion(ref quaternion, out matrix);
7    return matrix;
8}

这里是传说中将欧拉角转换为四元数的方法：

 1 public   static   void  CreateFromYawPitchRoll( float  yaw,  float  pitch,  float  roll,  out  Quaternion result)
 2 {
 3    float num9 = roll * 0.5f;
 4    float num6 = (float) Math.Sin((double) num9);
 5    float num5 = (float) Math.Cos((double) num9);
 6    float num8 = pitch * 0.5f;
 7    float num4 = (float) Math.Sin((double) num8);
 8    float num3 = (float) Math.Cos((double) num8);
 9    float num7 = yaw * 0.5f;
10    float num2 = (float) Math.Sin((double) num7);
11    float num = (float) Math.Cos((double) num7);
12    result.X = ((num * num4) * num5) + ((num2 * num3) * num6);
13    result.Y = ((num2 * num3) * num5) - ((num * num4) * num6);
14    result.Z = ((num * num3) * num6) - ((num2 * num4) * num5);
15    result.W = ((num * num3) * num5) + ((num2 * num4) * num6);
16}
17
18  
19
20  
21

2.绕任意轴旋转

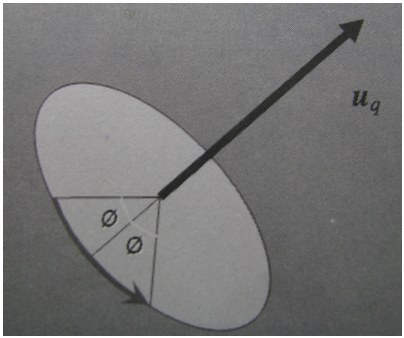
绕任意轴旋转需要两个参数：一个向量和一个角度，其中向量表示旋转轴，角度表示将要旋转的角度（0~360度）。

使用这种方法来进行旋转变化时，两个方向之间的插值不够够平滑，容易导致出现抖动等问题，如下图所示：

 

这种方法在XNA中主要通过 Matrix.CreateFromYawPitchRoll方法来实现。方法内容如下：

Code
 1public static Quaternion CreateFromAxisAngle(Vector3 axis, float angle)
 2{
 3    Quaternion quaternion;
 4    float num2 = angle * 0.5f;
 5    float num = (float) Math.Sin((double) num2);
 6    float num3 = (float) Math.Cos((double) num2);
 7    quaternion.X = axis.X * num;
 8    quaternion.Y = axis.Y * num;
 9    quaternion.Z = axis.Z * num;
10    quaternion.W = num3;
11    return quaternion;
12}

3.四元数旋转。

我们知道在实现绕任意轴旋转方面，以上两种方法都不够完美，而使用四元数来旋转则显得非常得体。

XNA中通过Matrix.CreateFromQuaternion方法创建旋转矩阵。实现方法如下：

 

Code
 1public static Matrix CreateFromQuaternion(Quaternion quaternion)
 2{
 3    Matrix matrix;
 4    float num9 = quaternion.X * quaternion.X;
 5    float num8 = quaternion.Y * quaternion.Y;
 6    float num7 = quaternion.Z * quaternion.Z;
 7    float num6 = quaternion.X * quaternion.Y;
 8    float num5 = quaternion.Z * quaternion.W;
 9    float num4 = quaternion.Z * quaternion.X;
10    float num3 = quaternion.Y * quaternion.W;
11    float num2 = quaternion.Y * quaternion.Z;
12    float num = quaternion.X * quaternion.W;
13    matrix.M11 = 1f - (2f * (num8 + num7));
14    matrix.M12 = 2f * (num6 + num5);
15    matrix.M13 = 2f * (num4 - num3);
16    matrix.M14 = 0f;
17    matrix.M21 = 2f * (num6 - num5);
18    matrix.M22 = 1f - (2f * (num7 + num9));
19    matrix.M23 = 2f * (num2 + num);
20    matrix.M24 = 0f;
21    matrix.M31 = 2f * (num4 + num3);
22    matrix.M32 = 2f * (num2 - num);
23    matrix.M33 = 1f - (2f * (num8 + num9));
24    matrix.M34 = 0f;
25    matrix.M41 = 0f;
26    matrix.M42 = 0f;
27    matrix.M43 = 0f;
28    matrix.M44 = 1f;
29    return matrix;
30}
31
32 
33
34 
35

 

Quaternion类的构造为Quaternion(float x, float y, float z, float w)，当然也还可以通过CreateFromAxisAngle、CreateFromRotationMatrix、CreateFromYawPitchRoll等方法将其它的旋转方法转换为四元数。  

 

转载于:https://www.cnblogs.com/desmend/archive/2008/09/20/1294880.html