动态规划---->每对定点之间的最短路径 Floyd（弗洛伊德）算法

最短路径

1、问题描述

设G = ( V, E)是一个有n 个结点的有向图。又设C 是G 的成本邻接矩阵, 其中C(i,i)= 0 , 1≤i≤n; 当〈i,j〉∈E (G)时, C( i,j) 表示边〈i,j〉的长度(或成本) ; 当i≠j 且〈i,j〉| E(G)时, C( i ,j) = ∞。每对结点之间的最短路径问题( all pair s shor test path problem) 是求满足下述条件的矩阵A: A 中的任何元素A(i,j) 是代表结点i到结点j的最短路径的长度

2、所有顶点间的最短路径—--用Floyd（弗洛伊德）算法

问题的提出：已知一个各边权值均大于0的带权有向图，对每一对顶点 v_i¹v_j，希望求出v_i与v_j之间的最短路径和最短路径长度。

解决思路：可以通过调用n次Dijkstra算法来完成，但时间复杂度为O(n³)。

改进： 弗洛伊德(Floyd)算法

算法思想：逐个顶点试探法

求最短路径步骤

1、初始时设置一个n阶方阵，令其对角线元素为0，若存在弧<V_i,V_j>，则对应元素为权值；否则为µ

2、逐步试着在原直接路径中增加中间顶点，若加入中间点后路径变短，则修改之；否则，维持原值

3、所有顶点试探完毕，算法结束

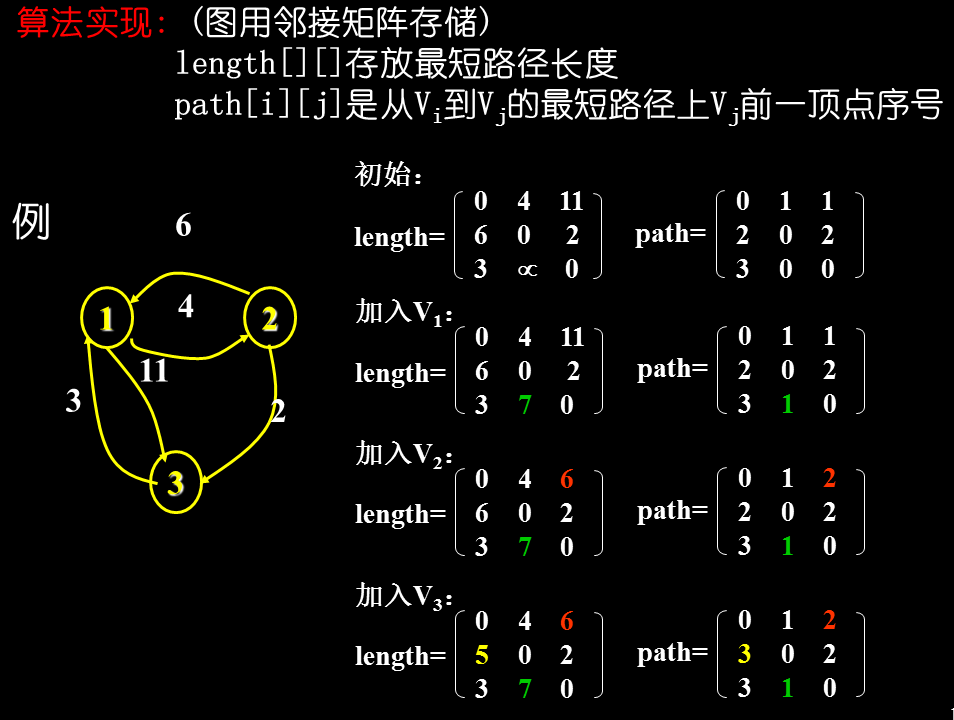
例子

 

Floyd 算法的程序的简单描述：       int  i, j,k;  // 标识结点       for (i=0; i<n; i++)            for (j=0; j<n; j++) A[i,j] = C[i,j];       for (i=0; i<n; i++ ) A[i,i] = 0;       for (k=0; k<n; k++)             for (i=0; i<n; i++)                 for (j=0; j<n; j++)           if (A[i,k]+A[k,j]<A[i,j])               A[i,j]=A[i,k]+A[k,j];