动态规划与分治方法相似,都是通过组合子问题的解来求解原问题.动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题.在这种情况下,分治算法会做许多不必要的工作,它会反复的求解那些公共子子问题.而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题都要重新计算,避免了这种不必要的计算工作.
动态规划方法通常用来求解最优化问题.这类问题可以有很多可行解,每个解都有一个值,我们希望寻找具有最优值的解.
15.1 钢条切割
钢条切割问题:给定一段长度为n英寸的钢条和一个价格表Pi( i=1, 2, ..., n ),求切割钢条方案,使得销售收益最大.
例如:
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格Pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
我们对每段的钢条进行最大收益值的计算:比如长度为9的钢条实际上最大收益值是25,分割成3 + 6=>8 + 17=25.而长度为10的钢条最大收益值不变,为30.Ri代表最大收益值
| Ri = 1 | 切割方案1 = 1 |
| Ri = 5 | 切割方案2 = 2 |
| Ri = 8 | 切割方案3 = 3 |
| Ri = 10 | 切割方案4 = 2 + 2 |
| Ri = 13 | 切割方案5 = 2 + 3 |
| Ri = 17 | 切割方案6 = 6 |
| Ri = 18 | 切割方案7 = 1 + 6 或 7 = 2 + 2+ 3 |
| Ri = 22 | 切割方案8 = 2 + 6 |
| Ri = 25 | 切割方案9 = 3 + 6 |
| Ri = 30 | 切割方案10 = 10 |
思想:为了求解规模为n的原问题,我们先求解形式完全一样,但规模更小的子问题.即当完成首次切割后,我们将两段钢条看成两个独立的钢条切割问题实例.我们通过组合两个相关子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大值,构成原问题的最优解.我们称钢条切割满足"最优子结构"性质:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解.
我们先来看一种解法相似(但效率很低)但更为简单的递归求解方法:我们将钢条从左边切割下长度为i的一段,只对右边剩下的长度为n-i的一段继续进行切割.
代码如下:
#include <stdio.h>
#include <stdlib.h>
int cut_rod( int arr[], int len )
{
int q = -1;
int i = 0;
int temp = 0;
if ( 0 == len ){
return 0;
}
for ( i = 0; i < len; i++ ){
q = q > ( temp = arr[ i ] + cut_rod( arr, len - i - 1 ) ) ? q : temp;
}
return q;
}
int main( void )
{
int arr[ 4 ] = { 1, 5, 8, 9 };
int result = 0;
result = cut_rod( arr, 4 );
printf("%d\n", result );
return 0;
} 
这段代码的难点在于此行代码的理解:
q = q > ( temp = arr[ i ] + cut_rod( arr, len - i - 1 ) ) ? q : temp;后面转念一下,为什么我们不能认为:arr[ 0 ]实际上切割的是钢条的右边( 类似数组的最右边的值 ),然后继续从左边进行递归( 毕竟切割钢条从右边开始和从左边开始是一样的 ),于是我理解了这个算法.
但是这个算法非常的低效,我这里进行了一个测试,代码如下:
PS:我很下贱的把数组扩充为arr[ 40 ],结果运行时间为2的40次方,很久很久,于是改为28.
#include <stdio.h>
#include <stdlib.h>
#include <Windows.h>
#include <time.h>
#define SIZE 28
int cut_rod( int arr[], int len )
{
int q = -1;
int i = 0;
int temp = 0;
if ( 0 == len ){
return 0;
}
for ( i = 0; i < len; i++ ){
q = q > ( temp = arr[ i ] + cut_rod( arr, len - i - 1 ) ) ? q : temp;
}
return q;
}
int main( void )
{
int arr[ SIZE ];
int result = 0;
clock_t start, finish;
int i = 0;
for ( i = 0; i < SIZE; i++ ){
arr[ i ] = i + 2;
}
start = clock();
result = cut_rod( arr, SIZE );
finish = clock();
printf("%d\n", result );
printf("using time %d 毫秒\n", finish - start );
return 0;
} 
如果说用的时间是2的28次方,那么长度改为27的话,应该花的时间为6.4秒那里,于是做了一次测试,把长度改为27:

确实,时间复杂度为指数级别.....这可是相当的恐怖,所以刚开始的时候,用了40的长度,自己算了一下,要用的时间是:6.4s x ( 2 ^ 13 ) = 52428.8s 约等于14.4个小时....( 幸好没等下去.... )
这种算法的主要问题在于:它重复的计算了相同的子问题,用动态规划方法可以解决这个问题.
动态规划方法的思想如下所述:动态规划方法仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来.如果随后再次需要此子问题的解,只需查找保存的结果,而不必重新计算.
动态规划有两种等价的实现方法:
第一种方法称为"带备忘的自顶向下法":此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解.当需要一个子问题的解时,过程首先检查是否已经保存过此解.如果是,则直接返回保存的值,从而节省了计算时间;否则,按通常方式计算这个子问题.
第二种方法称为自底向上法:这种方法一般需要恰当定义子问题"规模"的概念,使得任何子问题的求解都只依赖于"更小的"子问题的求解,因而我们可以将子问题按规模排序,按由小到大的顺序进行求解.当求解某个子问题时,它所依赖的那些更小的子问题都已求解完毕,结果已经保存.每个子问题只需求解一次,当我们求解它时,它的所有前提子问题都已求解完成.
我们来看看第一种自顶向下的代码和测试时间:
#include <stdio.h>
#include <stdlib.h>
#include <Windows.h>
#include <time.h>
#define SIZE 28
int memoized_cur_rod_aux( int arr[], int len, int r[] )
{
int result = 0;
int i = 0;
int temp = 0;
if ( r[ len ] >= 0 ){
return r[ len ];
}
if ( 0 == len ){
result = 0;
}
else{
result = -1;
for ( i = 0; i < len; i++ ){
result = result > ( temp = arr[ i ] + memoized_cur_rod_aux( arr, len - i - 1, r ) ) ? result : temp;
}
}
r[ len ] = result;
return result;
}
int main( void )
{
int arr[ SIZE ];
int result = 0;
clock_t start, finish;
int i = 0;
int temp[ SIZE + 1 ];
//这里临时数组的长度要比原数组大1,因为它需要判断len为0时候,temp会存储-1的索引值
//(当然,代码中不会出现-1,所以temp的索引从0~SIZE + 1 )
memset( temp, -1, sizeof( int ) * ( SIZE + 1 ) );
for ( i = 0; i < SIZE; i++ ){
arr[ i ] = i + 2;
}
start = clock();
result = memoized_cur_rod_aux( arr, SIZE, temp );
finish = clock();
printf("%d\n", result );
printf("using time %d 毫秒\n", finish - start );
return 0;
} 
我们把长度设为40看看:
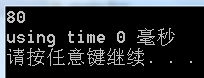
原来需要14.4个小时的运行时间,现在居然只用了0毫秒....我这次被震惊了....
我们来看看自底向上的方法:
自底向上的版本更简单,类似于冒泡法:先排列最小子问题,然后不断的向大问题靠拢,最后的大问题的解就是最优解:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
int bottom_up_cut_rod( int arr[], int len, int r[] )
{
int i = 0;
int j = 0;
int result = -1;
for ( j = 1; j <= len; j++ ){
//这里是<=len,是因为数组r的长度为len + 1.
//特别注意的是:数组索引从0开始导致实现的算法与伪代码的索引实际上很多地方都不一样
result = -1;
for ( i = 0; i <= j; i++ ){
result = result > ( arr[ i ] + r[ j - i - 1 ] ) ? result : arr[ i ] + r[ j - i - 1 ];
}
r[ j ] = result;
}
return r[ len ];
}
int main( void )
{
int arr[ 9 ] = { 1, 5, 8, 9, 10, 17, 17, 20, 24 };
int temp[ 10 ];
int result;
memset( temp, 0, sizeof( int ) * 10 );
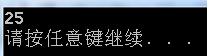
result = bottom_up_cut_rod( arr, 9, temp );
printf("%d\n", result );
return 0;
} 
虽然只要保证初始化时候,数组temp中temp[ 0 ]为0,但是最好还是全部初始化为0,防止意外的BUG.
当然,自顶向下方法和自底向上方法的运行时间复杂度都是O(n^2),比之前的指数运行时间好多了.
重构解:
我们之前的算法都是直接给出最优解,但是没有给出如何切割的方案,下列的代码就讲述如何切割:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
void bottom_up_cut_rod( int arr[], int len, int r[], int s[] )
{
int i = 0;
int j = 0;
int result = -1;
for ( j = 1; j <= len; j++ ){
//这里是<=len,是因为数组r的长度为len + 1.
//特别注意的是:数组索引从0开始导致实现的算法与伪代码的索引实际上很多地方都不一样
result = -1;
for ( i = 0; i <= j; i++ ){
if ( result < ( arr[ i ] + r[ j - i - 1 ] ) ){
result = arr[ i ] + r[ j - i - 1 ];
s[ j ] = i;
}
}
r[ j ] = result;
}
}
int main( void )
{
int arr[ 10 ] = { 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
int temp[ 11 ];
int index[ 11 ];
int i = 0;
memset( temp, 0, sizeof( int ) * 11 );
memset( index, 0, sizeof( int ) * 11 );
bottom_up_cut_rod( arr, 10, temp, index );
for ( i = 0; i < 11; i++ ){
printf("%3d ", index[ i ] );
}
printf("\n");
for ( i = 0; i < 11; i++ ){
printf("%3d ", temp[ i ] );
}
printf("\n");
return 0;
} 
我刚开始看的时候,不太理解输出,但是分析了以后才明白:比如25, 为索引9的最大收益值,它等于2, 1, 5, 1(向前数)这四个数字的和的组合,为3 + 6(当然你可以认为为什么不是2 + 7,2 + 7可以,但是它的长度为23,而不是25.)
当然,我们也可以看书上的算法,可能更明显的显示答案.
习题15.1-2:贪心策略
关于贪心策略,就是密度最大的意思:保证每一英寸的价值最大即可.我当时也是这种想,也想这样来计算最大收益值.但是为什么这种策略达不到最大收益值呢?
实际上分析也很简单:由于除法的基数值的线性递增(分母从1~10)并不代表除数值的线性递增,所以单位面积的最大收益值的相加实际上不代表整体最大收益值的相加.
15.2 矩阵链乘法






















 2649
2649

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








