topcoder srm 663 div1

problem1 link

每次枚举$S$的两种变化，并判断新的串是否是$T$的子串。不是的话停止搜索。

problem2 link

首先考慮增加１个面值为１的硬币后，$ways$数组有什么变化。设原来的方案为$w_{0}$，现在的为$w_{1}$。那么有$w_{1}[i]=w_{0}[i]+w_{0}[i-1]$。

$w_{0}: 1,5,6,7,0$

$w_{1}: 1,6,11,13,7$

如果将上面的例子中的$w_{0},w_{1}$看作多项式的话，就有$w_{0}=1+5x+6x^{2}+7x^{3}$,$w_{1}=1+6x+11x^{2}+13x^{3}+7x_{4}=(1+5x+6x^{2}+7x^{3})(1+x)=(1+x)w_{0}$

同理，面值为１的硬币增加$k$的话，就有$w_{1}[i]=\sum_{t=0}^{k}w_{0}[i-t]$，即多项式的话就是$w_{1}=(1+x)^{k}w_{0}$。如果是面值$v$的增加$k$的话，就是$w_{1}=(1+x^{v})^{k}w_{0}$。所以这里跟面值是１的是类似的。只分析面试为１的即可。

题目中是已知$w_{1}$来计算$w_{0}$，那么有$w_{0}=\frac{w_{1}}{(1+x)^{k}}$。

因为$ \frac{1}{1+x}=1-x+x^{2}-x^{3}+x^{4}...\rightarrow  \frac{1}{(1+x)^{k}}=(1-x+x^{2}-x^{3}+x^{4}...)^{k}=\sum_{n\geq 0}(-1)^{n}C_{k+n-1}^{n}x^{n}$

所以如果$w_{1}=\sum_{i=0}^{D}a_{i}x^{i},w_{0}=\sum_{i=0}^{D}b_{i}x^{i}$

那么$b_{D}=\sum_{i\geq 0}(-1)^{i}C_{k+i-1}^{i}a_{D-i}$

如果是面值为$v$的增加$k$个的话就有$b_{D}=\sum_{i\geq 0}(-1)^{i}C_{k+i-1}^{i}a_{D-iv}$.

这个代码是$O(qD)$的复杂度。不过一直超时，不知道怎么回事。

problem3 link

将卡片以及操作看作是图的顶点和边。每个节点有一个颜色$A$或者$B$。首先，节点０的颜色永远不会变。最后所有节点的颜色都会变成节点０的颜色。假设$[1,n-1]$中与节点０相同颜色的节点有$x$个。将这些节点称为$good$

一个结论是在任意次操作后（直到结束前），所有$x$个$good$节点的分布情况是等概率的。

所以可以计算一开始有$0,1,2,...,n-1$个$good$节点的期望。设$i$个点的时候的期望为$f(i)$。那么经过一次操作后，$i$个$good$点有可能变为$i-1,i,i+1$个$good$点，设概率为$p_{1},p_{2},p_{3}$

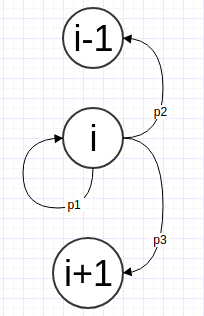
其中$p_{1}=\frac{C_{i+1}^{2}+C_{n-(i+1)}^{2}}{C_{n}^{2}}$,$p_{2}=\frac{i(n-(i+1))}{2C_{n}^{2}},p_{3}=1-p_{1}-p_{2}$

转移方程为$f(i)=p_{1}f(i)+p_{2}f(i-1)+p_{3}f(i+1)+t$,

$t=\left\{\begin{matrix} 0 & i \neq s\\  \frac{1}{C_{n-1}^{s}} & i=s \end{matrix}\right.$

$s$为输入中$good$ 节点的个数。

求出$f$数组后，答案为$\frac{\sum_{i=0}^{n-1}f(i)C_{n-1}^{i}}{2^{n}}$

 

code for problem1

#include <algorithm>
#include <string>
#include <unordered_set>
#include <vector>

class ABBADiv1 {
 public:
  std::string canObtain(const std::string &a, const std::string &b) {
    int n = static_cast<int>(b.size());
    sub_sets.resize(n + 1);
    for (int i = 0; i < n; ++i) {
      for (int j = i; j < n; ++j) {
        int len = j - i + 1;
        std::string s = b.substr(i, len);
        sub_sets[len].insert(s);
        std::reverse(s.begin(), s.end());
        sub_sets[len].insert(s);
      }
    }
    if (Dfs(a, b)) {
      return "Possible";
    }
    return "Impossible";
  }

 private:
  std::vector<std::unordered_set<std::string>> sub_sets;

  bool Exist(const std::string &s) { return sub_sets[s.size()].count(s) > 0; }

  bool Dfs(const std::string &a, const std::string &target) {
    if (a.size() == target.size()) {
      return a == target;
    }
    if (Exist(a + 'A') && Dfs(a + 'A', target)) {
      return true;
    }
    std::string new_a = a + 'B';
    std::reverse(new_a.begin(), new_a.end());
    return Exist(new_a) && Dfs(new_a, target);
  }
};

code for problem2

#include <algorithm>
#include <vector>

constexpr int kMAXN = 1002000;
long long p[kMAXN];
long long q[kMAXN];

class ChangingChange {
 public:
  std::vector<int> countWays(std::vector<int> ways,
                             std::vector<int> valueRemoved,
                             std::vector<int> numRemoved) {
    constexpr int kMod = 1000000007;
    int n = ways.size() - 1;
    int m = valueRemoved.size();
    auto ModInv = [&](long long k) {
      int t = kMod - 2;
      long long r = 1;
      while (t > 0) {
        if (t % 2 == 1) {
          r = r * k % kMod;
        }
        t /= 2;
        k = k * k % kMod;
      }
      return r;
    };
    p[0] = 1;
    for (int i = 1; i < kMAXN; ++i) {
      p[i] = i * p[i - 1] % kMod;
    }
    q[kMAXN - 1] = ModInv(p[kMAXN - 1]);
    for (int i = kMAXN - 2; i >= 0; --i) {
      q[i] = q[i + 1] * (i + 1) % kMod;
    }
    std::vector<int> result(m);
    for (int id = 0; id < m; ++id) {
      int k = valueRemoved[id];
      int num = numRemoved[id];
      long long total = 0;
      for (int i = 0, t = n / k; i <= t; ++i) {
        long long a = p[num + i - 1] * q[i] % kMod * q[num - 1] % kMod *
                      ways[n - i * k] % kMod;
        if ((i & 1) == 0) {
          total += a;
        } else {
          total += kMod - a;
        }
        if (total >= kMod) {
          total -= kMod;
        }
      }
      result[id] = static_cast<int>(total);
    }
    return result;
  }
};

code for problem3

#include <string>

constexpr int kMod = 1000000007;
constexpr int kMaxN = 1001;

int a[kMaxN][kMaxN];
int c[kMaxN][kMaxN];
int f[kMaxN];

class WarAndPeas {
 public:
  int expectedPeas(const std::string &state) {
    int n = static_cast<int>(state.size());
    c[0][0] = 1;
    for (int i = 1; i <= n; ++i) {
      c[i][0] = c[i][i] = 1;
      for (int j = 1; j < i; ++j) {
        c[i][j] = Add(c[i - 1][j - 1], c[i - 1][j]);
      }
    }
    int s = 0;
    for (int i = 1; i < n; ++i) {
      if (state[i] == state[0]) {
        ++s;
      }
    }
    for (int i = 0; i < n; ++i) {
      int p1 = Mul(Add(c[i + 1][2], c[n - i - 1][2]), Inverse(c[n][2]));
      int p2 = Mul(Mul(i, n - i - 1), Inverse(2 * c[n][2]));
      int p3 = Add(1, kMod - Add(p1, p2));
      if (i == n - 1) {
        p1 = 0;
      }
      p1 = Add(p1, kMod - 1);
      if (i == s) {
        a[i][n] = Mul(kMod - 1, Inverse(c[n - 1][s]));
      }
      a[i][i] = p1;
      if (i > 0) {
        a[i][i - 1] = p2;
      }
      if (i < n - 1) {
        a[i][i + 1] = p3;
      }
    }
    Solve(n);
    int result = 0;
    for (int i = 0; i < n; ++i) {
      result = Add(result, Mul(f[i], c[n - 1][i]));
    }
    result = Mul(result, Inverse(Pow(2, n)));
    return result;
  }

 private:
  void Solve(int n) {
    for (int i = 0; i < n; ++i) {
      for (int j = i; j < n; ++j) {
        if (a[j][i] != 0) {
          for (int k = 0; k <= n; ++k) {
            std::swap(a[i][k], a[j][k]);
          }
          break;
        }
      }
      for (int j = 0; j < n; ++j) {
        if (j == i || a[j][i] == 0) {
          continue;
        }
        int t = Mul(a[j][i], Inverse(a[i][i]));
        for (int k = 0; k <= n; ++k) {
          a[j][k] = Add(a[j][k], kMod - Mul(a[i][k], t));
        }
      }
    }
    for (int i = 0; i < n; ++i) {
      f[i] = Mul(a[i][n], Inverse(a[i][i]));
    }
  }

  int Pow(long long a, int b) {
    long long r = 1;
    while (b > 0) {
      if (b % 2 == 1) {
        r = r * a % kMod;
      }
      a = a * a % kMod;
      b /= 2;
    }
    return static_cast<int>(r);
  }

  int Inverse(int x) { return Pow(x, kMod - 2); }

  int Add(int x, int y) {
    x += y;
    if (x >= kMod) {
      x -= kMod;
    }
    return x;
  }

  int Mul(long long x, long long y) { return static_cast<int>(x * y % kMod); }
};

转载于:https://www.cnblogs.com/jianglangcaijin/p/6889705.html