抛物线习题

一、常用技巧

• 抛物线设点技巧，

如抛物线\(y^2=4x\)上任一点可以设为\((x，y)\)，但不如设为\((4t^2，4t)\)，运算简单。具体见例题13。

• 抛物线的焦点弦长公式\(|AB|=\cfrac{2p}{sin^2\alpha}\)的推导：

思路1：代数方法，联立方程组，

当直线的斜率不存在时，即直线的倾斜角\(\theta=90^{\circ}\)时，\(x_1=x_2=\cfrac{p}{2}\)，\(y_1=p\)，\(y_2=-p\)，

故\(|AB|=|y_1-y_2|=2p=\cfrac{2p}{sin^290^{\circ}}=\cfrac{2p}{sin^2\alpha}\)。

当直线的斜率存在时，即\(k=tan\theta\)，焦点弦方程是\(y=k(x-\cfrac{p}{2})\)，代入抛物线方程得到\(k^2x^2-(k^2p+2p)x+\cfrac{k^2p^2}{4}=0\)，

利用韦达定理可知\(x_1+x_2=\cfrac{k^2p+2p}{k^2}\)，由抛物线的定义

\(|AB|=|AF|+|BF|=x_1+x_2+p=\cfrac{k^2p+2p}{k^2}+p=\cfrac{2p(k^2+1)}{k^2}\)

\(=2p\times\cfrac{tan^2\theta+1}{tan^2\theta}=2p\times\cfrac{sin^2\theta+cos^2\theta}{sin^2\theta}=\cfrac{2p}{sin^2\theta}\)。

思路2：几何方法，利用三角函数。

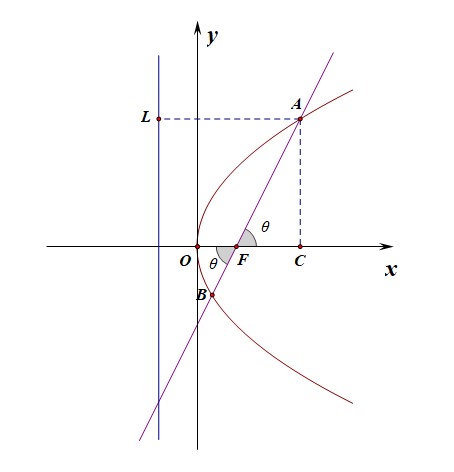
设\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，则由抛物线的定义可知，\(|AB|=x_1+x_2+p\)，

\(|AF|=x_1+\cfrac{p}{2}\)，\(|CF|=x_1-\cfrac{p}{2}\)，又\(|CF|=|AF|cos\theta\)，则可知

\(cos\theta(x_1+\cfrac{p}{2})=x_1-\cfrac{p}{2}\)，解得\(x_1=\cfrac{1+cos\theta}{1-cos\theta}\cdot \cfrac{p}{2}\)，同理求得\(x_2=\cfrac{1-cos\theta}{1+cos\theta}\cdot \cfrac{p}{2}\)，

将其代入\(|AB|=x_1+x_2+p\)，则\(|AB|=\cfrac{p}{2}(\cfrac{1-cos\theta}{1+cos\theta}+\cfrac{1+cos\theta}{1-cos\theta})+p\)，整理得到\(|AB|=\cfrac{2p}{sin^2\theta}\)。

记忆方法总结

• 焦点弦三角形的面积的最小值是\(AB\)为通经时；

如下图所示，抛物线\(y^2=2px\)，焦点\(F(1，0)\)，过点\(F\)的直线\(AB\)和抛物线交于点\(A\)，\(B\)，设点\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，则可知\(y_1y_2=-p^2\)；

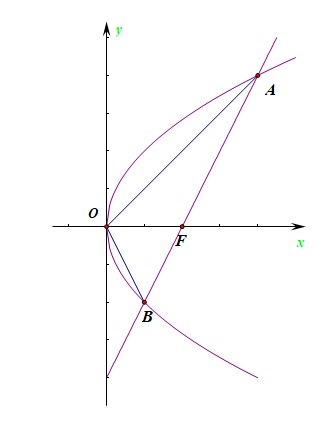
则\(S_{\triangle OAB}=\cfrac{1}{2}\times |OF|\times |y_1|+\cfrac{1}{2}\times |OF|\times |y_2|\)

\(=\cfrac{1}{2}\times |OF|\times (|y_1|+|y_2|)\ge \cfrac{1}{2}\times \cfrac{p}{2}\times 2\sqrt{|y_1y_2|}=\cfrac{p}{2}\cdot p=\cfrac{p^2}{2}\)；

当且仅当\(|y_1|=|y_2|\)时取到等号，即焦点弦三角形的面积的最小值是\(AB\)为通经时，其值为\(\cfrac{p^2}{2}\)。

给出方式

• 抛物线\(y^2=2px(p>0)\)经过点\((2，4)\)，即\(p=4\)$；

• 抛物线\(y^2=2px(p>0)\)的焦点到准线的距离为\(4\)，即\(p=4\)$；

二、抛物线性质

如下图所示，为抛物线\(y^2=2px\)的图像，过焦点\(F(\cfrac{p}{2}，0)\)的直线\(AB\)与抛物线相交于\(A(x_1，y_1)\)，且\(\angle xFA=\alpha\)，则有以下性质：

①\(x_1\cdot x_2=\cfrac{p^2}{4}\)；\(y_1\cdot y_2=-p^2\)；

②\(|AB|=x_1+x_2+p=\cfrac{2p}{sin^2\alpha}\)；

③\(S_{\triangle ABC}=\cfrac{p^2}{2sin\alpha}\)；

④\(\cfrac{1}{|AF|}+\cfrac{1}{|BF|}\)为定值；

⑤\(AB\)为焦点弦，当\(AB\perp x\)轴时，\(AB\)为通径；此时\(AB=2p\)；

三、典例剖析

例1已知点\(P(-3，2)\)在抛物线\(C：y^2=2px(p>0)\)的准线上，过点P的直线与抛物线C相切于A,B两点，则直线AB的斜率为多少？

分析：由题目先得到抛物线方程\(y^2=12x\)，对此式两边同时针对\(x\)求导，

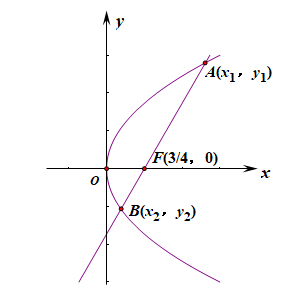
得到\(2y\cdot y'=12\)，即\(y'=\cfrac{6}{y}\)，

故经过抛物线上任意一点切线的斜率\(k=y'=\cfrac{6}{y}\)，

则以点\(A(x_1,y_1)\),\(B(x_2,y_2)\)为切点的切线方程分别为

\(y-y_1=\cfrac{6}{y_1}(x-x_1)\)；\(y-y_2=\cfrac{6}{y_2}(x-x_2)\)；

将点\(P(-3，2)\)坐标代入以上两个式子，

得到\(2-y_1=\cfrac{6}{y_1}(-2-x_1)\)；\(2-y_2=\cfrac{6}{y_2}(-3-x_2)\)；

又因为\(y_1^2=12x_1\)，\(y_2^2=12x_2\)，

解得\(y_1=3x_1-9\)；\(y_2=3x_2-9\)

即直线AB的方程为\(y=3x-9\)，故所求斜率为3.

课件地址

例2设抛物线\(C：y^2=3x\)的焦点，过F且倾斜角为\(30^{\circ}\)的直线交C于A，B两点，则\(|AB|\)等于（）

$A.\cfrac{\sqrt{30}}{3}$ $B.6$ $C.12$ $D.7\sqrt{3}$

【法1】：常规方法，利用两点间距离公式，由于\(2p=3\)，则\(\cfrac{p}{2}=\cfrac{3}{4}\)，故焦点\(F(\cfrac{3}{4}，0)\)，又斜率为\(k=\cfrac{\sqrt{3}}{3}\)，

则直线\(AB\)的方程为\(y=\cfrac{\sqrt{3}}{3}(x-\cfrac{3}{4})\)，

联立直线\(AB\)和抛物线方程，得到\(\left\{\begin{array}{l}{y^2=3x}\\{y=\cfrac{\sqrt{3}}{3}(x-\cfrac{3}{4})}\end{array}\right.\)，

消\(y\)得到\(16x^2-24\times7x+9=0\)，设点\(A(x_1，y_1)\)，点\(B(x_2，y_2)\)，

则\(x_1+x_2=\cfrac{24\times7}{16}=\cfrac{21}{2}\)，\(x_1x_2=\cfrac{9}{16}\)，

故\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|\)

\(=\sqrt{1+k^2}\cdot\sqrt{(x_1+x_2)^2-4x_1x_2}=12\)。

【法2】：利用直线\(AB\)的参数方程的参数的几何意义，

直线\(AB\)的参数方程为\(\begin{cases}x=\cfrac{3}{4}+\cfrac{\sqrt{3}}{2}t\\y=0+\cfrac{1}{2}t\end{cases}(t为参数)\)，将其代入\(y^2=3x\)中，

整理得到\(t^2-6\sqrt{3}t-9=0\)，设\(A\)，\(B\)对应的参数分别为\(t_1\)，\(t_2\)，

则\(\Delta>0\)，且有\(t_1+t_2=6\sqrt{3}\)，\(t_1t_2=-9\)，

故\(|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{36\times3-4\times(-9)}=12\)。

【法3】：利用抛物线的定义可知，\(|AB|=|AF|+|BF|=|AN|+|BO|=x_1+\cfrac{p}{2}+x_2+\cfrac{p}{2}=x_1+x_2+p\)，

故由法1中，得到\(x_1+x_2=\cfrac{24\times7}{16}=\cfrac{21}{2}\)，\(p=\cfrac{3}{2}\)，即\(|AB|=x_1+x_2+p=12\)。

法4：利用抛物线的焦点弦长公式：\(|AB|=\cfrac{2p}{sin^2\alpha}\)，

则\(|AB|=\cfrac{2\times \cfrac{3}{2}}{(\cfrac{1}{2})^2}=12\)。

例3【衡水金卷，直线过定点类型，较难】
如图所示，已知点\(A(-1，0)\)是抛物线的准线与\(x\)轴的交点，过点\(A\)的直线与抛物线交于点\(M，N\)两点，过点\(M\)的直线交抛物线于另一个点\(Q\)，且直线\(MQ\)过点\(B(1，-1)\).

(1).求抛物线的方程。

分析：由题目图形可知，\(\cfrac{p}{2}=1\)，则\(p=2\)，故顶点在坐标原点，开口向右的抛物线的方程为\(y^2=2px\)，即\(y^2=4x\)。

(2).求证：直线\(QN\)过定点。

分析：如果直线过定点\((m，n)\)，则直线的表达式必然应该能化为：\(y-n=k(x-m)\)类型。

设点\(M(4t^2，4t)\)，点\(N(4t_1^2，4t_1)\)，点\(M(4t_2^2，4t_2)\)，则由题目易知直线\(MN\)的斜率存在，

且\(k_{MN}=\cfrac{4t-4t_1}{4t^2-4t_1^2}=\cfrac{1}{t+t_1}\)，从而直线\(MN\)的方程是\(y=\cfrac{1}{t+t_1}(x-4t^2)+4t\)，即\(x-(t+t_1)y+4tt_1=0\)。

同理可知，直线\(MQ\)的方程\(x-(t+t_2)y+4tt_2=0\)，直线\(NQ\)的方程\(x-(t_1+t_2)y+4t_1t_2=0\)，

又点\(A\)在直线\(MN\)上，从而有\(4tt_1=1\)，即\(t=\cfrac{1}{4t_1}\)；点\(B\)在直线\(MQ\)上，

从而有\(1+(t+t_2)+4tt_2=0\)，即\(1+(\cfrac{1}{4t_1}+t_2)+4\times \cfrac{1}{4t_1}t_2=0\)，

化简得到\(4t_1t_2=-4(t_1+t_2)-1\)，

代入\(NQ\)的方程，得到\(x-(t_1+t_2)y-4(t_1+t_2)-1=0\)，

即\(y+4=\cfrac{1}{t_1+t_2}(x-1)\)，故直线\(NQ\)经过定点\((1，-4)\)。

• 抛物线\(y^2=4x\)上的任意点的坐标的设法一般是\((x，y)\)，本题采用\((4t^2，4t)\)，是抛物线的参数方程的一种。

• 注意直线过定点的证明思路。

例5【2019届宝鸡市高三理科数学质检Ⅰ第8题】平面直角坐标系\(xoy\)中，动点\(P\)与圆\((x-2)^2+y^2=1\)上的点的最短距离与其到直线\(x=-1\)的距离相等，则点\(P\)的轨迹方程为【】

$A.y^2=8x$ $B.x^2=8y$ $C.y^2=4x$ $D.x^2=4y$

分析：由题意可知，\(|PQ|=|PD|\)，但是用这个不好建立轨迹方程，或者不能有效的和抛物线的定义建立联系，

故等价转化为\(|PA|=|PB|\)，且其模型为\(y^2=2px\)。

这样就可以理解为平面内一个动点\(P\)到一个定点\(A\)的距离等于其到定直线\(x=-2\)的距离。

由抛物线的定义可知，\(-\cfrac{p}{2}=-2\)，即\(p=4\)，故\(y^2=2\times 4x=8x\)，故选\(A\)。

• 注意：抛物线的定义是高考考查时的高频考点。

例6已知抛物线\(y^2=2x\)的焦点为\(F\)，准线为\(l\)，且\(l\)与\(x\)轴交于点\(E\)，\(A\)是抛物线上的一点，作\(AB\perp l\)，垂直为\(B\)，\(|AF|=\cfrac{17}{2}\)，则四边形\(ABEF\)的面积等于【】

$A.19$ $B.38$ $C.18$ $D.36$

例7【2018高考新课标Ⅲ卷第16题】已知点\(M(-1，1)\)和抛物线\(C：y^2=4x\)，过\(C\)的焦点且斜率为\(k\)的直线与\(C\)交于\(A\)，\(B\)两点，若\(\angle AMB=90^{\circ}\)，则\(k\)=_________。

法1：点差法，做出如下示意图，连结\(MH\)，\(H\)为焦点弦\(AB\)的中点，

由于\(\triangle AMB\)为直角三角形，\(H\)为\(AB\)的中点，则\(MH=\cfrac{1}{2}AB\)，

又由于\(AB=AF+BF=AP+BQ\)，则\(MH=\cfrac{1}{2}AB=\cfrac{1}{2}(AP+BQ)\)，

故\(MH\)为直角梯形的中位线，则\(MH//x\)轴，

设\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，则有\(y_1^2=4x_1\) ①，\(y_2^2=4x_2\) ②，

①-②得到，\(y_1^2-y_2^2=4(x_1-x_2)\)，即\((y_1+y_2)(y_1-y_2)=4(x_1-x_2)\)，

则有\(\cfrac{y_1-y_2}{x_1-x_2}=\cfrac{4}{y_1+y_2}\)，即\(k=\cfrac{4}{y_1+y_2}\)，

又由于\(MH//x\)轴，\(M(-1，1)\)，则\(H\)点的纵坐标为1，即\(\cfrac{y_1+y_2}{2}=1\)，则\(y_1+y_2=2\)，代入上式，

得到\(k=\cfrac{4}{y_1+y_2}=2\).

法2：向量法，设直线\(AB：y=k(x-1)\)，由于点\(A，B\)都在抛物线上，故设\(A(4t_1^2，4t_1)\)，\(B(4t_2^2，4t_2)\)，

联立直线和抛物线，得到\(\left\{\begin{array}{l}{y=k(x-1)}\\{y^2=4x}\end{array}\right.\)，消\(x\)得到，

\(y^2-\cfrac{4}{k}y-4=0\)，则由韦达定理可知，\(4t_1+4t_2=\cfrac{4}{k}\)，\(4t_1\cdot 4t_2=-4\)，

即\(t_1+t_2=\cfrac{1}{k}\)，\(t_1\cdot t_2=-\cfrac{1}{4}\)，

又\(\overrightarrow{MA}=(4t_1^2+1，4t_1-1)\)，\(\overrightarrow{MB}=(4t_2^2+1，4t_2-1)\)，\(\angle AMB=90^{\circ}\)，

则\(\overrightarrow{MA}\cdot \overrightarrow{MB}=0\)，即\((4t_1^2+1)(4t_2^2+1)+(4t_1-1)(4t_2-1)=0\)，

打开整理得到，\(16(t_1t_2)^2+4(t_1^2+t_2^2)+1+16t_1t_2-4(t_1+t_2)+1=0\)，

代入整理得到，\(\cfrac{4}{k^2}-\cfrac{4}{k}+1=0\)，即\((\cfrac{2}{k}-1)^2=0\)，解得\(k=2\)。

例8已知抛物线\(C：y^2=4x\)的焦点为\(F\)，过点\(M(4，0)\)的直线与抛物线\(C\)交于\(A\)，\(B\)两点，则\(\triangle ABF\)的面积的最小值为【】

$A.8$ $B.12$ $C.16$ $D.24$

法1：做出如下的示意图，设直线\(AB\)的斜率为\(k\)，不妨只考虑\(k>0\)，则\(AB:y=k(x-4)\)，即\(kx-y-4k=0\)；

将直线和抛物线方程联立，消去\(x\)得到，\(ky^2-4y-16k=0\)，则\(y_1+y_2=-\cfrac{-4}{k}=\cfrac{4}{k}\)，\(y_1y_2=-16\)，

则\(|AB|=\sqrt{1+\cfrac{1}{k^2}}|y_1-y_2|=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}\)

\(=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(\cfrac{4}{k})^2-4\times (-16)}=\sqrt{\cfrac{k^2+1}{k^2}}\cdot 4\cdot \sqrt{\cfrac{4k^2+1}{k^2}}\)

\(=4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\)，

又点\(F\)到直线\(AB\)的距离为\(d=h=\cfrac{|3k|}{\sqrt{k^2+1}}=\cfrac{3k}{\sqrt{k^2+1}}\)，

则\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\cdot \cfrac{3k}{\sqrt{k^2+1}}\)

\(=6\times \cfrac{\sqrt{4k^2+1}}{k}=6\times \sqrt{4+\cfrac{1}{k^2}}\)，

当\(k\rightarrow \infty\)时，所求面积有最小值，\(S_{min}=6\times 2=12\)。故选\(B\).

法2：仿上利用均值不等式可以说明，当\(AB\)和\(x\)轴垂直时，\(S_{\triangle ABF}\)有最小值；

\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 3\cdot (|y_1|+|y_2|)\ge \cfrac{3}{2}\cdot 2\sqrt{|y_1y_2|}= \cfrac{3}{2}\cdot 2\cdot 4=12\)，故选\(B\).

例11【2019届高三理科数学二轮用题】已知抛物线\(C：y^2=ax(a>0)\)，若直线\(l：y=4x-a\)被抛物线\(C\)截得的弦长为\(17\)，则与抛物线\(C\)相切且平行于直线\(l\)的直线方程为【】

$A.4x-y+2=0$ $B.4x-y+1=0$ $C.8x-2y+1=0$ $D.8x-2y-1=0$

分析：如图所示，直线过抛物线的焦点，故利用抛物线的焦点弦长公式可得，\(\cfrac{2p}{sin^2\theta}=17\)，

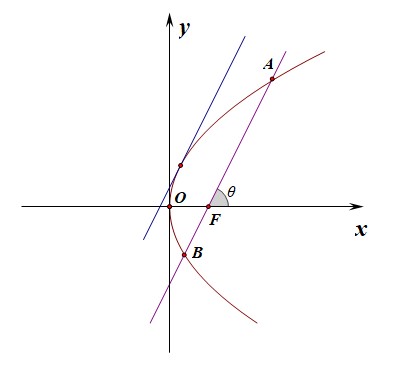
又由于直线的斜率\(k=4\)，则\(sin^2\theta=\cfrac{2p}{17}\)，\(cos^2\theta=\cfrac{17-2p}{17}\)，则\(k^2=16=tan^2\theta=\cfrac{2p}{17-2p}\)，

解得\(p=8\)，从而\(a=16\)，抛物线为\(y^2=16\)；

由图可知所求直线和抛物线相切于第一象限，故涉及到的函数为\(y=f(x)=4\sqrt{x}\)，

设切点为\(P(x_0，y_0)\)，则\(f'(x_0)=\cfrac{2}{\sqrt{x_0}}=4\)，求得\(x_0=\cfrac{1}{4}\)，\(y_0=2\)，

又所求直线的\(k=4\)，由点斜式方程可得，所求直线为\(4x-y+1=0\)，故选\(B\).

解后反思：焦点弦的公式不止一个，此处选用这一个就是考虑变量少，运算简单。

例12【2019届高三理科数学三轮用题】已知顶点在原点，焦点在\(x\)轴正半轴上的抛物线\(C\)，若其焦点到准线的距离为4，准线交\(x\)轴于点\(K\)，点\(A\)在抛物线\(C\)上，\(|AK|=\sqrt{2}|AF|\)，则\(\triangle AFK\)的面积为【】

$A.4$ $B.6$ $C.8$ $D.12$

分析：如图所示，由题可知，\(|OF|=|OK|=2\)，\(|KF|=4\)，由抛物线定义可知，\(|AF|=|AB|\)，则\(|AK|=\sqrt{2}|AB|\)，

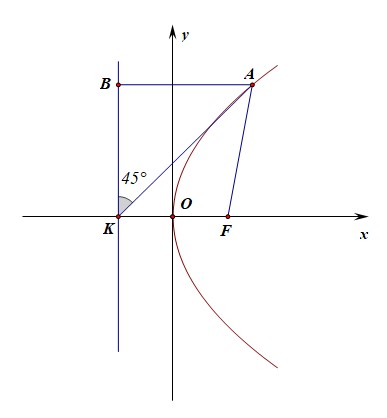
故可知\(\angle AKF=45^{\circ}\)，在\(\triangle AKF\)中，\(|KF|=4\)，设\(|AF|=x\)，则\(|AK|=\sqrt{2}x\)，

由余弦定理可知，\(|AF|=4\)，其高为\(|KB|=4\)，故\(S_{\triangle AFK}=\cfrac{1}{2}\times 4\times 4=8\)，故选\(C\)。

例13【2019届高三理科数学二轮用题】已知\(A\)，\(B\)为抛物线\(y^2=4x\)上的点，\(O\)为坐标原点，若\(\triangle OAB\)为等边三角形，则\(\triangle OAB\)的面积为【】

$A.24$ $B.48$ $C.24\sqrt{3}$ $D.48\sqrt{3}$

分析：如图所示，由于\(\triangle OAB\)为等边三角形，则边\(AB\)必然垂直于\(x\)轴，设点\(A(4t^2，4t)\)，则\(B(4t^2，-4t)\)，

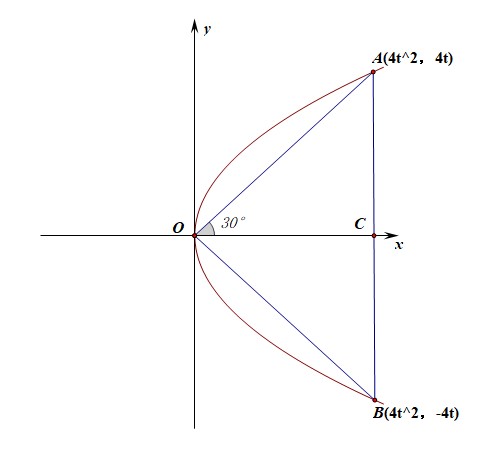
由于\(\angle AOC=30^{\circ}\)，则由斜率公式可知，\(\cfrac{4t}{4t^2}=tan30^{\circ}\)，解得\(t=\sqrt{3}\)，

故\(|AC|=|BC|=4\sqrt{3}\)，则\(|AB|=8\sqrt{3}\)，故高\(|OC|=4\sqrt{3}\times \sqrt{3}=12\)，

则\(S_{\triangle OAB}=\cfrac{1}{2}\times 8\sqrt{3}\times 12=48\sqrt{3}\)，故选\(D\).

例14【2019届高三理科数学二轮用题】

例15【2019届高三理科数学二轮用题】已知抛物线\(C：y^2=2px(p>0)\)的焦点到准线的距离为\(4\)，直线\(l'\)过点\((0，3)\)且和直线\(l：x-2y=0\)垂直，直线\(l'\)与抛物线\(C\)交于\(M\)，\(N\)两点，则以\(MN\)为直径的圆的方程为【】

$A.(x-\cfrac{5}{2})^2+(y+2)^2=20$ $B.(x+\cfrac{5}{2})^2+(y-2)^2=20$

$C.(x-\cfrac{5}{2})^2+(y+2)^2=10$ $D.(x+\cfrac{5}{2})^2+(y-2)^2=10$

分析：由题可知，抛物线方程为\(y^2=8x\)，直线\(l'\)方程为\(y-3=-2x\)，即\(l'：2x+y-3=0\)，

设点\(M(x_1，y_1)\)，\(N(x_2，y_2)\)，线段\(MN\)的中点为\((x_0，y_0)\)，联立\(y^2=8x\)和\(2x+y-3=0\)，

消去\(y\)得到\(4x^2-20x+9=0\)，由韦达定理得到\(x_1+x_2=5\)，\(x_1x_2=\cfrac{9}{4}\)，

则可知\(x_0=\cfrac{x_1+x_2}{2}=\cfrac{5}{2}\)，代入\(l'：2x+y-3=0\)，得到\(y_0=-2\)；即圆心坐标为\((\cfrac{5}{2}，-2)\)；

又由弦长公式得到\(MN=\sqrt{1+k^2}|x_1-x_2|\)

即\(MN=\sqrt{1+(-2)^2}\sqrt{(x_1+x_2)^2-4x_1x_2}=\sqrt{5}\sqrt{25-9}=4\sqrt{5}\)，

故半径为\(2\sqrt{5}\)，则以\(MN\)为直径的圆的方程为\((x-\cfrac{5}{2})^2+(y+2)^2=20\)，故选\(A\)。

转载于:https://www.cnblogs.com/wanghai0666/p/6920681.html