为什么正定矩阵等于转置_线性代数之——对称矩阵及正定性

当

是对称的时候，

有什么特殊的呢？

1. 对称矩阵的分解

如果

是对称矩阵，也就是

。对比以上两个式子，我们可以得到

，也就是

，

特征向量矩阵

是正交的

。

对称矩阵具有如下的性质：

• 它们的特征值都是实数；
• 可以选取出一组标准正交的特征向量。

每个对称矩阵都可以分解为

，

中为实数的特征值，

中为标准正交的特征向量。

• 例 1

特征值和特征向量分别为：

特征向量

位于零空间，特征向量

位于列空间。有子空间基本定理可知，零空间正交于行空间，这里

是对称矩阵，所以列空间和行空间是一样的，因此两个特征向量是垂直的。而要得到标准正交向量，我们只需再除以它们各自的长度即可。所以有：

一个实对称矩阵的所有特征值都是实数。

证明

实数的共轭还是它本身，两个数积的共轭等于共轭的积，即

。

对 (1) 进行转置可得

将

乘以

，将 (2) 式乘以

，可得

由于右边为向量长度的平方，因此不为零。对比 (3) 、(4) 两式可得

，所以对称矩阵的特征值一定为实数。

一个实对称矩阵的所有特征向量（对应于不同特征值）是正交的。

证明

假设有

和

，并且

，那么

等式左边为

，等式右边为

，因为

，所以有

，也即两个特征向量垂直。

• 例 2

特征向量分别为：

两个特征值的和为矩阵的迹，即对角线元素的和。

我们再来看

矩阵分解后的结果

扩展到

维的情况，

，其中每一个

都是投影矩阵，

，特征向量的长度为 1，所以分母略去了。也就是说，

对称矩阵是其特征向量投影矩阵的线性组合。

2. 实矩阵的复特征向量

针对对称矩阵，其特征值和特征向量都是实的。但是，非对称矩阵非常容易得到虚的特征值和特征向量。在这种情况下，

和

是不同的，我们得到了一个新的特征值

和新的特征向量

。

针对实矩阵，复数的特征值和特征向量总是一对共轭对。

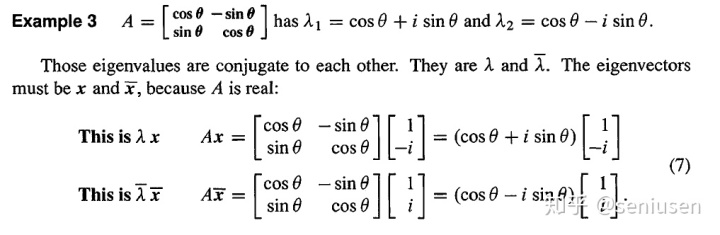
3. 特征值和主元

矩阵的主元和特征值是非常不同的，主元是通过消元得到的，而特征值是通过求解

得到的。到目前为止，它们唯一的联系就是：

所有主元的乘积等于所有特征值的乘积，都等于矩阵的行列式值。

针对对称矩阵，还有一个隐藏的关系：主元的符号和特征值的符号一致，也就是正的主元个数等于正的特征值的个数。

证明

对称矩阵可以被分解为

的形式。

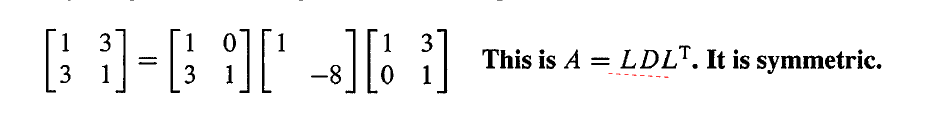
当

变成

的时候，

就变成了

，也就是由

变成了

。

的特征值为 4 和 -2，

的特征值为 1 和 -8。当

中左下角的元素从 3 变到 0 的时候，

就变成了

。在这个过程中，如果特征值符号发生改变的话，那肯定会有一个中间时刻，这时候特征值为 0，也就意味着矩阵是奇异的。但是最后的矩阵

一直有两个主元，始终是可逆的，从来不可能是奇异的，因此特征值的符号不会发生改变。

特别地，所有的特征值都大于零，也就是所有的主元都大于零，这种情况下，矩阵就称之为是正定的。

4. 重复的特征值

当没有重复特征值的时候，特征向量一定是线性不相关的，这时候矩阵一定可以被对角化。但是一个重复的特征值可能会导致特征向量的缺乏，这有些时候会发生在非对称矩阵上，但是对称矩阵一定会有足够的特征向量来进行对角化。

证明