C++实现数学表达式解析与计算项目实战

本文还有配套的精品资源，点击获取

简介：在C++编程中，数学表达式解析是一项重要且常见的任务，涉及中缀表达式到后缀表达式的转换及基于栈的求值。本项目实现一个支持括号和四则运算的简易计算器，采用逆波兰表达式（后缀表达式）转换算法（Shunting-yard算法）与栈结构完成表达式解析与计算。项目涵盖词法分析、优先级处理、负数与浮点数识别、错误检测等关键环节，适用于学习栈的应用、表达式求值原理及C++标准库（如std::stack、std::vector、std::istringstream）的实际使用。经过完整测试，该项目可作为数据结构与算法实践的经典案例。

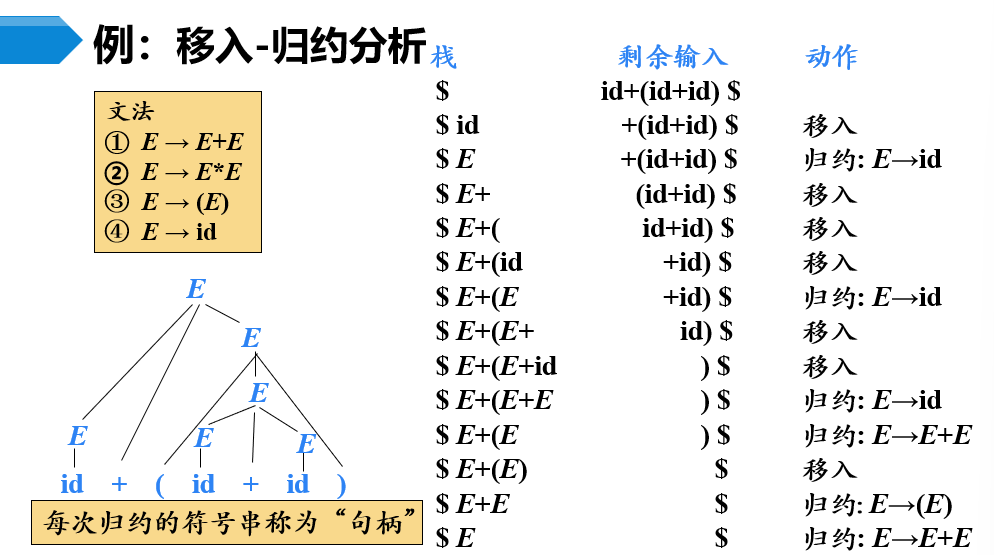
1. 数学表达式解析的基本概念与核心挑战

数学表达式解析是编译原理中的关键环节，旨在将人类书写的中缀表达式（如 3 + 4 * 2 ）转化为机器可高效计算的结构。其核心挑战在于协调运算符优先级、结合性与括号嵌套，例如 3 + 4 * 2 - 1 需先算乘法，体现 * 高于 + 的优先级。直接对中缀表达式求值易引发逻辑混乱，而转换为后缀形式（如逆波兰表示法）可消除括号、简化计算流程，为后续基于栈的求值提供基础。

2. 中缀到后缀表达式的转换机制

在程序语言处理系统中，数学表达式的求值往往不是直接对原始输入字符串进行操作，而是经历一系列结构化变换过程。其中最关键的一步便是将人类习惯书写的 中缀表达式 （Infix Expression）转换为计算机更易处理的 后缀表达式 （Postfix Expression），也称为逆波兰表示法（Reverse Polish Notation, RPN）。这一转换不仅是语法层面的重排，更是语义执行顺序的显式化过程。通过该机制，原本依赖括号和隐式优先级规则的复杂表达式被转化为无需上下文判断的操作序列，极大简化了后续求值逻辑。

本章深入剖析中缀到后缀表达式转换的核心原理与实现细节，重点围绕Dijkstra提出的Shunting-yard算法展开论述。从运算符位置差异带来的语义变化入手，逐步揭示栈结构如何协同输出队列完成符号调度；进一步探讨括号嵌套结构的合法性维护、浮点数识别中的状态建模，以及负号歧义消解等实际工程难题。整个分析过程结合形式化定义、流程图示、代码实现与参数解析，构建一个完整且可落地的技术闭环。

2.1 中缀与后缀表达式的语义差异

中缀表达式是人们日常书写算术公式的方式，其特点是 运算符位于两个操作数之间 ，例如 3 + 4 或 (5 * (6 + 2)) - 8 。这种写法符合自然语言直觉，但存在显著的解析难点：必须依据运算符优先级（如乘除高于加减）、结合性（左结合或右结合）以及括号控制流来确定计算顺序。而这些信息并未显式编码于表达式本身，导致解析器需要引入复杂的上下文推理机制。

相比之下，后缀表达式将运算符置于操作数之后，例如 3 4 + 表示先压入3和4，再执行加法。其最大优势在于 完全消除括号需求并固定操作顺序 ——只要按照从左到右扫描，遇到操作数就入栈，遇到运算符就弹出对应数量的操作数执行运算并将结果重新入栈，即可正确求值。这使得后缀表达式的求值过程具有确定性的状态机特征，非常适合自动化处理。

2.1.1 运算符位置对计算顺序的影响

运算符的位置决定了表达式结构的解析方式。以表达式 A + B * C 为例：

• 在中缀表示中，若无额外规则，默认按优先级解释为 A + (B * C) 。
• 若改为前缀（+ A * B C）或后缀（A B C * +），则顺序已由符号排列明确指定。

下表对比三种表示法在同一表达式下的形态：

表达式类型	示例： A + B * C
中缀	A + B * C
前缀	+ A * B C
后缀	A B C * +

观察可知，后缀表达式通过 延迟运算符应用 实现了优先级的自然体现： * 出现在 + 之前，意味着它会在栈中更早地作用于 B 和 C ，生成中间结果后再参与加法运算。因此，无需额外比较优先级即可保证正确的求值路径。

更重要的是，后缀表达式遵循严格的“操作数先行”原则，所有运算都基于栈顶元素进行。这意味着只要输入序列合法，求值过程就不会出现歧义。例如对于 2 3 + 4 * ，其执行步骤如下：

1. 推入 2
2. 推入 3
3. 遇到 + → 弹出 3 和 2，计算 2+3=5 ，推入 5
4. 推入 4
5. 遇到 * → 弹出 4 和 5，计算 5*4=20

最终栈中仅剩一个值 20 ，即为结果。

此过程可用以下 Mermaid 流程图描述：

graph TD
    A[开始] --> B{读取 Token}
    B -->|操作数| C[压入栈]
    B -->|运算符| D[弹出两个操作数]
    D --> E[执行运算]
    E --> F[将结果压入栈]
    C --> G[继续读取]
    F --> G
    G --> H{是否结束?}
    H -->|否| B
    H -->|是| I[返回栈顶值]

该流程图清晰展示了后缀表达式求值的状态转移逻辑：每个运算符触发一次二元操作，且仅当所有输入处理完毕后才输出最终结果。这种模式避免了递归下降解析中的回溯问题，提升了执行效率。

2.1.2 后缀表达式无括号特性及其计算优势

括号在中缀表达式中用于打破默认优先级规则，例如 (A + B) * C 显式要求先做加法。然而，在后缀表达式中，这类结构可通过调整符号顺序直接表达，如 A B + C * 。这里 + 出现在 * 之前，表明其作用域提前闭合，从而实现与括号相同的效果。

因此，后缀表达式本质上是一种“扁平化”的语法表示，其运算顺序完全由符号序列决定，不再依赖外部语法标记。这一特性带来了多个计算优势：

1. 求值逻辑简单统一 ：只需一个栈即可完成全部运算，无需构建抽象语法树（AST）或使用递归函数。
2. 易于硬件实现 ：早期计算器（如HP系列）广泛采用RPN设计，因其适合栈机架构。
3. 便于流水线处理 ：可在词法分析阶段边生成边求值，支持增量式计算。
4. 错误检测高效 ：非法序列（如缺少操作数）可在扫描过程中立即发现。

考虑如下复杂表达式：

((3 + 4) * 5) / 6

其对应的后缀形式为：

3 4 + 5 * 6 /

我们可以通过逐步模拟验证其正确性：

步骤	当前Token	栈内容（自底向上）	操作说明
1	3	[3]	压入操作数
2	4	[3, 4]	压入操作数
3	+	[7]	弹出4和3，计算3+4=7
4	5	[7, 5]	压入操作数
5	*	[35]	弹出5和7，计算7*5=35
6	6	[35, 6]	压入操作数
7	/	[5.833…]	弹出6和35，计算35/6≈5.833

可见，即使原表达式包含多层括号，转换后的后缀表达式仍能准确反映运算意图，且整个过程无需记忆任何优先级表或括号匹配状态。

此外，后缀表达式还具备良好的扩展性。例如支持一元运算符（如 -5 中的负号），只需修改求值器识别单目操作即可。类似地，函数调用（如 sin(0.5) ）也可映射为特殊运算符 sin ，并在遇到时弹出一个参数进行处理。

综上所述，后缀表达式以其结构简洁、语义明确、执行高效的特性，成为连接人类可读输入与机器可执行指令的理想桥梁。而实现这一转换的关键工具，正是下一节将详细介绍的Shunting-yard算法。

2.2 Dijkstra的Shunting-yard算法理论基础

由荷兰计算机科学家Edsger W. Dijkstra提出的Shunting-yard算法，是目前最经典且广泛应用的中缀转后缀方法。其名称来源于铁路调度场（shunting yard），形象比喻了操作符像车厢一样在轨道（栈）上暂存并有序释放的过程。该算法能够在线性时间内完成转换，并妥善处理运算符优先级、结合性及括号结构。

核心思想是使用两个数据结构： 一个用于暂存尚未输出的运算符的栈（operator stack） ，以及 一个用于收集最终后缀表达式的输出队列（output queue） 。算法逐个读取输入记号（token），根据其类型决定处理策略，最终将所有运算符按正确顺序输出至队列。

2.2.1 算法设计思想：操作符栈与输出队列的协同工作

Shunting-yard算法的工作流程可以概括为以下四类情况的分类处理：

1. 操作数 ：直接加入输出队列；
2. 左括号 ( ：压入操作符栈；
3. 右括号 ) ：不断弹出栈顶运算符至输出队列，直到遇到左括号；
4. 运算符（+、-、*、/ 等） ：比较当前运算符与栈顶运算符的优先级与结合性，决定是否弹出高位运算符。

该机制确保高优先级或先出现的运算符优先输出，低优先级的则保留在栈中等待。下面是一个典型的C++风格伪代码实现：

std::queue<Token> shuntingYard(const std::vector<Token>& tokens) {
    std::stack<Token> opStack;
    std::queue<Token> output;

    for (const auto& token : tokens) {
        switch (token.type) {
            case NUMBER:
                output.push(token);
                break;

            case LEFT_PAREN:
                opStack.push(token);
                break;

            case RIGHT_PAREN:
                while (!opStack.empty() && opStack.top().type != LEFT_PAREN) {
                    output.push(opStack.top());
                    opStack.pop();
                }
                if (!opStack.empty()) opStack.pop(); // 移除 '('
                break;

            case OPERATOR:
                while (!opStack.empty() && 
                       opStack.top().type == OPERATOR &&
                       hasHigherPrecedence(opStack.top(), token)) {
                    output.push(opStack.top());
                    opStack.pop();
                }
                opStack.push(token);
                break;
        }
    }

    while (!opStack.empty()) {
        output.push(opStack.top());
        opStack.pop();
    }

    return output;
}

代码逻辑逐行解读与参数说明：

• 第1行 ：函数接收一个Token向量作为输入，返回一个队列形式的后缀表达式。 Token 是自定义结构体，包含类型（number/operator/paren）和值。
• 第2–3行 ：声明操作符栈 opStack 和输出队列 output ，分别用于暂存运算符和构建结果。
• 第5–28行 ：遍历每个输入记号，按类型分发处理。
• 第7–9行 ：若为数字，直接送入输出队列，因为操作数总是最先出现在后缀表达式中。
• 第11–12行 ：左括号强制入栈，作为后续右括号匹配的基准点。
• 第14–19行 ：右括号触发循环出栈，直至找到匹配的左括号。期间所有中间运算符都被输出，体现了括号内子表达式的优先计算。
• 第21–27行 ：关键逻辑所在。对于新来的运算符，持续检查栈顶是否有更高优先级的运算符，若有则先行输出，以保证优先级高的先执行。
• 第29–33行 ：最后清空栈中剩余运算符（通常是低优先级的加减），完成转换。

该算法的时间复杂度为 O(n)，其中 n 为输入符号数量，每个符号最多入栈出栈一次。空间复杂度也为 O(n)，主要用于存储栈和队列。

为了更直观理解其运行机制，考虑表达式 3 + 4 * 5 的转换过程：

输入Token	动作	输出队列	操作符栈
3	输出	[3]	[]
+	入栈	[3]	[+]
4	输出	[3,4]	[+]
*	入栈（* > +）	[3,4]	[+, *]
5	输出	[3,4,5]	[+, *]
(结束)	出栈剩余	[3,4,5,*,+]	[]

最终输出 3 4 5 * + ，正确反映了 * 应先于 + 执行。

2.2.2 运算符优先级与右结合性的处理规则

标准算术运算符大多为 左结合 （left-associative），即相同优先级下从左向右计算，如 8 - 4 - 2 解释为 (8-4)-2 而非 8-(4-2) 。但在某些情况下存在 右结合 （right-associative）运算符，典型例子是幂运算 ^ ，通常规定 2^3^4 = 2^(3^4) 。

Shunting-yard算法需区分这两种结合性，否则会导致语义错误。处理规则如下：

• 对于 左结合 运算符：当新运算符与栈顶同优先级时，应弹出栈顶（先算左边）；
• 对于 右结合 运算符：即使优先级相等也不立即弹出，允许其留在栈中形成右深结构。

为此， hasHigherPrecedence 函数需增强为：

bool shouldPop(const Token& topOp, const Token& currentOp) {
    if (topOp.precedence > currentOp.precedence)
        return true;
    if (topOp.precedence < currentOp.precedence)
        return false;
    // 相等时看结合性：左结合则弹出，右结合则不弹
    return topOp.isLeftAssociative;
}

参数说明：

• topOp : 栈顶运算符，已有上下文；
• currentOp : 当前输入运算符；
• precedence : 整数优先级，越大越高；
• isLeftAssociative : 布尔值，指示结合方向。

例如处理 2 ^ 3 ^ 4 ：

输入	输出队列	栈	说明
2	[2]	[]	输出
^	[2]	[^]	入栈
3	[2,3]	[^]	输出
^	[2,3]	[^, ^]	优先级相同但右结合，不弹出
4	[2,3,4]	[^, ^]	输出
结束	[2,3,4,^,^]	[]	出栈两次

结果为 2 3 4 ^ ^ ，对应 2^(3^4) ，符合预期。

下表列出常见运算符的优先级与结合性配置建议：

运算符	优先级	结合性	说明
^	4	右	幂运算
* , /	3	左	乘除
+ , -	2	左	加减
( , )	-	-	特殊处理

该表格可用于初始化哈希表或常量数组，在解析时快速查询。

综上，Shunting-yard算法不仅解决了优先级问题，还能通过结合性标志精确控制运算顺序，是构建健壮表达式引擎的基础组件。

2.3 支持括号的结构化解析流程

括号是中缀表达式中改变运算优先级的重要手段，其合法性直接影响表达式的语法正确性。Shunting-yard算法通过栈机制天然支持括号处理，但仍需严谨设计边界条件与异常检测路径。

2.3.1 左括号入栈与右括号触发的出栈机制

左括号 ( 被视为“新的作用域起点”，一旦出现即入栈，不参与优先级比较。它的唯一配对对象是右括号 ) 。当遇到 ) 时，算法启动“括号封闭”流程：持续弹出栈顶运算符并输出，直到遇见 ( ，然后将其丢弃（不输出）。

这一机制保障了括号内部的所有运算符都能在外部运算之前被处理。例如表达式 3 * (4 + 5) 的转换过程如下：

输入	输出队列	操作符栈	操作说明
3	[3]	[]	输出
*	[3]	[*]	入栈
(	[3]	[*, (]	左括号入栈
4	[3,4]	[*, (]	输出
+	[3,4]	[*, (, +]	入栈
5	[3,4,5]	[*, (, +]	输出
)	[3,4,5,+]	[*]	弹出 + ，移除 (
结束	[3,4,5,+,*]	[]	弹出 *

结果为 3 4 5 + * ，等价于 3*(4+5) ，验证成功。

值得注意的是， 左括号不能参与常规优先级比较 。例如 + 不会因为优先级低于 * 就弹出 ( 之前的 * ，因为括号形成了隔离屏障。

2.3.2 多层括号嵌套的合法性判断路径

深层嵌套如 ((a + b) * c) + d 是常见场景。算法通过栈深度自动管理层次结构：每层 ( 开启新层级， ) 关闭当前层。合法性检测包括：

1. 右括号过多 ：若未找到匹配的 ( ，报错；
2. 左括号残留 ：结束后栈中仍有 ( ，说明未闭合；
3. 空括号 ：如 () ，虽语法合法但语义无效，可根据需求拒绝。

以下为增强版右括号处理逻辑：

case RIGHT_PAREN:
    bool found = false;
    while (!opStack.empty()) {
        Token top = opStack.top();
        if (top.type == LEFT_PAREN) {
            opStack.pop(); // 移除 '('
            found = true;
            break;
        } else {
            output.push(top);
            opStack.pop();
        }
    }
    if (!found) {
        throw std::runtime_error("Mismatched parentheses: unmatched ')'");
    }
    break;

异常处理说明：

• 使用布尔标志 found 记录是否成功匹配；
• 若循环结束仍未发现 ( ，抛出异常；
• 支持定位错误位置（可通过记录token索引实现）；

此外，可在主控流程结束后添加最终校验：

while (!opStack.empty()) {
    if (opStack.top().type == LEFT_PAREN) {
        throw std::runtime_error("Unclosed '(' detected");
    }
    output.push(opStack.top());
    opStack.pop();
}

这样便能全面覆盖括号错误类型。

2.4 浮点数与负号的词法区分策略

真实表达式常含小数和负数，如 -3.14 或 5 * (-2 + 1) 。此时面临两大挑战：

1. 如何正确识别浮点数字面量？
2. 如何区分减号 - 是二元操作符还是负号？

2.4.1 负数符号与减法操作符的上下文判定

关键在于 上下文分析 ：若 - 出现在表达式开头、左括号后或另一个运算符之后，则它是 一元负号 ；否则为 减法运算符 。

例如：

• -5 → 一元负号
• 3 - 5 → 减法
• (-5 + 3) → 括号内的负号

解决方案是在词法分析阶段引入“期待操作数”标志：

enum Context { EXPECT_OPERAND, EXPECT_OPERATOR };

Context ctx = EXPECT_OPERAND;

for (char c : expr) {
    if (c == '-' && ctx == EXPECT_OPERAND) {
        tokens.emplace_back(UNARY_MINUS);
    } else if (isdigit(c) || c == '.') {
        parseNumber(expr, pos); // 包含符号处理
        ctx = EXPECT_OPERATOR;
    } else if (isOperator(c)) {
        tokens.emplace_back(BINARY_OP, c);
        ctx = EXPECT_OPERAND;
    }
}

如此便可精准区分两种用途。

2.4.2 小数点在数字识别中的状态转移模型

识别浮点数需状态机支持。基本状态包括：

• START
• IN_INT（整数部分）
• AFTER_DOT（小数点后）
• IN_FRAC（小数部分）

转换图如下：

stateDiagram-v2
    [*] --> START
    START --> IN_INT: digit
    IN_INT --> IN_INT: digit
    IN_INT --> AFTER_DOT: '.'
    AFTER_DOT --> IN_FRAC: digit
    IN_FRAC --> IN_FRAC: digit
    IN_FRAC --> [*]
    IN_INT --> [*]

配合代码：

double parseNumber(const string& s, int& pos) {
    double integerPart = 0, fractionalPart = 0;
    int fracDigits = 0;
    bool isNegative = false;
    bool hasDot = false;

    if (s[pos] == '-') {
        isNegative = true;
        ++pos;
    }

    while (pos < s.length() && isdigit(s[pos])) {
        integerPart = integerPart * 10 + (s[pos++] - '0');
    }

    if (pos < s.length() && s[pos] == '.') {
        hasDot = true;
        ++pos;
        while (pos < s.length() && isdigit(s[pos])) {
            fractionalPart = fractionalPart * 10 + (s[pos++] - '0');
            fracDigits++;
        }
    }

    double result = integerPart + fractionalPart / pow(10, fracDigits);
    return isNegative ? -result : result;
}

该函数返回完整数值，并更新位置指针，供后续解析使用。

综上，通过对词法层面的精细建模，系统可稳健支持现代数学表达式的多样化输入需求。

3. 基于std::stack的表达式求值实践

在数学表达式解析系统中，后缀表达式（也称逆波兰表示法，RPN）因其无需括号、计算顺序明确等特性，成为实现高效求值的理想形式。一旦完成从中缀到后缀的转换，下一步便是对生成的后缀表达式进行实际数值求值。这一步骤的核心依赖于栈结构——特别是C++标准库提供的 std::stack 容器适配器。本章深入探讨如何利用 std::stack<double> 作为操作数栈，在运行时动态管理中间结果，并通过状态驱动机制精确执行每一步运算。

3.1 栈数据结构在表达式计算中的角色定位

3.1.1 std::stack容器适配器的接口特性与性能特征

std::stack 是C++ STL中的一种容器适配器，它封装了底层容器（默认为 std::deque ），仅暴露符合“后进先出”（LIFO）原则的操作接口。其主要成员函数包括：

• push(const T&) : 将元素压入栈顶
• pop() : 移除栈顶元素（不返回值）
• top() : 返回栈顶元素的引用
• empty() : 判断栈是否为空
• size() : 获取当前栈中元素个数

虽然 std::stack 本身不是一个独立容器，而是基于其他容器构建的适配层，但它提供了清晰且安全的抽象边界，非常适合用于表达式求值这类需要严格控制访问顺序的场景。

#include <stack>
#include <vector>
#include <iostream>

int main() {
    std::stack<double> operandStack;

    operandStack.push(3.14);
    operandStack.push(2.71);

    double b = operandStack.top(); operandStack.pop();
    double a = operandStack.top(); operandStack.pop();

    std::cout << "Popped values: " << a << ", " << b << "\n";
    return 0;
}

代码逻辑逐行分析：

1. #include <stack> 引入栈模板定义；
2. 声明一个存储 double 类型的栈 operandStack ；
3. 使用 push() 将两个浮点数依次压入栈中，此时栈内布局为 [3.14, 2.71] （底部到顶部）；
4. 调用 top() 获取栈顶值并赋给 b ，随后调用 pop() 移除该元素；
5. 再次取新栈顶赋给 a 并弹出；
6. 输出表明取出顺序为 2.71 , 3.14 ，验证了LIFO行为。

特性	描述
底层容器可配置	支持 vector , deque , list 作为基础容器
时间复杂度	所有操作均为 O(1)
空间开销	deque 默认分段连续分配，适合频繁增删
安全性保障	不支持随机访问，防止非法越界操作

使用 std::vector 作为底层容器可通过以下方式指定：

std::stack<double, std::vector<double>> fastStack;

这种方式在某些性能敏感场景下可能更优，因为 vector 具有更好的缓存局部性。

graph TD
    A[开始求值] --> B{输入token}
    B -->|操作数| C[压入operandStack]
    B -->|运算符| D[弹出两个操作数]
    D --> E[执行运算]
    E --> F[结果压回栈]
    F --> B
    B -->|结束| G[检查栈大小]
    G --> H{栈中仅剩一个元素?}
    H -->|是| I[输出结果]
    H -->|否| J[语法错误]

该流程图展示了整个后缀表达式求值过程的状态流转，其中 std::stack 处于中心位置，负责维护所有未完成计算的操作数。

3.1.2 LIFO原则与后缀表达式逐项求值的天然契合

后缀表达式的本质在于：每个运算符总是作用于其前面最近的若干操作数。这种“延迟绑定”的特性与栈的LIFO行为高度匹配。

例如，考虑表达式 3 4 + 5 * 的求值过程：

步骤	输入Token	栈状态（自底向上）	动作说明
1	3	[3]	压入操作数
2	4	[3, 4]	压入操作数
3	+	[7]	弹出4和3，计算3+4=7，压入结果
4	5	[7, 5]	压入操作数
5	*	[35]	弹出5和7，计算7*5=35，压入结果

最终栈中只剩一个元素 35 ，即为表达式结果。

这种模式之所以有效，是因为后缀表达式隐式编码了计算顺序。每当遇到一个二元运算符时，必然已有足够的前置操作数可供使用，而栈恰好能以正确顺序提供它们（最后入栈的操作数作为右操作数）。

对于非交换运算如减法和除法，顺序至关重要。以下代码演示了减法处理时的参数顺序问题：

if (token == "-") {
    if (operandStack.size() < 2) throw std::runtime_error("Insufficient operands");
    double b = operandStack.top(); operandStack.pop();
    double a = operandStack.top(); operandStack.pop();
    operandStack.push(a - b); // 注意：a 是左操作数，b 是右操作数
}

此处必须确保先弹出的是右操作数（后出现的），再弹出的是左操作数（先出现的）。若颠倒顺序，则会导致 3 4 - 被错误解释为 4 - 3 而非预期的 3 - 4 。

此外， std::stack 的轻量级封装并未牺牲性能。现代编译器对模板实例化优化良好，使得 push / pop 调用几乎等价于直接操作底层容器的末尾。结合CPU缓存预取机制，连续的栈操作表现出极佳的运行效率，特别适合在高频求值任务中部署。

3.2 后缀表达式求值算法实现步骤

3.2.1 扫描输入序列的状态机驱动逻辑

后缀表达式求值本质上是一个确定性有限自动机（DFA）的过程。输入符号流被逐个读取，根据其类型进入不同的处理分支。我们将这一过程建模为状态驱动的扫描器，其核心是一个循环配合条件判断。

假设输入是一组已切分好的Token（字符串向量），如下所示：

std::vector<std::string> rpnTokens = {"3.14", "2.71", "+", "5", "*", "2", "/"};

对应的求值主循环如下：

double evaluateRPN(const std::vector<std::string>& tokens) {
    std::stack<double> s;

    for (const auto& token : tokens) {
        if (isNumber(token)) {
            s.push(std::stod(token));
        }
        else if (isOperator(token)) {
            handleBinaryOperation(s, token);
        }
        else {
            throw std::invalid_argument("Invalid token: " + token);
        }
    }

    if (s.size() != 1) {
        throw std::logic_error("Malformed expression: stack has " + 
                              std::to_string(s.size()) + " elements at end");
    }

    return s.top();
}

参数说明：

• tokens : 经过词法分析后的后缀记号序列，每个元素为操作数或运算符字符串。
• 返回值：表达式最终结果，类型为 double 。
• 抛出异常：非法输入或结构错误时中断执行。

该函数遵循严格的单入口单出口原则，内部通过辅助函数解耦职责。其中 isNumber() 可采用尝试解析的方式实现：

bool isNumber(const std::string& str) {
    try {
        size_t pos;
        std::stod(str, &pos);
        return pos == str.length();
    } catch (...) {
        return false;
    }
}

这种方法能正确识别正负浮点数、科学计数法（如 1e-5 ）、整数等形式。

3.2.2 操作数压栈与二元运算弹栈的控制流设计

关键部分在于运算符处理函数的设计。下面是一个典型的 handleBinaryOperation 实现：

void handleBinaryOperation(std::stack<double>& s, const std::string& op) {
    if (s.size() < 2) {
        throw std::runtime_error("Not enough operands for operator '" + op + "'");
    }

    double b = s.top(); s.pop();
    double a = s.top(); s.pop();
    double result;

    if (op == "+") result = a + b;
    else if (op == "-") result = a - b;
    else if (op == "*") result = a * b;
    else if (op == "/") {
        if (std::abs(b) < 1e-9) {
            throw std::domain_error("Division by zero");
        }
        result = a / b;
    }
    else if (op == "^") {
        result = std::pow(a, b);
    }
    else {
        throw std::invalid_argument("Unsupported operator: " + op);
    }

    s.push(result);
}

逐行逻辑解读：

1. 首先检查栈中至少有两个操作数，否则表达式不完整；
2. 按照“先弹出右操作数，再弹出左操作数”的顺序取出 b 和 a ；
3. 使用 if-else 链匹配运算符并执行对应算术运算；
4. 对除法进行零值检测，避免运行时崩溃；
5. 计算完成后将结果重新压入栈中，供后续运算使用。

此设计体现了“操作即状态变更”的思想：每一个运算符都改变栈的状态，推动计算向前演进。

为了提升可扩展性，可以引入函数表来替代冗长的 if-else 判断：

using BinOpFunc = double(*)(double, double);

std::map<std::string, BinOpFunc> opMap = {
    {"+", [](double a, double b){ return a + b; }},
    {"-", [](double a, double b){ return a - b; }},
    {"*", [](double a, double b){ return a * b; }},
    {"/", [](double a, double b){
        if (std::abs(b) < 1e-9) throw std::domain_error("Div by zero");
        return a / b;
    }},
    {"^", std::pow}
};

// 在handleBinaryOperation中替换为：
result = opMap.at(op)(a, b);

这种方式不仅提高了代码整洁度，还便于后期添加自定义函数（如 % , max , min 等）。

3.3 特殊数值情况的处理方案

3.3.1 浮点数精度保留与科学计数法支持

在真实应用场景中，用户常输入高精度或极小/极大数值，如 6.022e23 （阿伏伽德罗常数）或 1.6e-19 （电子电荷）。 std::stod 原生支持这些格式，无需额外处理。

然而，输出时需注意精度控制。默认情况下， std::cout 可能以科学计数法或截断形式显示结果，影响用户体验。建议统一设置输出精度：

#include <iomanip>
std::cout << std::fixed << std::setprecision(6) << result << std::endl;

setprecision(6) 表示保留6位小数， fixed 强制使用定点表示法。

对于中间计算过程中的累积误差，应选用双精度浮点型（ double ），其IEEE 754标准提供约15-17位有效数字，足以满足大多数工程计算需求。

此外，在比较浮点数是否为零时，禁止使用 == ，而应采用相对误差判断：

bool isZero(double x) {
    return std::abs(x) < 1e-9;
}

阈值 1e-9 可根据应用领域调整。金融类系统可能要求更高精度（如 1e-12 ），而图形学计算则可适当放宽。

3.3.2 除零异常的预判与运行时捕获机制

尽管可以通过 try-catch 捕获除零异常，但C++浮点运算并不会抛出硬件异常（除非启用FPU异常）。因此必须显式检查除数是否接近零。

改进版除法处理如下：

else if (op == "/") {
    constexpr double EPSILON = 1e-9;
    if (std::abs(b) < EPSILON) {
        std::ostringstream msg;
        msg << "Division by near-zero value (" << b << ") detected";
        throw std::domain_error(msg.str());
    }
    result = a / b;
}

同时，在主调用端应具备异常传播能力：

try {
    double res = evaluateRPN(tokens);
    std::cout << "Result: " << res << std::endl;
} catch (const std::exception& e) {
    std::cerr << "Evaluation failed: " << e.what() << std::endl;
}

这种防御性编程策略显著增强了系统的鲁棒性，避免因单一错误导致程序崩溃。

3.4 错误传播与中间状态调试技术

3.4.1 栈空状态下非法弹栈的断言保护

在求值过程中，最常见的运行时错误是试图从空栈中弹出元素。这通常意味着表达式语法错误，如缺少操作数或运算符过多。

为此，每次 pop() 前必须进行断言检查：

double popTop(std::stack<double>& s) {
    if (s.empty()) {
        throw std::underflow_error("Attempt to pop from empty stack");
    }
    double val = s.top();
    s.pop();
    return val;
}

将其集成进运算处理逻辑：

double b = popTop(s);
double a = popTop(s);

这样既实现了错误隔离，又提升了代码复用性。

3.4.2 计算完成后栈内残留元素的语义检查

合法的后缀表达式求值结束后，栈中应 恰好 剩余一个元素——即最终结果。任何其他情况均表示表达式不完整或存在多余操作数。

if (s.size() > 1) {
    throw std::logic_error("Too many operands left in stack");
}
if (s.size() < 1) {
    throw std::logic_error("No result produced");
}

此类检查应在函数末尾强制执行，形成闭环验证。

为进一步辅助调试，可在开发阶段添加日志功能：

void printStack(const std::stack<double>& s) {
    std::stack<double> temp = s; // 复制副本以便遍历
    std::vector<double> elems;
    while (!temp.empty()) {
        elems.push_back(temp.top());
        temp.pop();
    }
    std::reverse(elems.begin(), elems.end());
    std::cout << "Stack: ";
    for (auto x : elems) std::cout << x << " ";
    std::cout << "\n";
}

该函数可用于输出每步操作后的栈状态，帮助定位错误发生点。

综上所述，基于 std::stack 的表达式求值不仅是理论可行的，而且借助C++标准库的强大支持，能够以简洁、高效、安全的方式实现工业级强度的计算引擎。

4. 词法分析器（Lexer）与优先级表的设计实现

在构建一个完整的数学表达式解析系统时，词法分析是整个流程的起点。它承担着将原始字符串输入分解为具有语义意义的“记号”（Token）序列的任务，是语法分析和后续求值操作的基础。若词法分析阶段出现误切分或类型识别错误，即使后续算法再严谨，最终结果也必然出错。因此，设计一个健壮、可扩展且高效的词法分析器（Lexer），并辅以清晰的运算符优先级管理机制，是实现高可靠性表达式解析的关键一步。

本章将深入探讨如何从一串看似简单的数学表达式字符流中提取出结构化的 Token 序列，重点剖析数字（包括整数、浮点数、负数）与符号（运算符、括号）的识别策略。同时，引入基于哈希表的优先级映射机制，使系统能够灵活支持多种运算符及其结合性规则。通过封装 Token 类型体系，并定义模块间的数据传递契约，确保 Lexer 输出能无缝对接 Shunting-yard 算法等后续处理模块，形成一条逻辑清晰、类型安全、异常可控的数据流水线。

4.1 表达式字符串的词法分解过程

词法分析的核心任务是从输入字符串中逐字符扫描，依据预设的文法规则将其切分为一个个具有独立语义的记号（Token）。这些 Token 包括操作数（如 3.14 、 -2.5 ）、运算符（如 + 、 * ）、括号（ ( 、 ) ）等基本元素。这一过程虽然看似简单，但在实际实现中需处理诸多边界情况，例如连续字符是否属于同一数字、负号与减号的上下文区分、小数点合法性判断等。

为了高效完成词法切分，通常采用状态机驱动的方式进行字符分类与累积。每当遇到数字字符（0-9 或 ‘.’），进入“数字收集模式”；当遇到运算符或括号，则立即生成对应的符号 Token；空白字符可被跳过以增强容错性。关键在于如何正确提取带符号的浮点数，尤其是形如 -3.14 这类表达式中的负数识别。

4.1.1 字符流到记号（Token）序列的切分逻辑

词法分析的本质是对输入字符串进行 词素划分 （Lexical Scanning），即将字符序列划分为最小语义单位。对于数学表达式 "3 + -2.5 * (7.1 - 1)" ，期望输出如下 Token 序列：

Token 类型	值
Number	3
Operator	+
Number	-2.5
Operator	*
LeftParen	(
Number	7.1
Operator	-
Number	1
RightParen	)

该过程需要解决两个核心问题：
1. 数字识别 ：如何识别整数、浮点数及负数？
2. 符号分离 ：如何避免将负号 - 错误地识别为减法操作符？

为此，可采用有限状态自动机的思想，在遍历字符串时维护当前“解析状态”。初始状态为空闲态，一旦读取到数字或负号后接数字，则切换至“数字收集状态”，持续读取直到非数字字符为止。

以下是一个简化的 C++ 实现示例，展示基本的词法切分逻辑：

enum TokenType {
    NUMBER,
    OPERATOR,
    LEFT_PAREN,
    RIGHT_PAREN,
    END_OF_EXPR
};

struct Token {
    TokenType type;
    std::string value; // 存储原始字符串表示
    double numValue;   // 若为数字，缓存其 double 值
};

std::vector<Token> tokenize(const std::string& expr) {
    std::vector<Token> tokens;
    size_t i = 0;
    while (i < expr.length()) {
        char c = expr[i];

        if (isspace(c)) {
            i++;
            continue;
        }

        if (isdigit(c) || (c == '-' && i + 1 < expr.length() && isdigit(expr[i + 1]))) {
            size_t start = i;
            if (c == '-') i++; // 负号计入数字部分
            while (i < expr.length() && (isdigit(expr[i]) || expr[i] == '.'))
                i++;
            std::string numStr = expr.substr(start, i - start);
            tokens.push_back({NUMBER, numStr, std::stod(numStr)});
        }
        else if (c == '+' || c == '-' || c == '*' || c == '/' || c == '^') {
            tokens.push_back({OPERATOR, std::string(1, c), 0});
            i++;
        }
        else if (c == '(') {
            tokens.push_back({LEFT_PAREN, "(", 0});
            i++;
        }
        else if (c == ')') {
            tokens.push_back({RIGHT_PAREN, ")", 0});
            i++;
        }
        else {
            throw std::runtime_error("非法字符: " + std::string(1, c));
        }
    }
    tokens.push_back({END_OF_EXPR, "", 0}); // 结束标记
    return tokens;
}

代码逻辑逐行解读与参数说明

• 第6–8行 ：跳过空白字符，提升输入容错性。
• 第10–18行 ：检测是否为数字或负数开头。条件 (c == '-' && ...) 判断负号后是否紧跟数字，防止将单独的 - 误判为负数。
• 第12–15行 ：使用 while 循环收集所有连续的数字和小数点，构成完整数值字符串。
• 第16–17行 ：调用 std::stod 将字符串转为 double 并缓存，便于后续计算。
• 第19–22行 ：单字符运算符直接封装为 OPERATOR 类型 Token。
• 第23–26行 & 27–30行 ：分别处理左右括号。
• 第31–33行 ：对未知字符抛出异常，保证语法安全性。
• 第34行 ：添加结束标记，供后续解析器识别输入终止。

此方法虽简洁，但存在局限：无法处理科学计数法（如 1e-5 ）、多字符函数名（如 sin 、 log ）等扩展形式。未来可通过正则表达式或更复杂的状态转移模型加以增强。

4.1.2 使用std::stringstream进行数字提取的技巧

尽管 std::stod 可快速转换字符串为浮点数，但在词法分析过程中直接使用可能引发异常或精度丢失。相比之下， std::stringstream 提供了更强的控制能力，尤其适用于需要逐字符验证合法性的场景。

考虑如下改进版数字提取函数：

bool tryExtractNumber(const std::string& str, size_t& pos, Token& token) {
    std::stringstream ss;
    size_t start = pos;

    // 处理负号
    if (str[pos] == '-') ss << str[pos++];
    // 至少需要一个数字
    if (pos >= str.length() || !isdigit(str[pos])) 
        return false;

    while (pos < str.length() && (isdigit(str[pos]) || str[pos] == '.')) {
        ss << str[pos++];
    }

    double value;
    if (ss >> value) {
        token = {NUMBER, str.substr(start, pos - start), value};
        return true;
    }
    return false;
}

参数说明与执行逻辑分析

• str : 输入表达式字符串。
• pos : 引用传递的当前位置索引，函数内会更新。
• token : 输出参数，用于返回成功解析的 Token。
• 函数返回布尔值表示是否成功提取有效数字。

该函数的优势在于：
1. 显式控制字符读取流程；
2. 支持负号前置；
3. 自动跳过多余空格；
4. 可集成进更大的状态机中，实现更复杂的词法结构识别。

此外，结合 peek() 和 eof() 方法，还能实现前瞻判断，例如检测指数部分 e 或 E 是否存在，从而支持科学计数法。

下图展示了词法分析器在处理表达式时的状态转移过程（Mermaid 流程图）：

stateDiagram-v2
    [*] --> Idle
    Idle --> DigitStart: 遇到数字或'-'后跟数字
    Idle --> Operator: 遇到+,-,*,/,^
    Idle --> ParenLeft: 遇到(
    Idle --> ParenRight: 遇到)
    Idle --> SkipSpace: 遇到空格
    DigitStart --> CollectingDigit: 开始收集数字字符
    CollectingDigit --> CollectingDigit: 继续读取数字或.
    CollectingDigit --> EmitNumber: 遇到非数字字符
    EmitNumber --> Idle
    SkipSpace --> Idle
    Operator --> Idle
    ParenLeft --> Idle
    ParenRight --> Idle

该状态图清晰表达了词法分析器内部的状态流转机制，有助于理解不同输入条件下行为差异，也为后续调试和扩展提供可视化支撑。

4.2 运算符优先级表的结构化定义

在表达式解析中，运算符的优先级和结合性决定了计算顺序。例如， * 的优先级高于 + ，而 ^ 是右结合的，即 2^3^2 = 2^(3^2) 。若缺乏统一的优先级管理体系，Shunting-yard 等算法将难以正确调度操作符入栈时机。

因此，必须建立一张 结构化的优先级表 ，将每个运算符映射为其对应的优先级数值和结合方向。这不仅能提高代码可读性，还便于后期扩展新运算符（如 % 、 && 、 || 等）。

4.2.1 哈希表映射优先级数值的C++实现方式

最自然的选择是使用 std::unordered_map<std::string, int> 来存储运算符与其优先级之间的映射关系。然而，仅记录优先级不足以处理结合性问题，因此应进一步引入结构体封装。

enum Associativity {
    LEFT,
    RIGHT
};

struct OperatorInfo {
    int precedence;         // 优先级数值，越大越高
    Associativity assoc;    // 结合方向
};

std::unordered_map<std::string, OperatorInfo> opTable = {
    {"+", {1, LEFT}},
    {"-", {1, LEFT}},
    {"*", {2, LEFT}},
    {"/", {2, LEFT}},
    {"%", {2, LEFT}},
    {"^", {3, RIGHT}}  // 幂运算为右结合
};

参数说明与设计优势

• precedence : 数值越高，优先级越高。加减为1，乘除为2，幂为3。
• assoc : 决定相同优先级下的运算顺序。左结合从左向右（如 a - b - c ），右结合从右向左（如 a ^ b ^ c ）。

在 Shunting-yard 算法中，比较两个运算符时需综合判断：

bool shouldPopOperator(const std::string& stackOp, const std::string& currentOp) {
    auto it1 = opTable.find(stackOp);
    auto it2 = opTable.find(currentOp);

    if (it1 == opTable.end() || it2 == opTable.end())
        return false;

    int prec1 = it1->second.precedence;
    int prec2 = it2->second.precedence;

    if (prec1 > prec2) return true;
    if (prec1 < prec2) return false;

    // 相同优先级时看结合性
    return it1->second.assoc == LEFT;
}

上述函数用于决定是否应将栈顶操作符弹出并加入输出队列。只有当栈顶操作符优先级更高，或同等优先级且为左结合时才弹出。

这种设计极大增强了系统的可配置性和可维护性。新增运算符只需向 opTable 添加条目即可，无需修改核心逻辑。

4.2.2 结合方向（左/右）的枚举标记与决策影响

结合性直接影响表达式的求值路径。以 2 ^ 3 ^ 4 为例：

• 若按左结合： (2 ^ 3) ^ 4 = 8 ^ 4 = 4096
• 若按右结合： 2 ^ (3 ^ 4) = 2 ^ 81 ≈ 2.4e24

显然，数学上幂运算是右结合的，因此必须在优先级表中标注 RIGHT 。

下表列出常见运算符的优先级与结合性对照：

运算符	优先级	结合性	示例
^	3	右	a^b^c = a^(b^c)
* / %	2	左	a*b*c = (a*b)*c
+ -	1	左	a-b-c = (a-b)-c

该表格不仅可用于文档说明，也可作为测试用例的设计依据。

以下为 Mermaid 表格展示：

table
    | 运算符 | 优先级 | 结合性 |
    |--------|--------|--------|
    | ^      | 3      | 右     |
    | * / %  | 2      | 左     |
    | + -    | 1      | 左     |

通过将结合性纳入优先级判断逻辑，我们实现了对标准数学规则的精确建模，确保生成的后缀表达式符合预期。

4.3 Token类的封装与类型系统构建

在大型表达式解析系统中，原始字符串和数值混合存储的需求促使我们必须设计一个类型安全的 Token 类。传统的 union 方式虽节省空间，但易引发未定义行为；现代 C++ 推荐使用 std::variant 实现类型安全的“代数数据类型”。

4.3.1 枚举类型标识数字、运算符、括号等类别

首先定义 TokenType 枚举，明确所有可能的 Token 种类：

enum class TokenType {
    NUMBER,
    OPERATOR,
    LEFT_PAREN,
    RIGHT_PAREN,
    FUNCTION,     // 如 sin, cos
    COMMA,        // 函数参数分隔符
    UNKNOWN
};

此强类型枚举避免了命名冲突，并支持编译期检查。

4.3.2 联合体（union）或变体（std::variant）存储不同值

传统做法使用 union ：

union TokenValue {
    double number;
    std::string* op; // 注意：需手动管理生命周期
};

但 union 不支持构造函数和析构函数，极易导致资源泄漏。

推荐使用 std::variant ：

using TokenValue = std::variant<double, std::string>;

struct Token {
    TokenType type;
    TokenValue value;
    size_t position; // 记录原始位置，便于报错定位

    // 辅助函数
    bool isNumber() const { return type == TokenType::NUMBER; }
    double getNumber() const { return std::get<double>(value); }
    std::string getOperator() const { return std::get<std::string>(value); }
};

优势说明

• std::variant 类型安全，访问前可使用 std::holds_alternative 判断；
• 支持异常安全的拷贝与移动；
• 与 std::visit 配合实现多态行为。

示例访问代码：

void printToken(const Token& t) {
    std::visit([&](const auto& val) {
        using T = std::decay_t<decltype(val)>;
        if constexpr (std::is_same_v<T, double>)
            std::cout << "Number: " << val << "\n";
        else
            std::cout << "String: " << val << "\n";
    }, t.value);
}

该设计使得 Token 成为真正意义上的通用容器，既能承载数值又能表示符号，同时保留位置信息用于错误报告。

4.4 模块间接口设计与数据传递契约

一个良好的系统架构要求各模块之间有清晰的数据接口。Lexer 的输出必须严格满足 Parser（如 Shunting-yard）的输入需求，否则会导致运行时崩溃或逻辑错误。

4.4.1 Lexer输出与Shunting-yard输入的数据格式一致性

Shunting-yard 算法依赖于以下假设：
- 所有 Token 已正确分类；
- 数字已转换为 double ；
- 运算符以字符串形式提供；
- 括号明确标记。

因此，Lexer 必须保证输出的 std::vector<Token> 满足这些前提。为此，可在头文件中定义公共接口规范：

// lexer.h
std::vector<Token> lex(const std::string& expression);
// 抛出 std::invalid_argument 表示词法错误

Parser 层只需信任输入的 Token 序列类型正确，无需重复验证。

4.4.2 异常安全的Token序列生成保障机制

为提升鲁棒性，应在 Lexer 中实现两级校验：
1. 词法层校验 ：拒绝非法字符、不完整数字（如 3. ）、孤立小数点；
2. 语法层提示 ：记录每个 Token 的起始位置，便于错误定位。

例如：

try {
    auto tokens = lex(input);
} catch (const std::exception& e) {
    std::cerr << "词法错误 at position X: " << e.what() << "\n";
}

通过定义统一的异常层次结构（如继承自 ParseError ），可在整个系统中实现一致的错误传播机制。

综上所述，Lexer 不仅是解析链的第一环，更是保障整体系统稳定性的基石。通过精细化的 Token 设计、结构化的优先级管理以及严格的接口契约，我们为后续的语法分析与求值奠定了坚实基础。

5. 完整表达式解析系统的集成与健壮性优化

5.1 多模块协同工作的主控函数架构

在完成词法分析、中缀转后缀、后缀求值等核心模块后，构建一个端到端的表达式解析系统需要设计清晰的主控流程。该流程应实现从原始字符串输入到最终数值输出的无缝衔接，并具备良好的错误传播机制。

以下是一个典型的主控函数结构示例：

#include <iostream>
#include <string>
#include <vector>
#include <stdexcept>
#include "Lexer.h"      // Token定义与词法分析器
#include "ShuntingYard.h"  // 中缀转后缀算法
#include "Evaluator.h"     // 后缀表达式求值器

enum class ParseError {
    None,
    LexicalError,
    MismatchedParentheses,
    InvalidTokenSequence,
    EvaluationError
};

// 主控函数：集成所有模块
double evaluateExpression(const std::string& expr, ParseError& error) {
    error = ParseError::None;

    try {
        // 阶段1：词法分析
        Lexer lexer(expr);
        std::vector<Token> tokens;
        if (!lexer.tokenize(tokens)) {
            error = ParseError::LexicalError;
            return 0.0;
        }

        // 阶段2：语法检查 - 括号匹配
        int parenCount = 0;
        for (const auto& token : tokens) {
            if (token.type == TokenType::LEFT_PAREN) parenCount++;
            else if (token.type == TokenType::RIGHT_PAREN) parenCount--;
            if (parenCount < 0) {
                error = ParseError::MismatchedParentheses;
                return 0.0;
            }
        }
        if (parenCount != 0) {
            error = ParseError::MismatchedParentheses;
            return 0.0;
        }

        // 阶段3：转换为后缀表达式
        std::vector<Token> postfix;
        if (!shuntingYard(tokens, postfix)) {
            error = ParseError::InvalidTokenSequence;
            return 0.0;
        }

        // 阶段4：求值
        double result = evaluatePostfix(postfix, error);
        if (error != ParseError::None) {
            return 0.0;
        }

        return result;
    } catch (const std::exception&) {
        error = ParseError::EvaluationError;
        return 0.0;
    }
}

上述代码展示了完整的处理流水线：
- 输入字符串经 Lexer 分解为 Token 序列；
- 在进入 Shunting-yard 算法前进行括号合法性预检；
- 使用独立函数 shuntingYard() 执行转换；
- 最终调用 evaluatePostfix() 得到结果。

各阶段通过 ParseError 枚举统一反馈错误类型，便于上层调用者进行差异化处理。

5.2 常见语法错误的检测与反馈机制

为了提升用户体验和调试效率，系统需对常见语法错误提供精准定位和可读性强的提示信息。

括号不匹配的计数器检测法

采用括号计数器法可在词法分析后立即检测括号结构完整性：

当前字符	Token 类型	计数器变化	错误状态判断
’(‘	LEFT_PAREN	+1	若计数器<0 → 提前闭合
’)’	RIGHT_PAREN	-1	若计数器<0 → 抛出异常
其他	——	不变	——

当遍历结束时若计数器 ≠ 0，则存在未闭合或多余左括号。

非法字符过滤与错误信息构造

可通过正则表达式或状态机预筛非法字符：

bool isValidChar(char c) {
    return std::isdigit(c) || c == '.' || 
           std::strchr("+-*/^()%", c) != nullptr || 
           std::isspace(c);
}

std::pair<bool, size_t> findFirstInvalidChar(const std::string& expr) {
    for (size_t i = 0; i < expr.length(); ++i) {
        if (!isValidChar(expr[i])) {
            return {false, i};  // 返回位置索引
        }
    }
    return {true, std::string::npos};
}

结合位置信息可生成如下提示：

错误：表达式第 7 个字符 'x' 是非法符号，请检查输入。

此机制显著增强了系统的容错性和交互友好性。

5.3 代码模块化与可维护性增强实践

为提高代码可读性和扩展性，推荐使用类封装分离关注点。

职责分离的类设计

class ExpressionEvaluator {
private:
    Lexer lexer;
    std::vector<Token> tokens;
    std::vector<Token> postfix;

public:
    explicit ExpressionEvaluator() = default;

    bool parse(const std::string& expr);
    double evaluate();
    std::string getLastError() const;
};

其中：
- parse() 负责执行 tokenize 和 shunting-yard；
- evaluate() 调用 evaluator 模块计算结果；
- 内部缓存中间数据以支持多次求值。

避免拷贝开销的最佳实践

使用 const std::vector<Token>& 传递大型结构：

bool shuntingYard(const std::vector<Token>& input, 
                  std::vector<Token>& output);

避免不必要的深拷贝，尤其在频繁调用场景下能显著提升性能。

5.4 C++标准库组件的综合高效运用

vector管理Token序列的优势

std::vector 提供连续内存存储，适合频繁遍历操作：

特性	优势说明
动态扩容	自动增长，无需手动管理内存
O(1)随机访问	支持快速索引查找
与算法库兼容	可直接配合 std::find , std::transform 等
移动语义优化	函数返回时避免复制

sstream在字符串-数值转换中的鲁棒性应用

相比 atof() 或 stoi() ， std::stringstream 更安全：

bool safeStrToDouble(const std::string& str, double& value) {
    std::stringstream ss(str);
    ss >> value;
    return !ss.fail() && ss.eof();  // 确保完全解析
}

它能识别科学计数法（如 1.23e-4 ），并防止部分匹配问题（如 "123abc" 被截断解析）。

此外，配合 std::locale 还可支持国际化数字格式（如千位分隔符）。

本文还有配套的精品资源，点击获取

简介：在C++编程中，数学表达式解析是一项重要且常见的任务，涉及中缀表达式到后缀表达式的转换及基于栈的求值。本项目实现一个支持括号和四则运算的简易计算器，采用逆波兰表达式（后缀表达式）转换算法（Shunting-yard算法）与栈结构完成表达式解析与计算。项目涵盖词法分析、优先级处理、负数与浮点数识别、错误检测等关键环节，适用于学习栈的应用、表达式求值原理及C++标准库（如std::stack、std::vector、std::istringstream）的实际使用。经过完整测试，该项目可作为数据结构与算法实践的经典案例。

本文还有配套的精品资源，点击获取