三折线弹塑性滞回模型matlab,某连体结构动力弹塑性分析报告-使用midas building

1.弹塑性动力时程分析的主要技术参数指标简述

1.1基于材料的本构模型

本工程混凝土本构关系采用《混凝土结构设计规范》GB50010-2010附录C中的单轴受压应力-应变本构模型，混凝土单轴受压应力-应变关系曲线如图1-1；钢筋采用双折线本构模型，如图1-2，屈服前后的刚度不同，屈服后的刚度使用折减后的刚度。无论屈服与否，卸载和重新加载时使用弹性刚度。剪切本构采用了理想弹塑性双折线模型，屈服前后的刚度不同，屈服前卸载和重新加载时使用弹性刚度；屈服后卸载时指向原点，重新加载时使用卸载刚度重新加载。如图1-3所示。

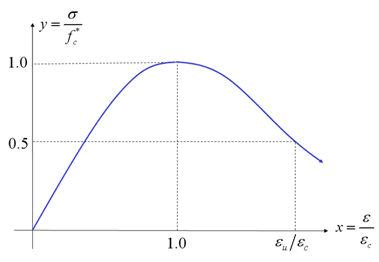
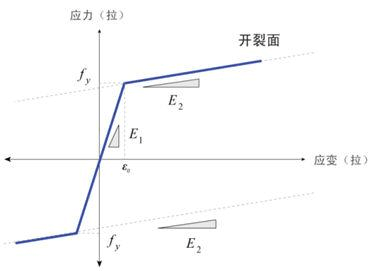
图1-1 混凝土单轴受压应力-应变曲线图1-2 双折线钢筋本构关系

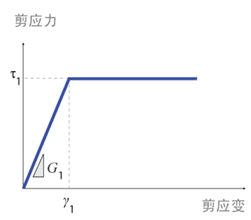
图1-3 理想弹塑性剪切本构模型

1.2基于截面的塑性铰滞回模型

滞回模型是动力弹塑性分析的基本参数，共有双折线、三折线、四折线等多种滞回模型。

本工程钢筋混凝土和型钢混凝土构件采用了修正武田三折线模型，如图

1-4所示，其仅考虑了刚度退化，没有考虑强度退化。第一折线拐点用于模拟开裂强度，第二个折线拐点用于模拟屈服强度，修正武田三折线模型对武田三折线模型的内环的卸载刚度计算方法做了修正。钢结构构件则采用了标准双折线滞回模型，卸载刚度使用弹性刚度，如图1-5所示。

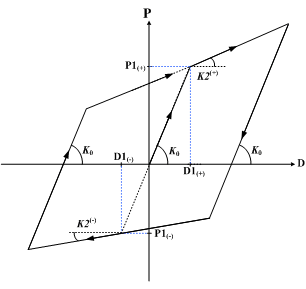
图1-4 修正武田三折线滞回模型图1-5 标准双折线滞回模型

1.3非线性梁柱单元

程序采用了具有非线性铰特性的梁柱单元。梁单元公式使用了柔度法(flexibility method)，在荷载作用下的变形和位移使用了小变形和平截面假定理论(欧拉贝努利梁理论，Euler Bernoulli Beam Theory)，并假设扭矩和轴力、弯矩成分互相独立无关联。非线性梁柱单元可考虑了P-Δ效应，在分析的每个步骤都会考虑内力对几何刚度的影响重新更新几何刚度矩阵，并将几