多叉树遍历 java_【LeetCode】429.N叉树的层序遍历（图文详解，三种方法，java实现）...

题目

分析

方法一：利用队列实现广度优先搜索

我们要构造一个 sub-lists 列表，其中每个 sub-list 是树中一行的值。行应该按从上到下的顺序排列。

因为我们从根节点开始遍历树，然后向下搜索最接近根节点的节点，这是广度优先搜索。我们使用队列来进行广度优先搜索，队列具有先进先出的特性。

在这里使用栈是错误的选择，栈应用于深度优先搜索。

让我们在树上使用基于队列的遍历算法，看看它的作用。这是你应该记住的一个基本算法。

List values = new ArrayList<>();

Queue queue = new LinkedList<>();

queue.add(root);

while (!queue.isEmpty()) {

Node nextNode = queue.remove();

values.add(nextNode.val);

for (Node child : nextNode.children) {

queue.add(child);

}

}

用一个列表存放节点值，队列存放节点。首先将根节点放到队列中，当队列不为空时，则在队列取出一个节点，并将其子节点添加到队列中。

让我们看看这个算法遍历树时我们得到了什么结果。

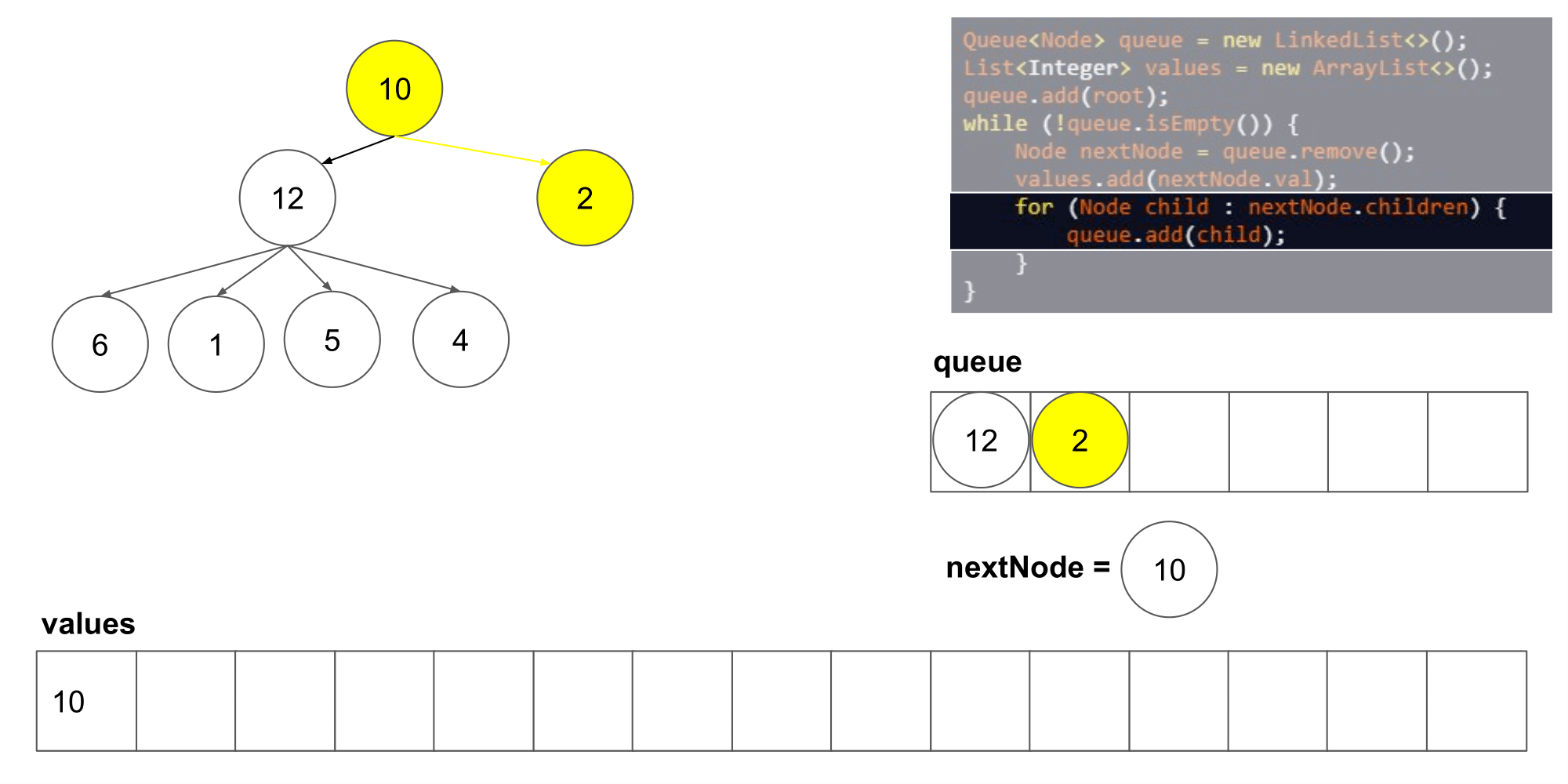
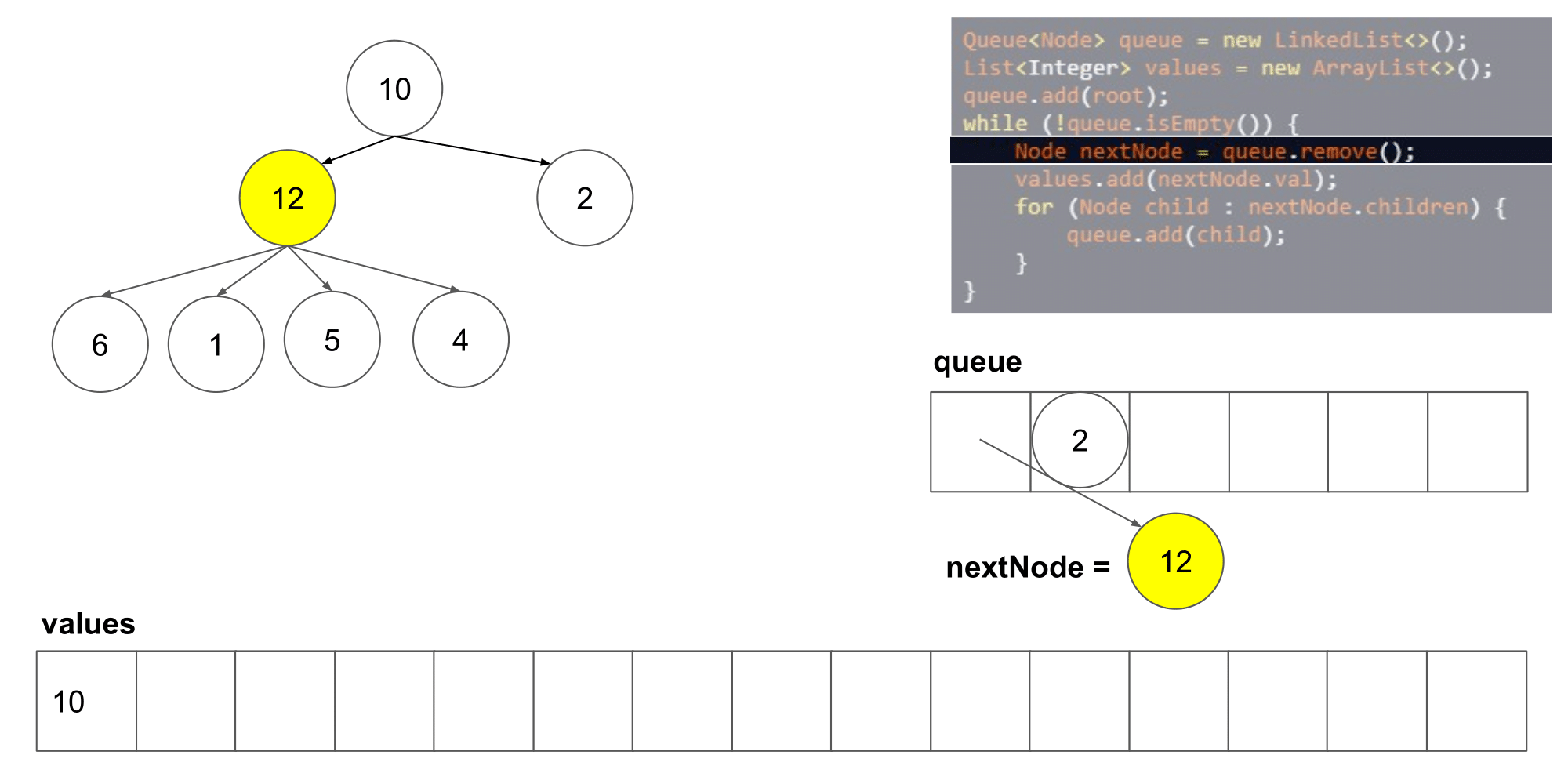
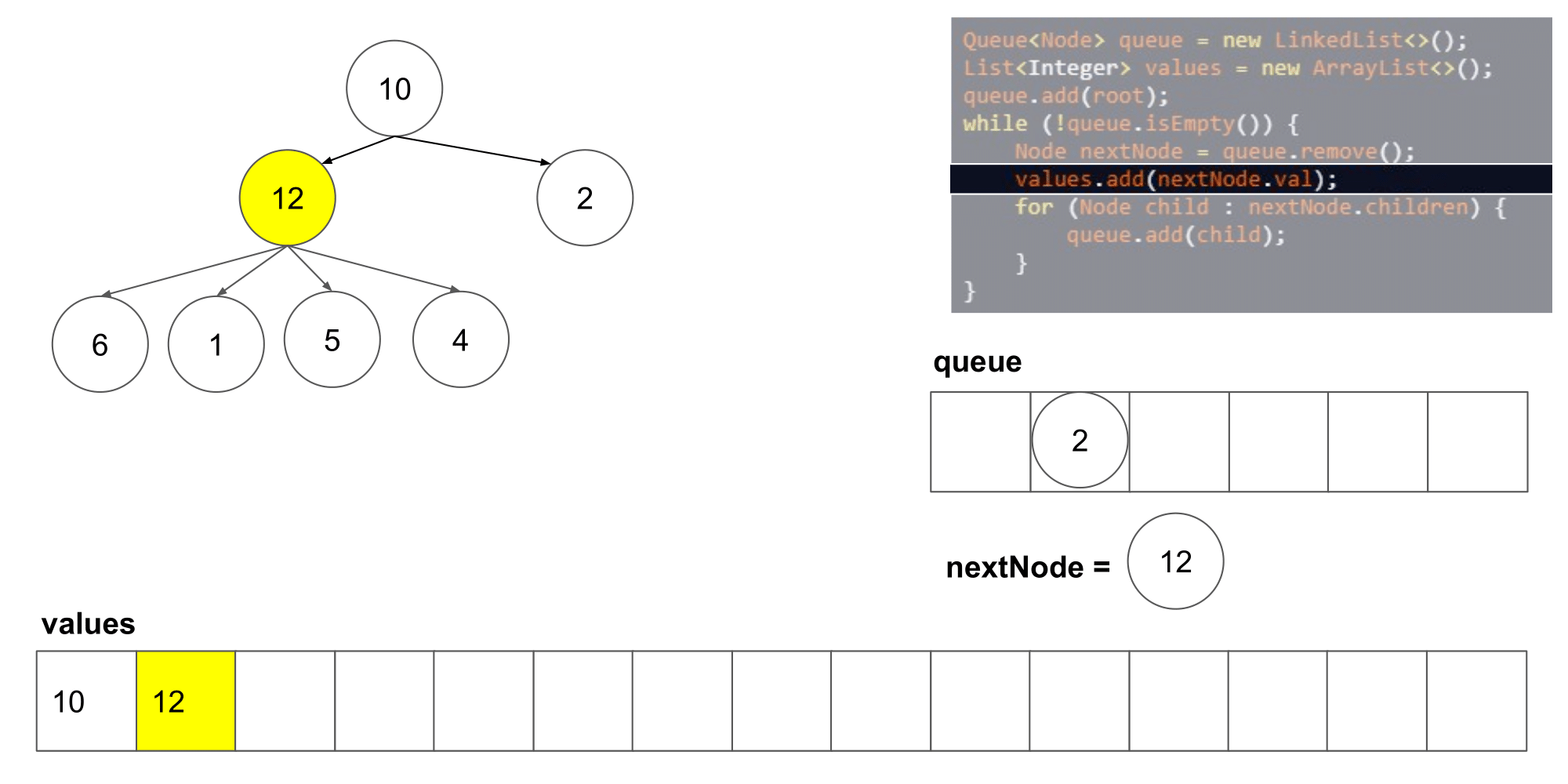
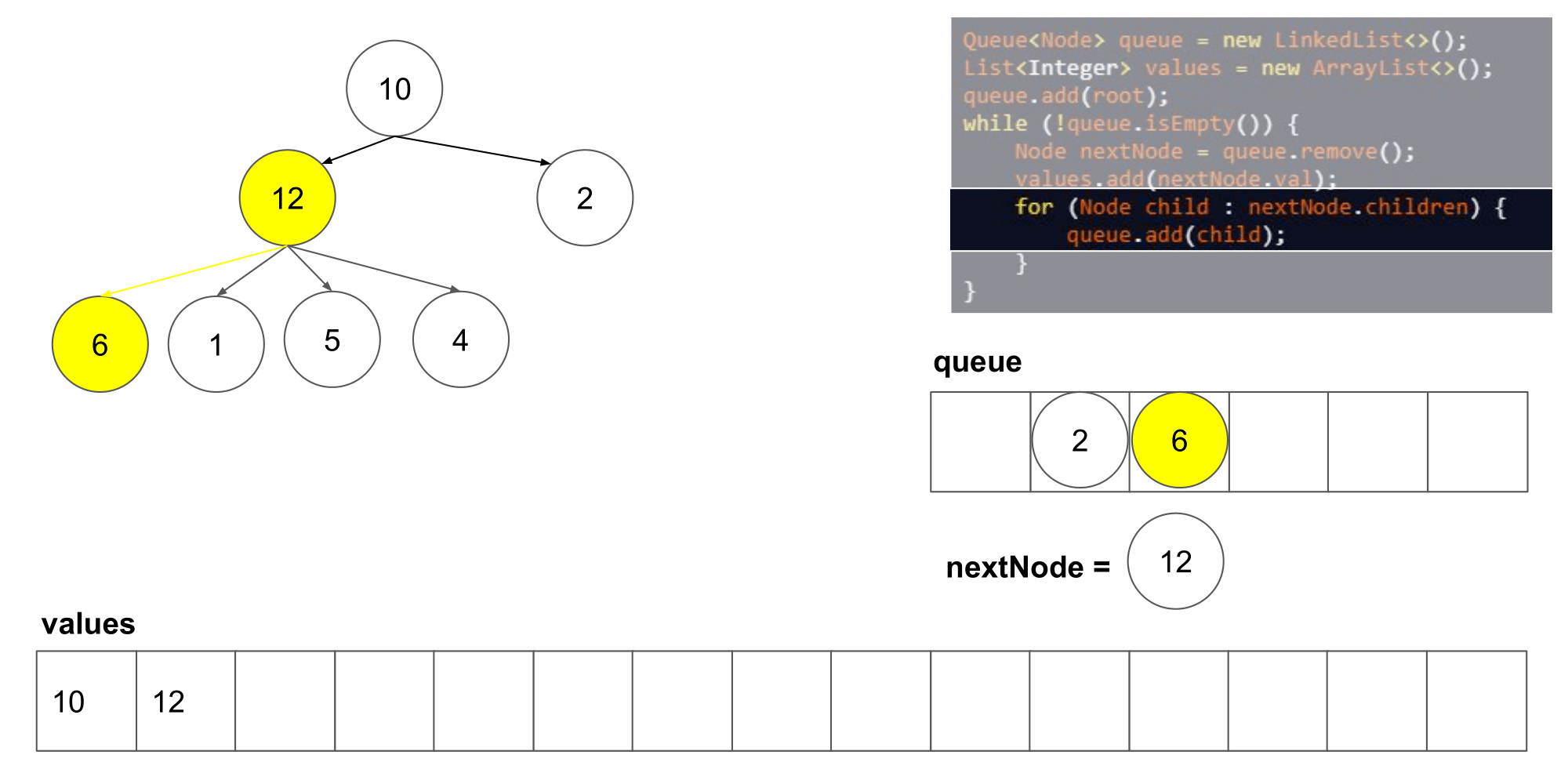
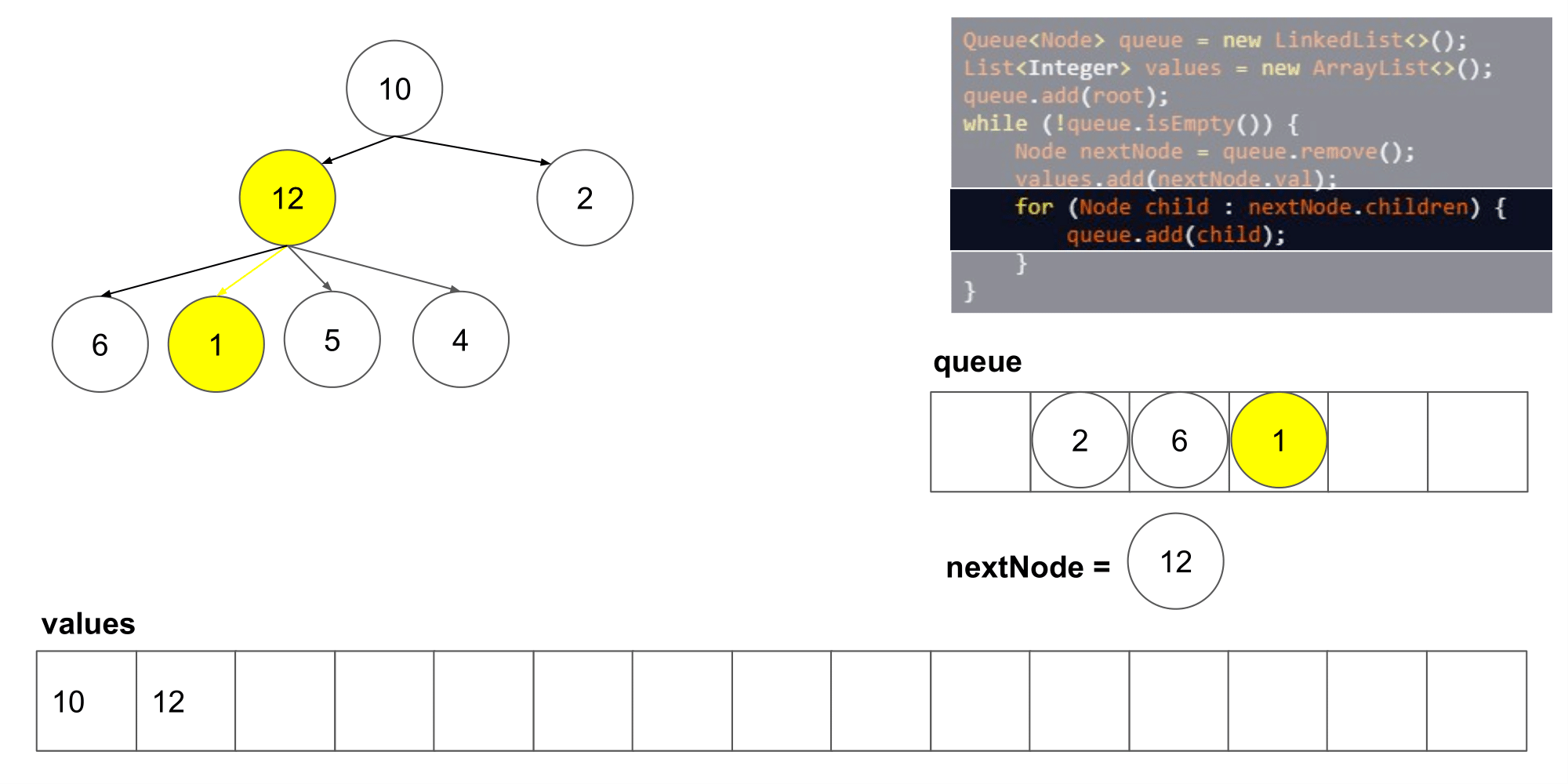
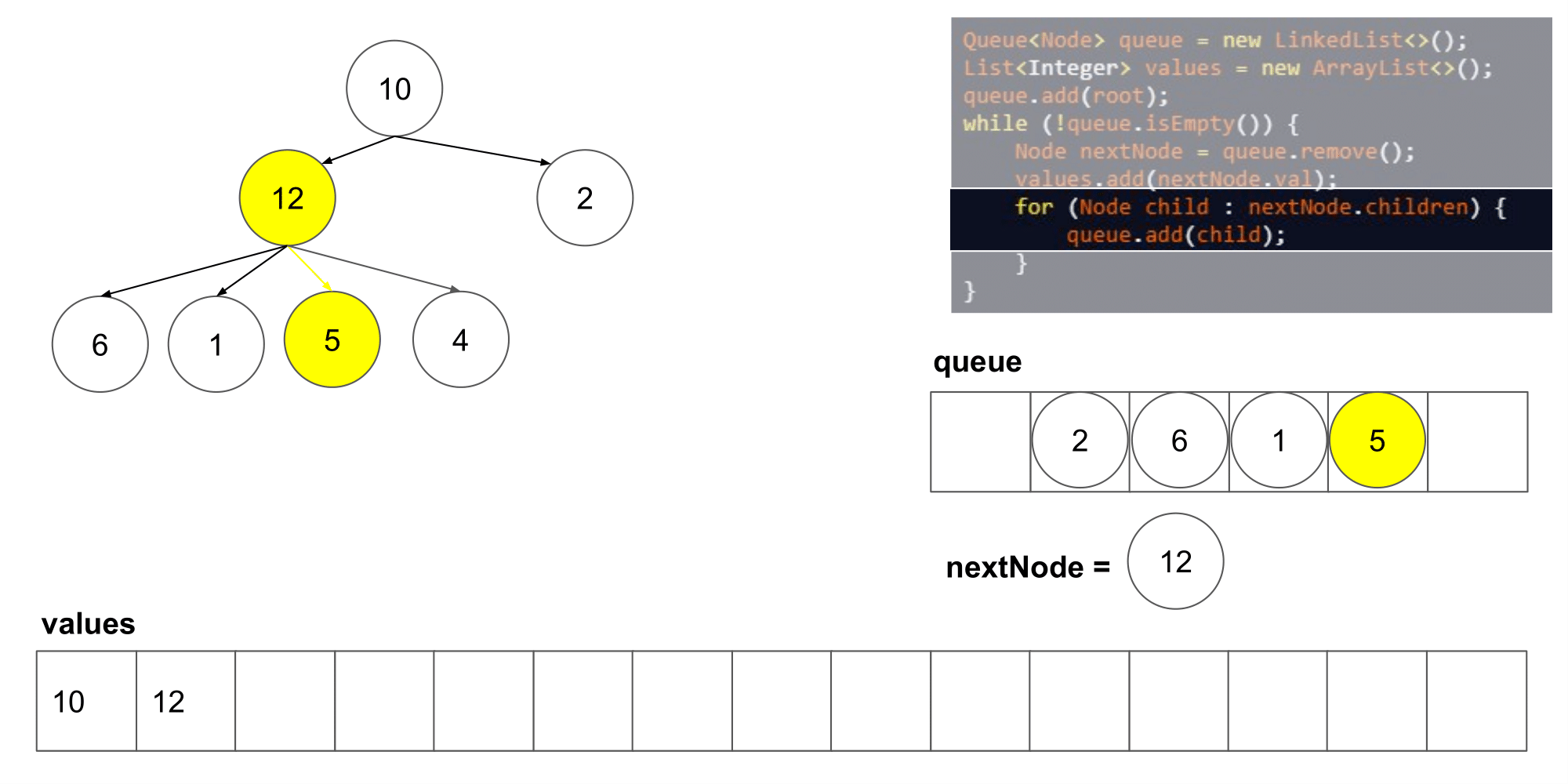
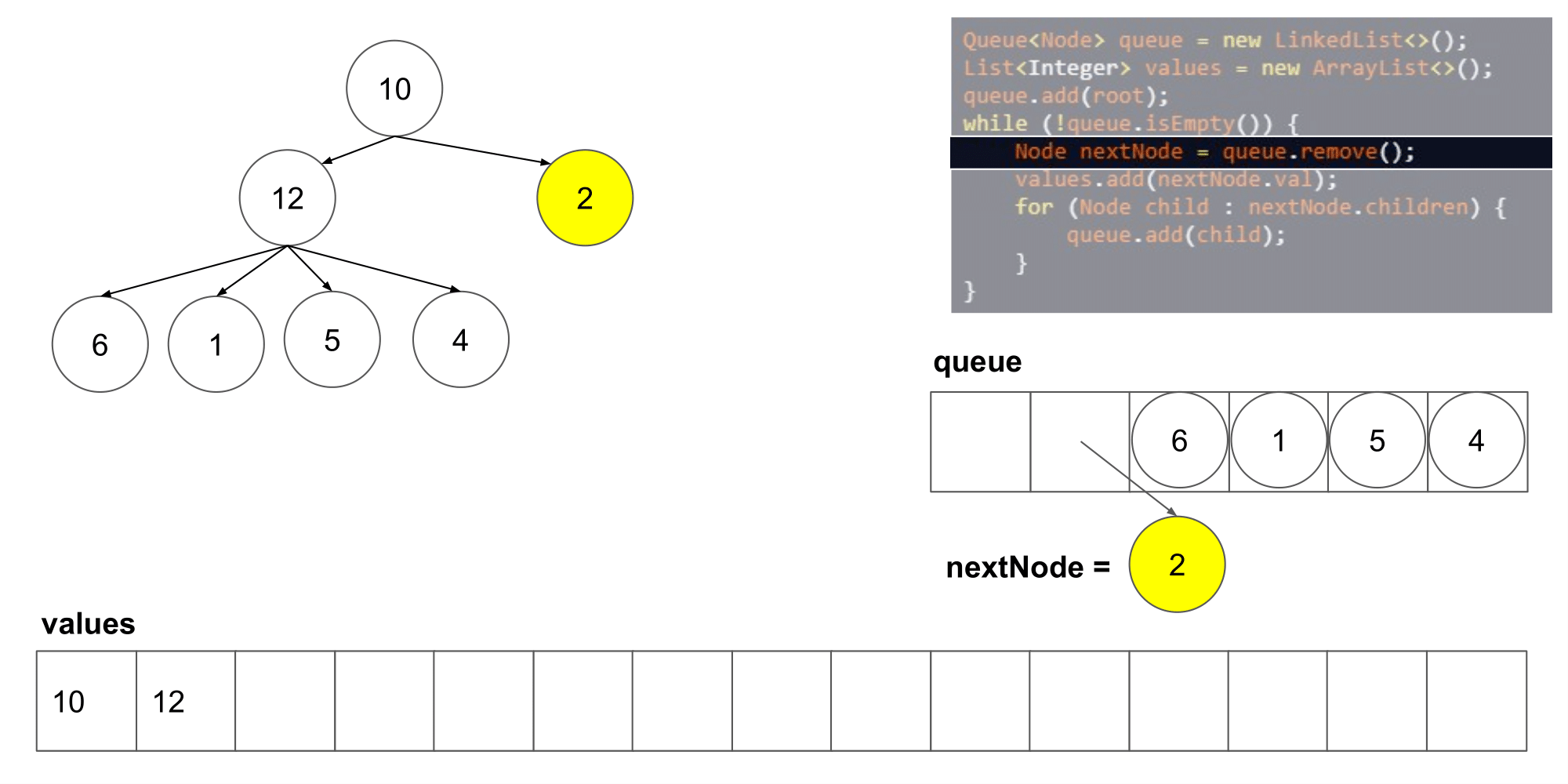
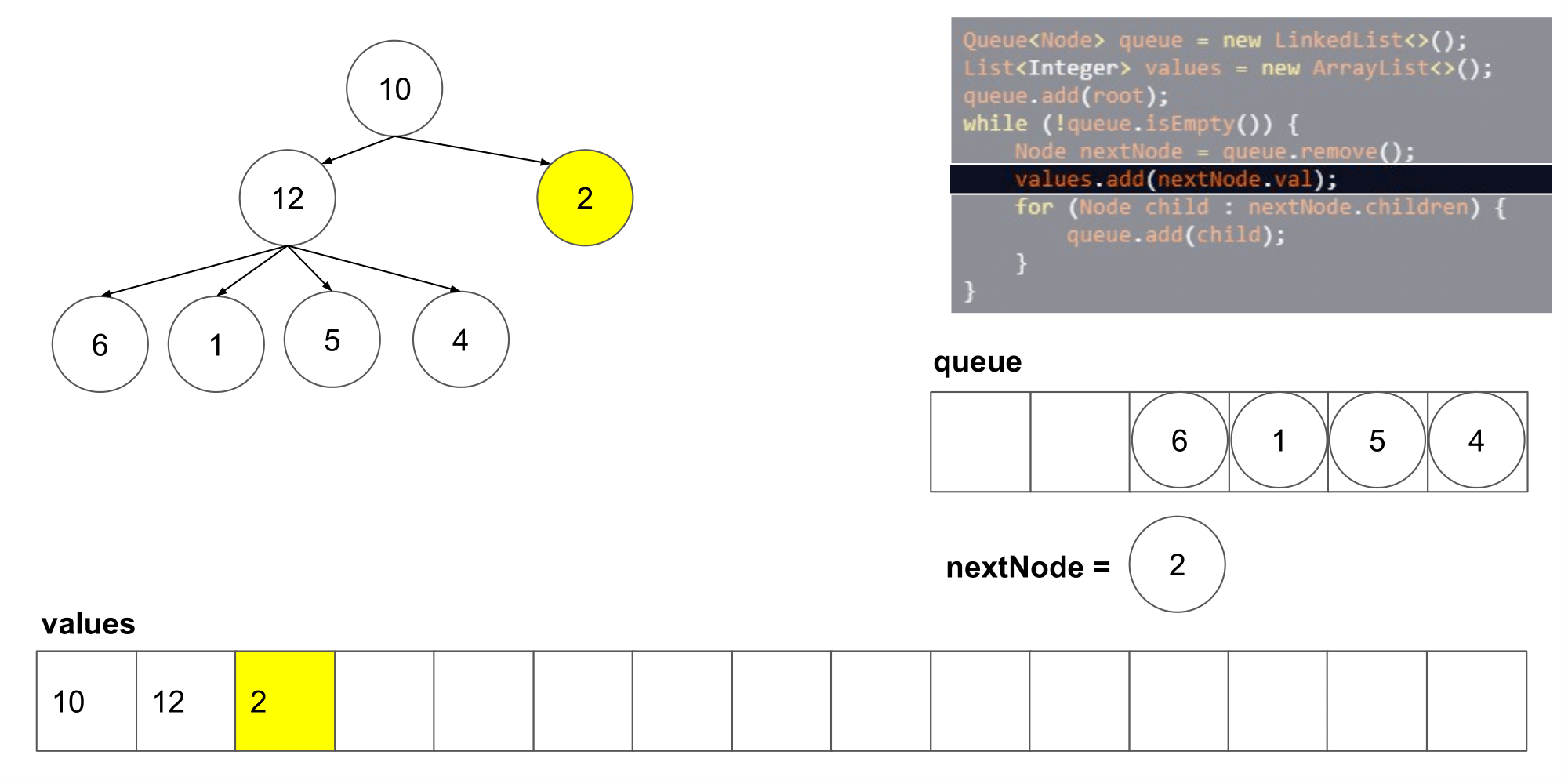
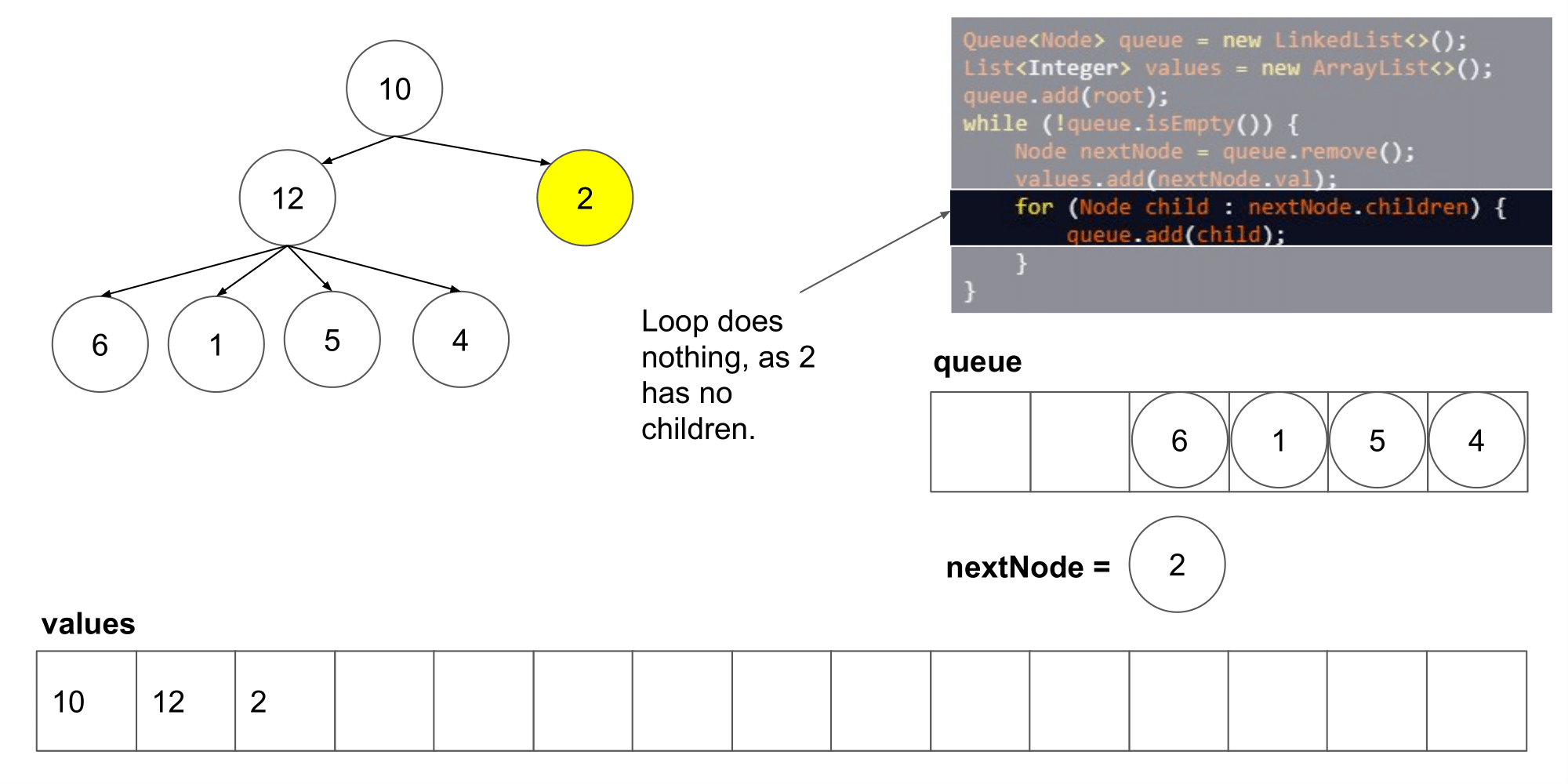
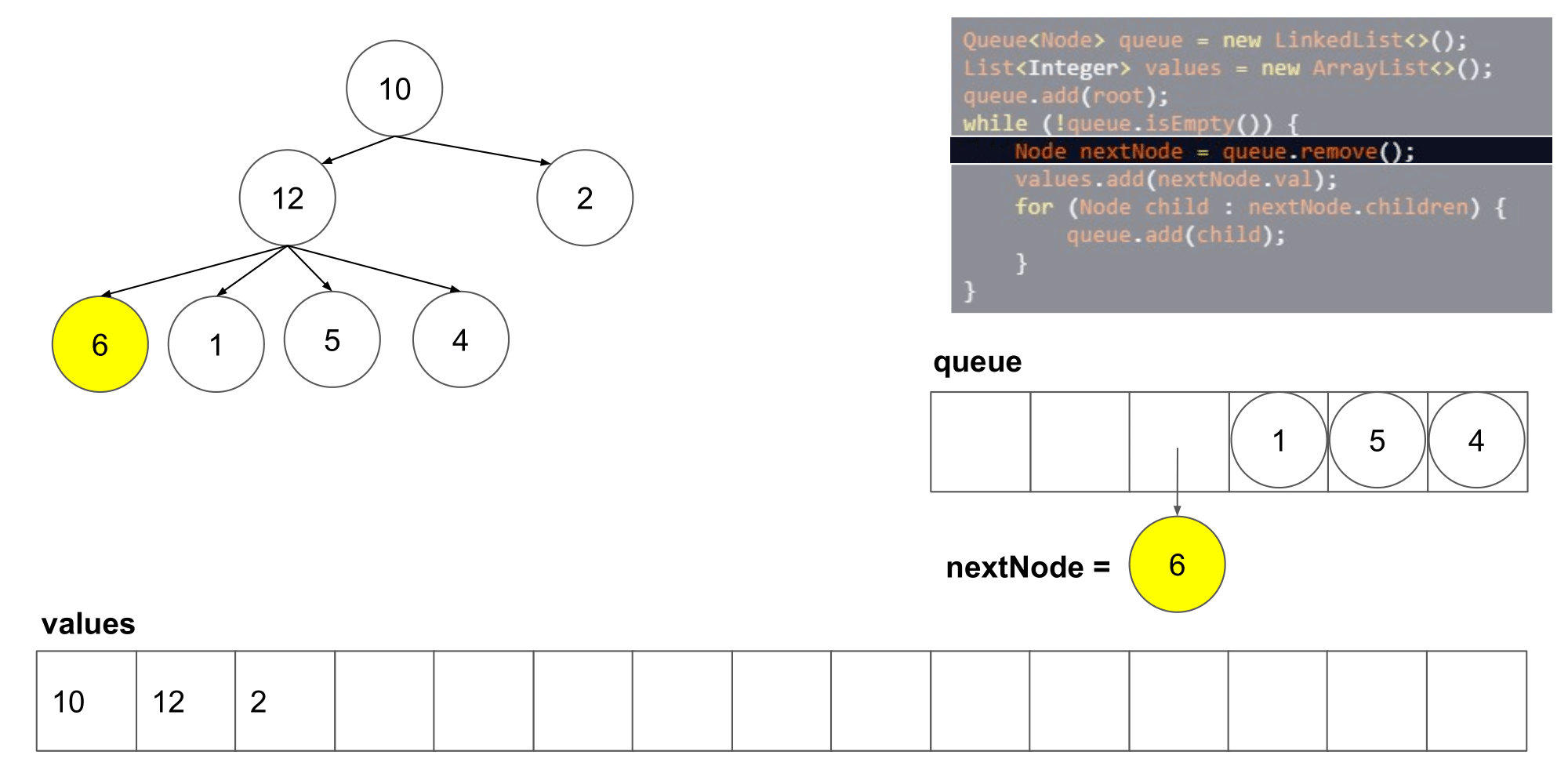
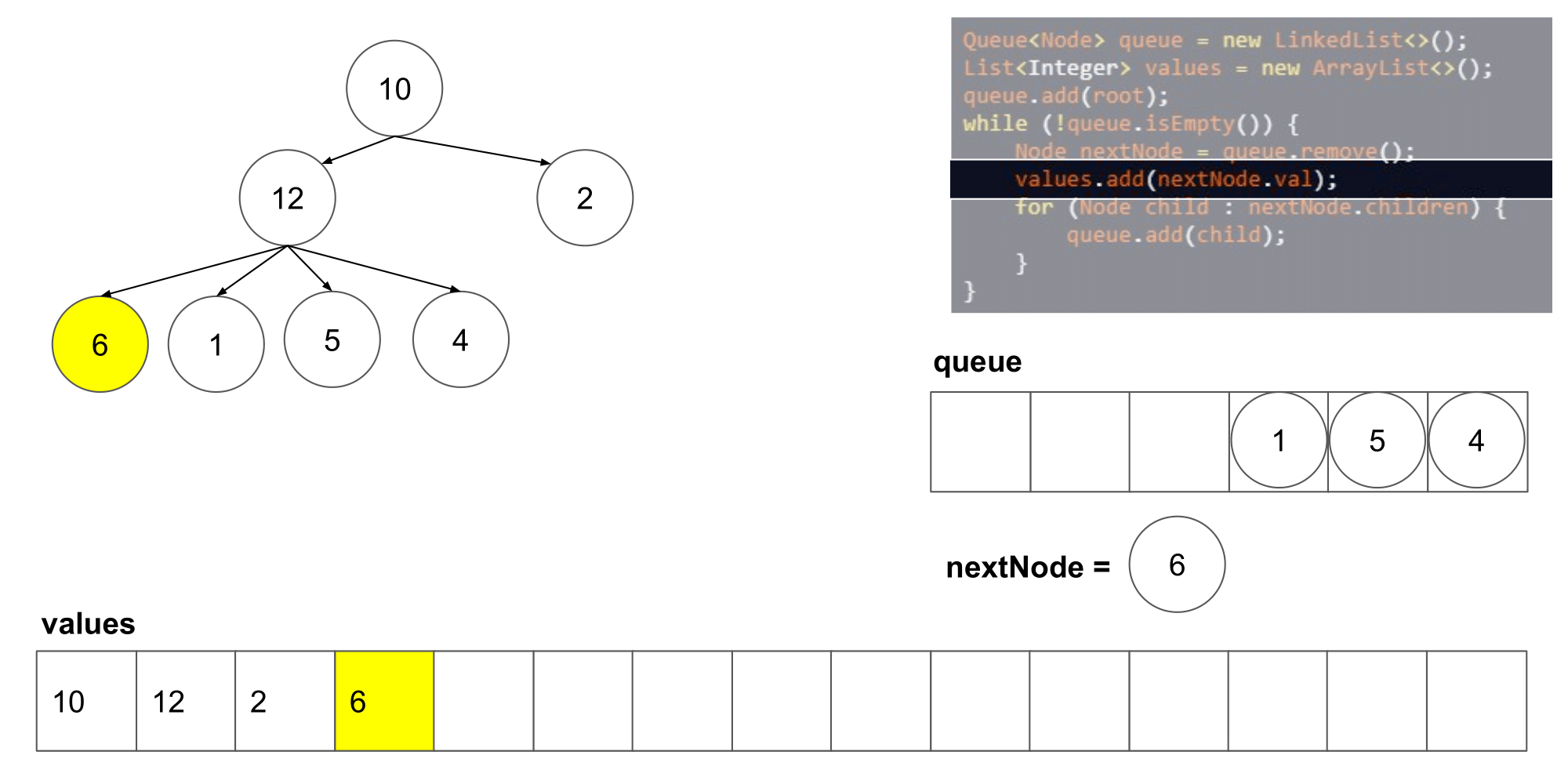
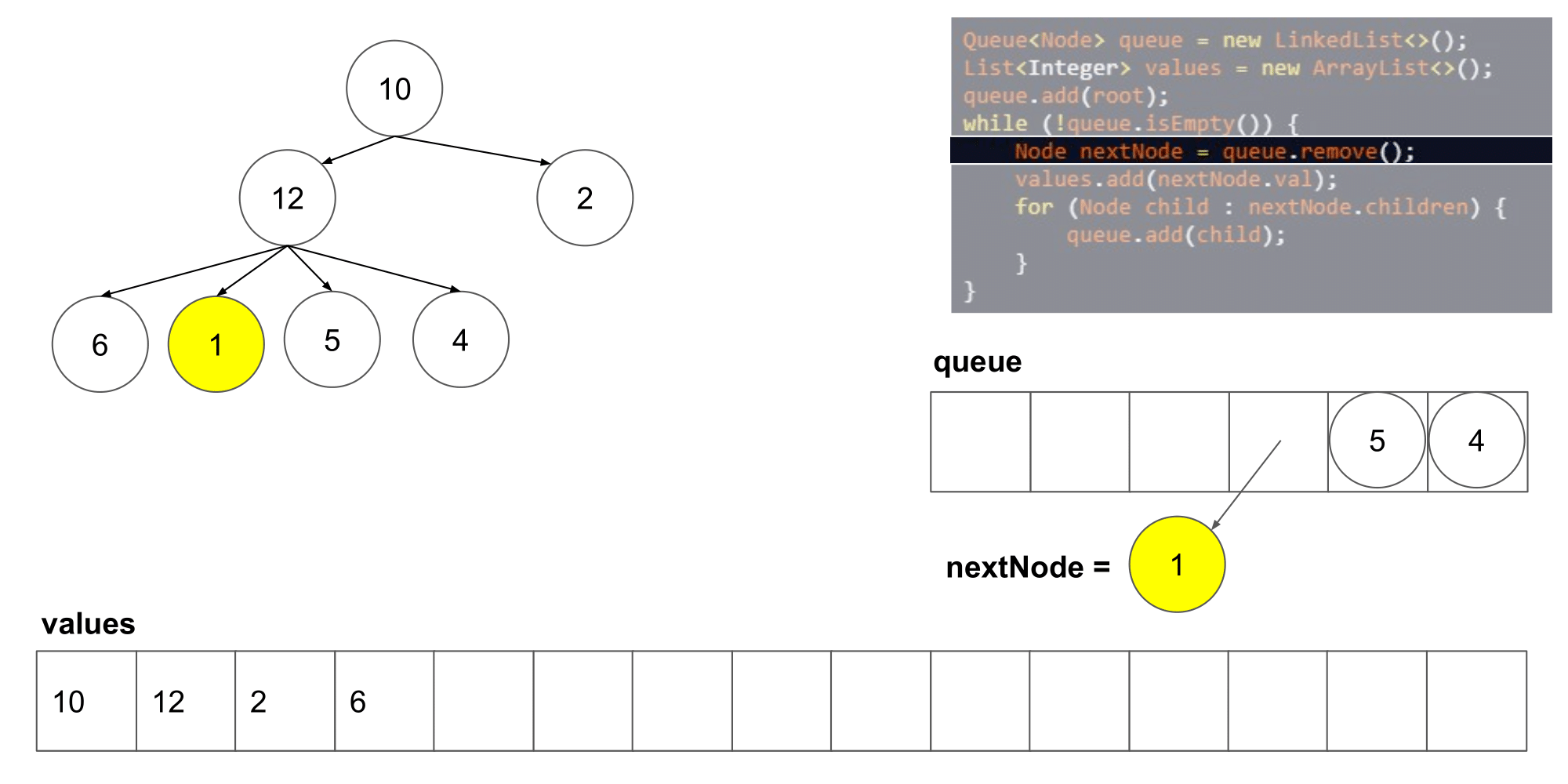
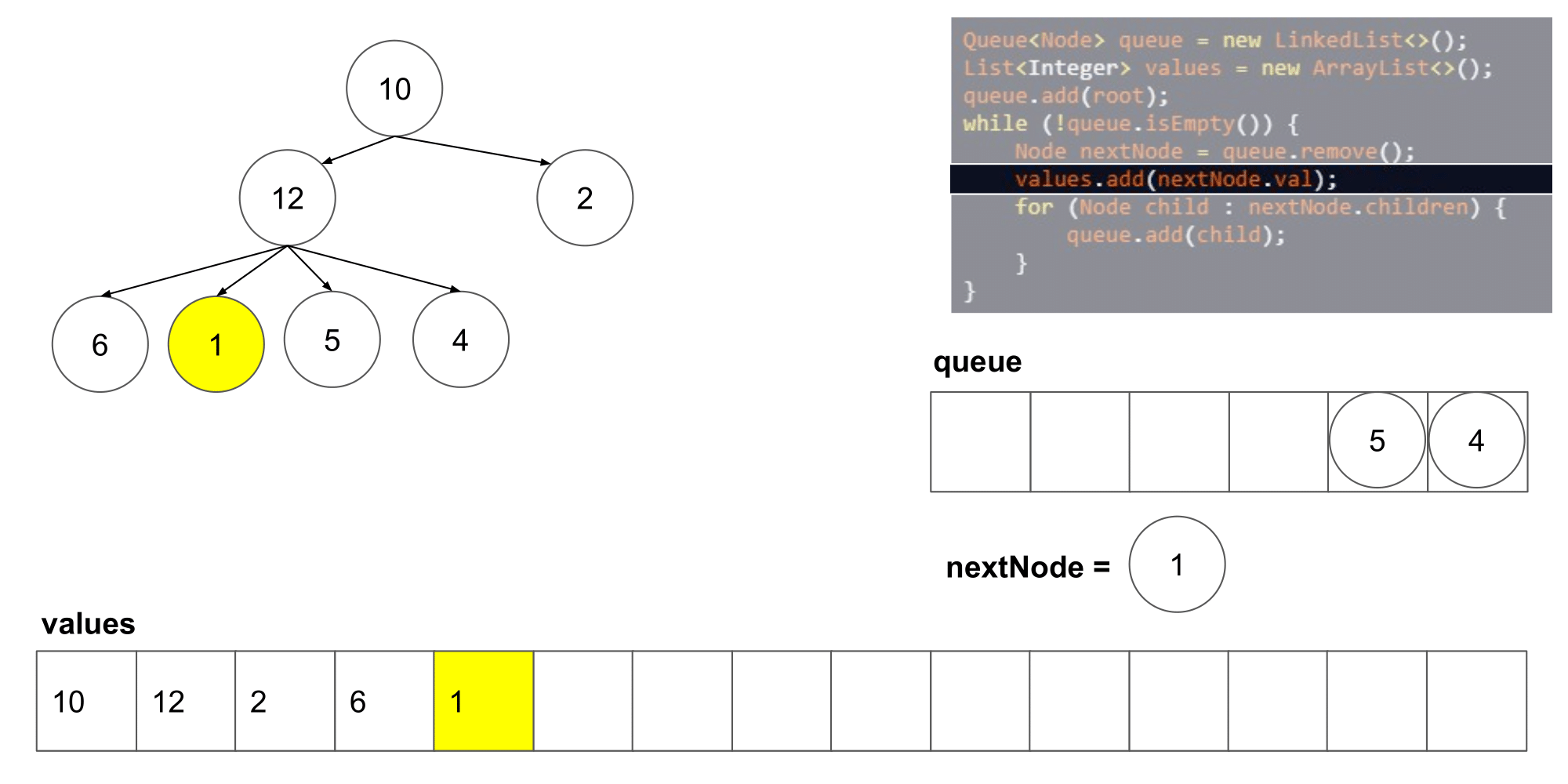
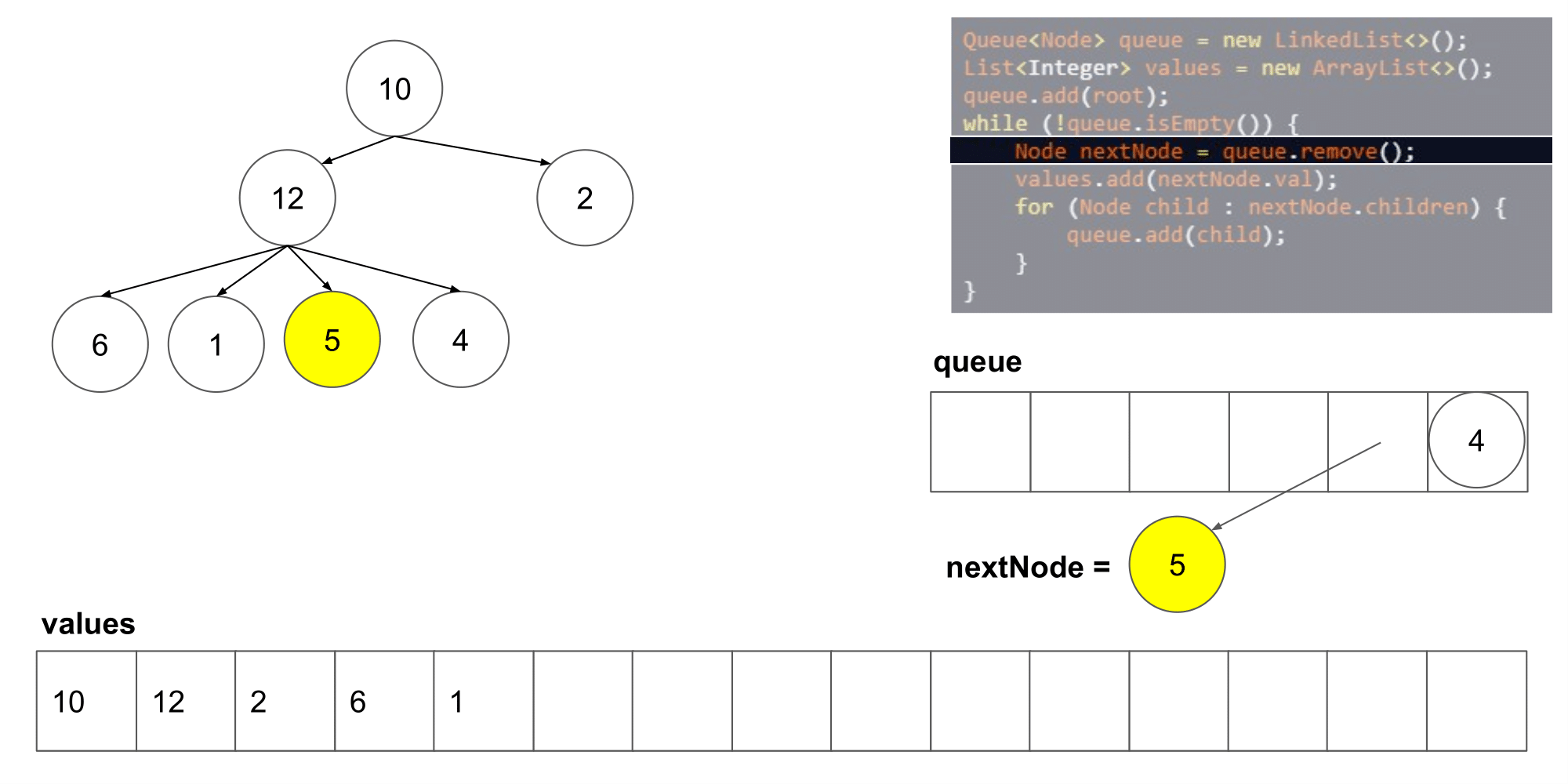
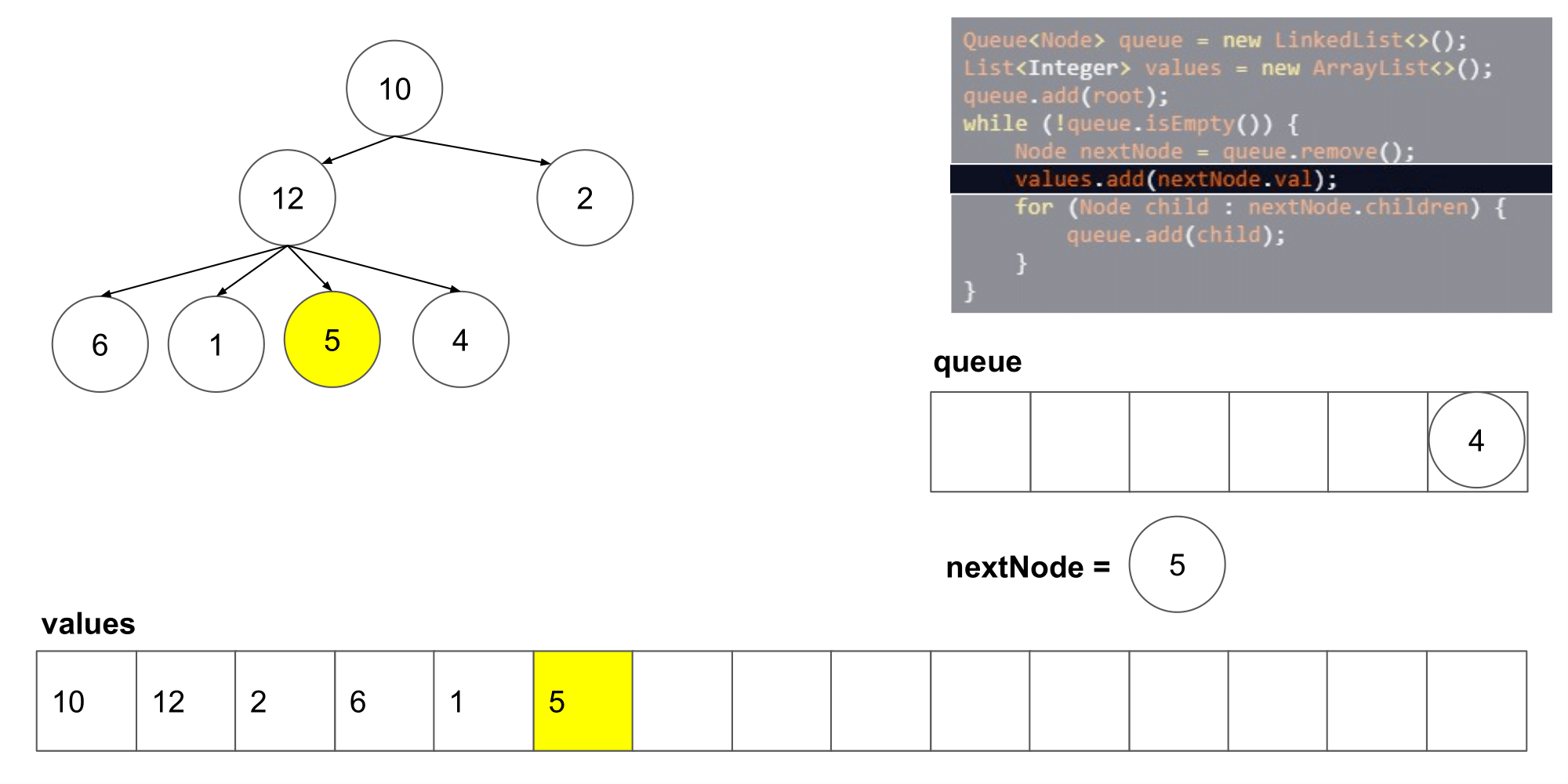
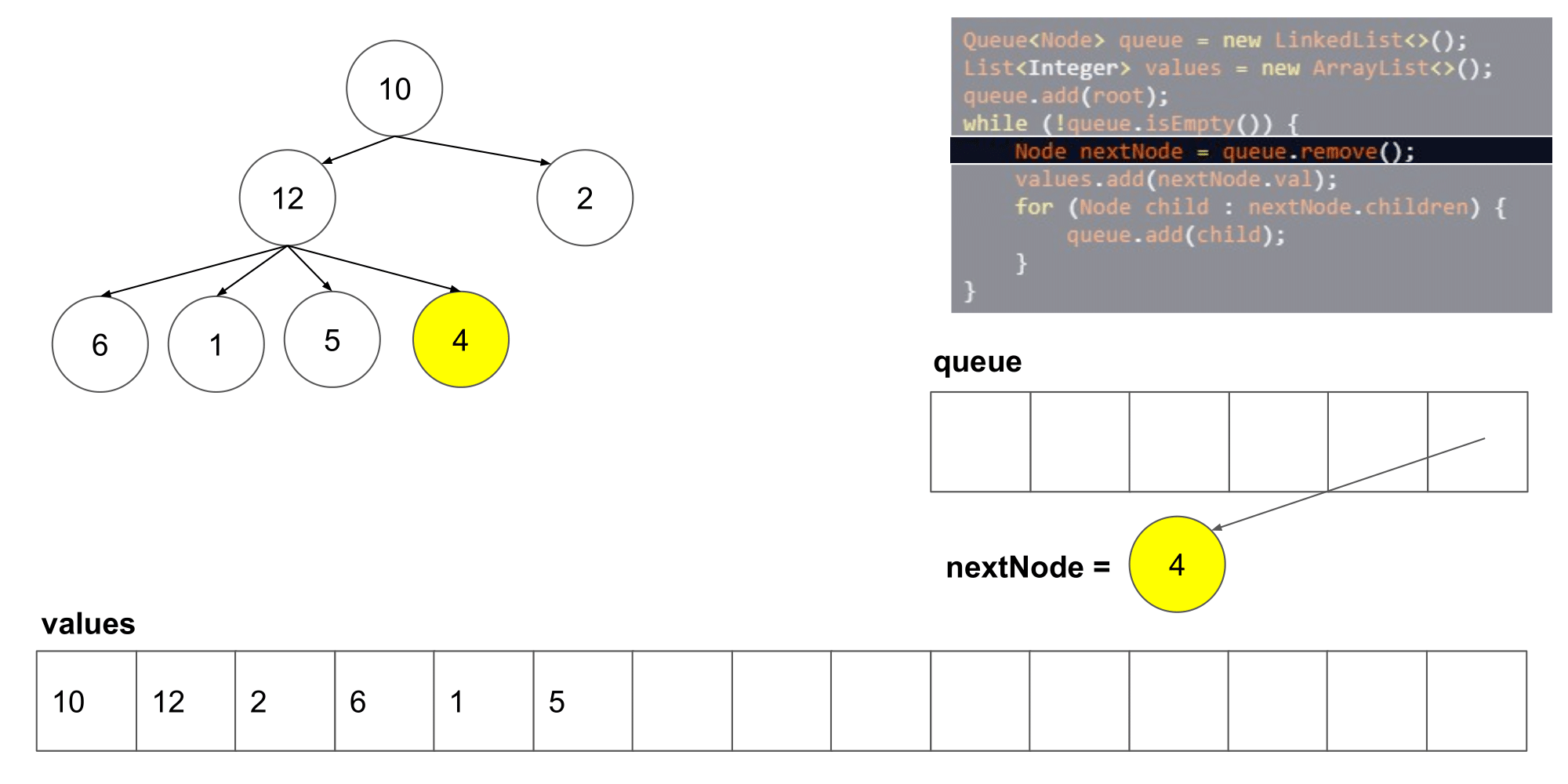
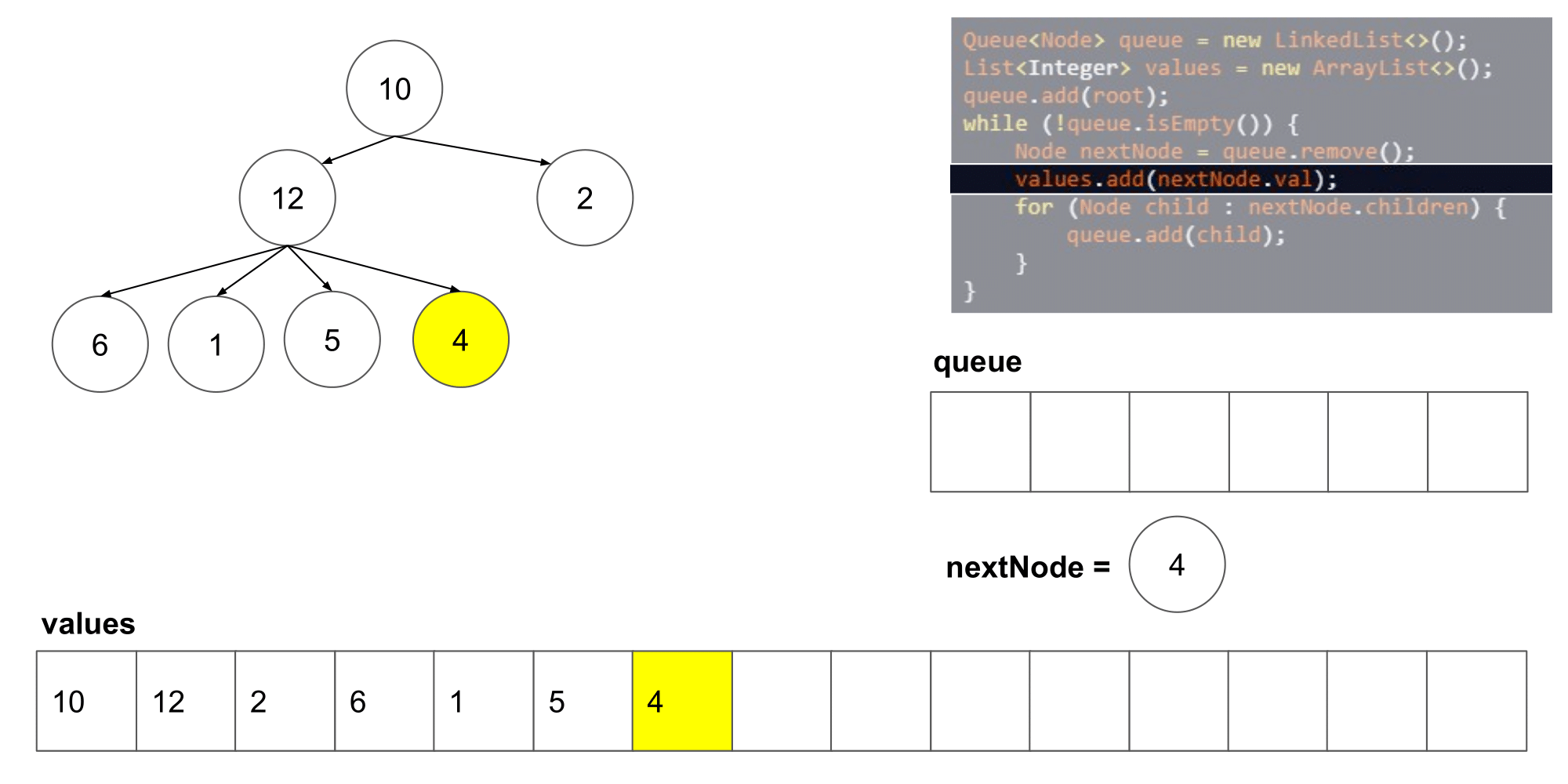
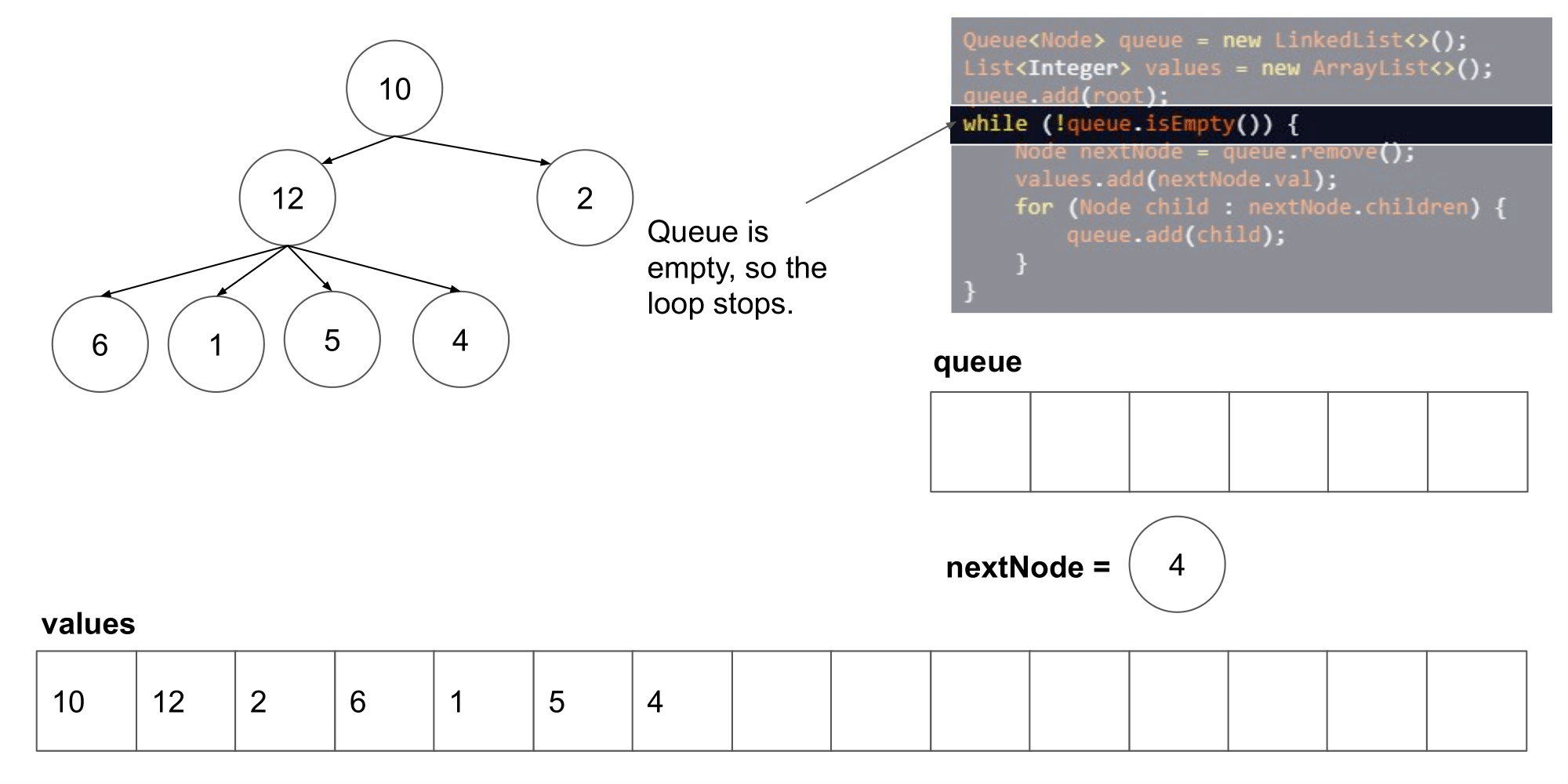
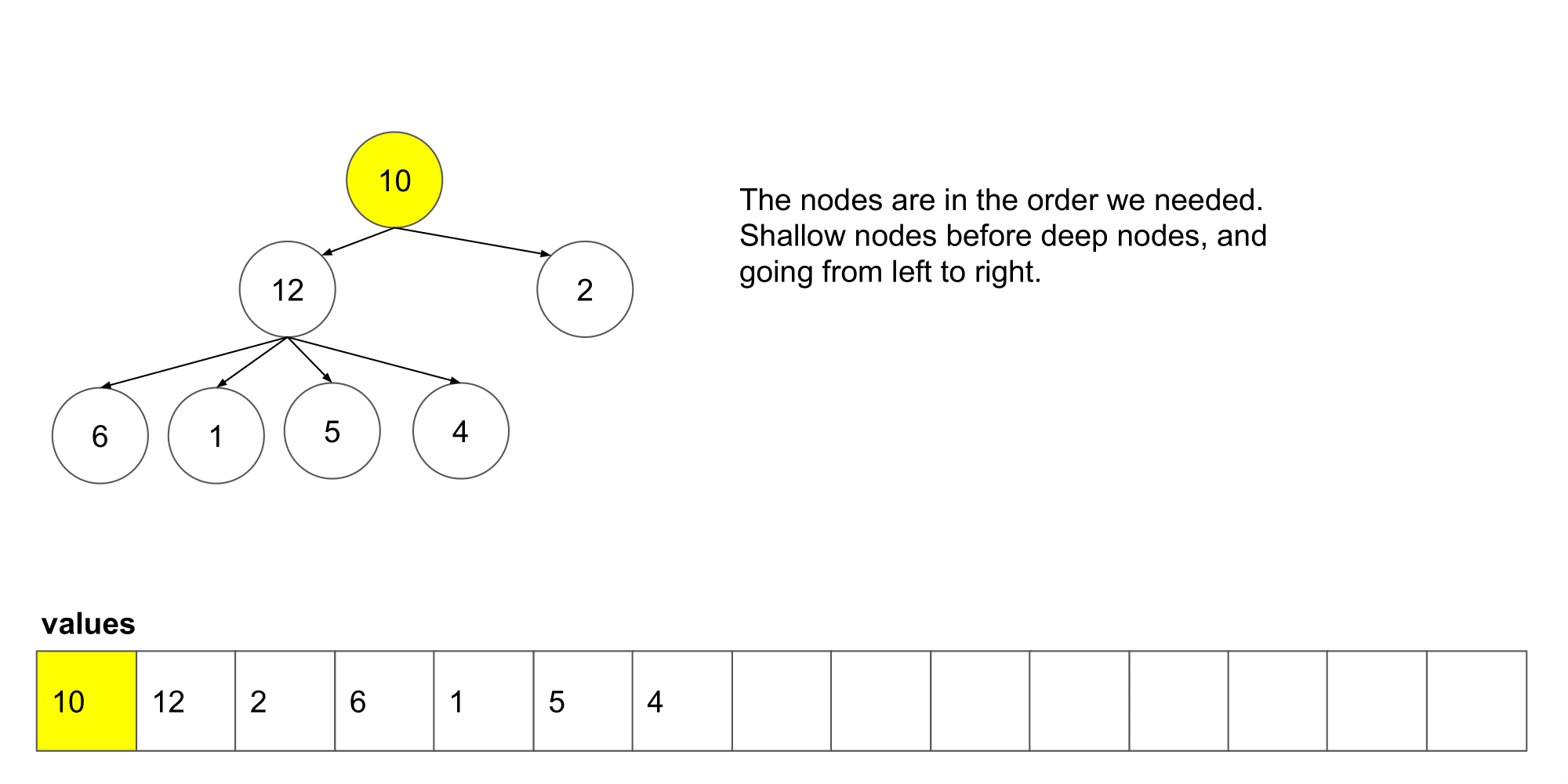
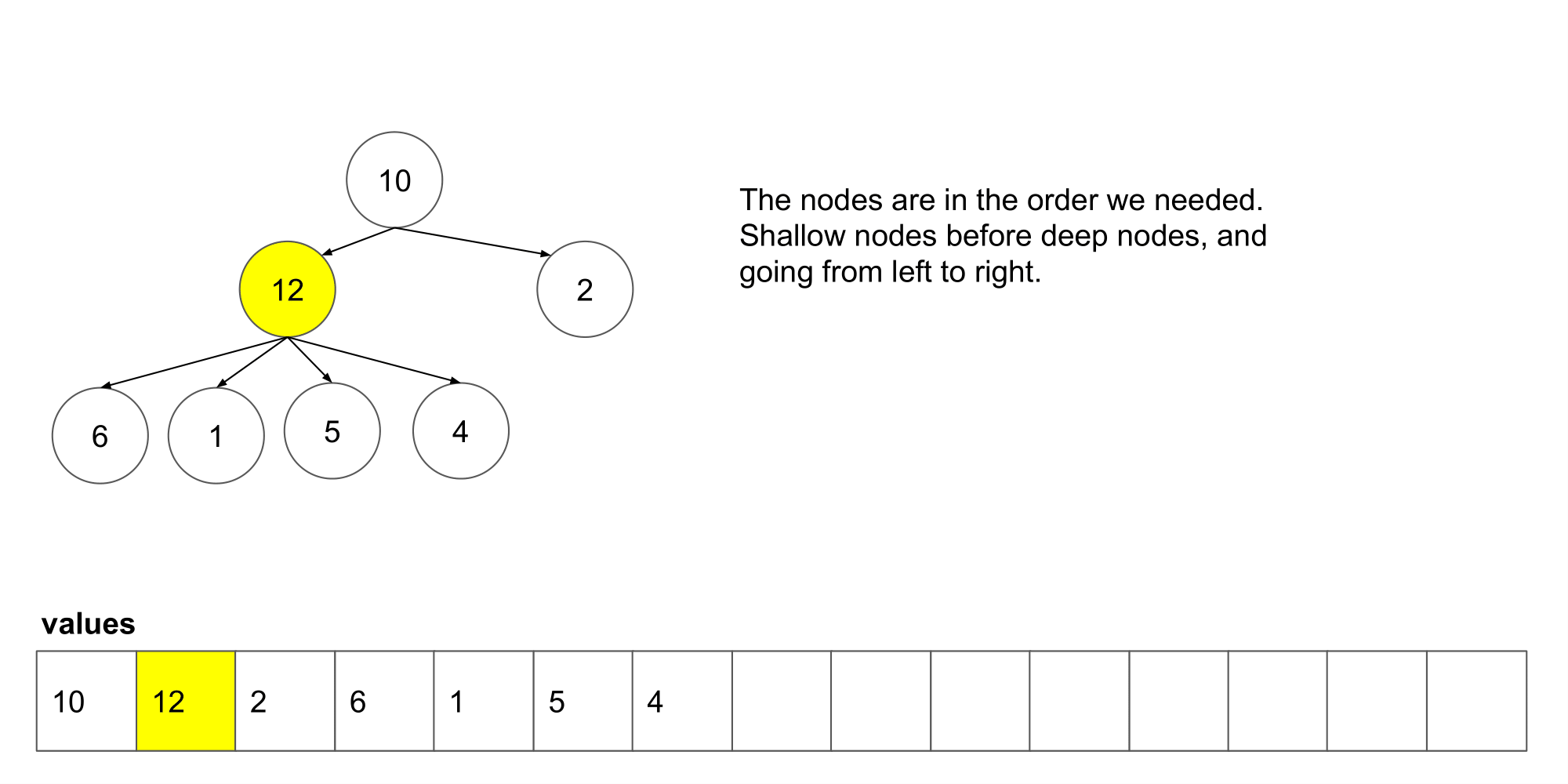
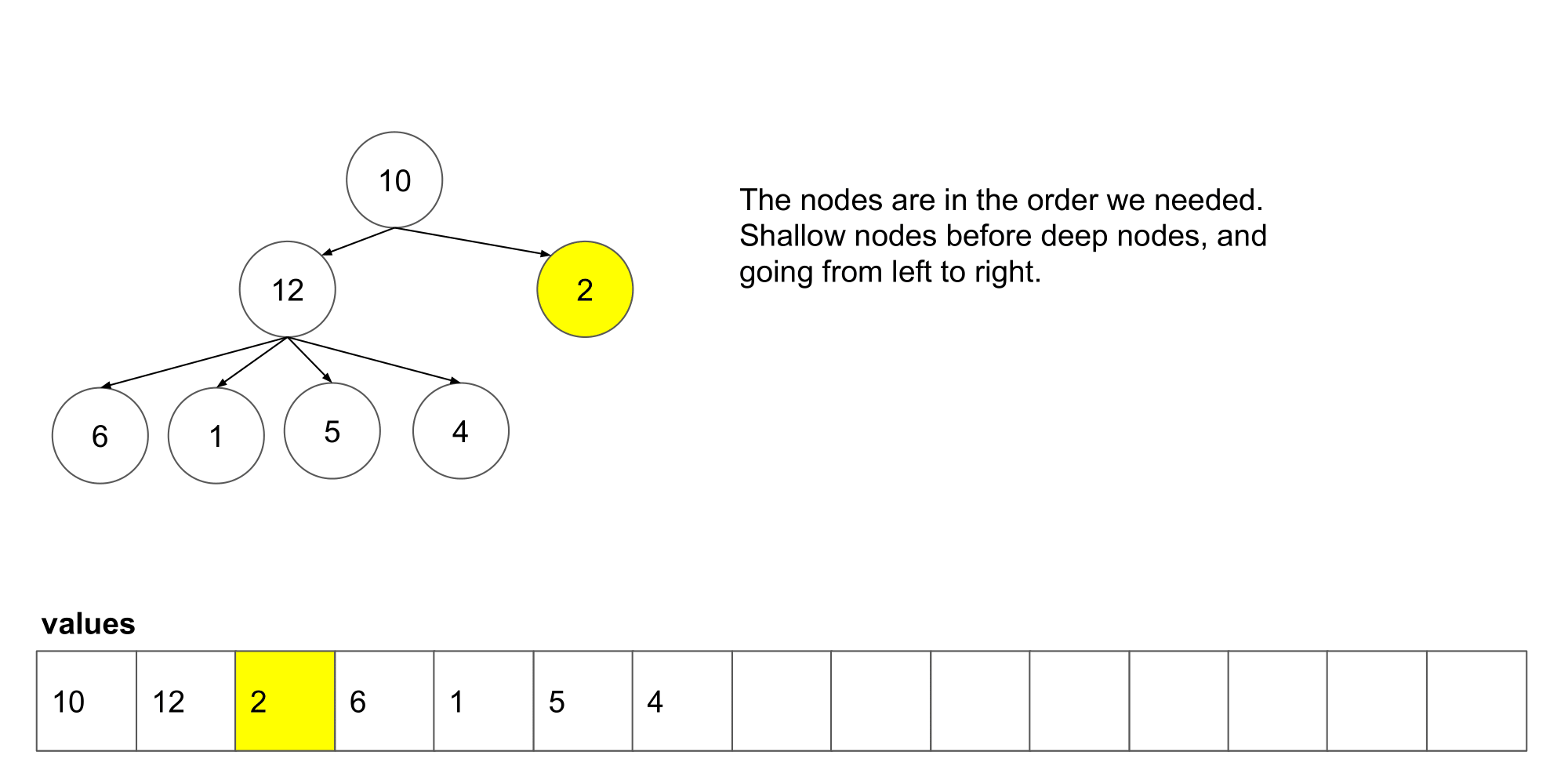
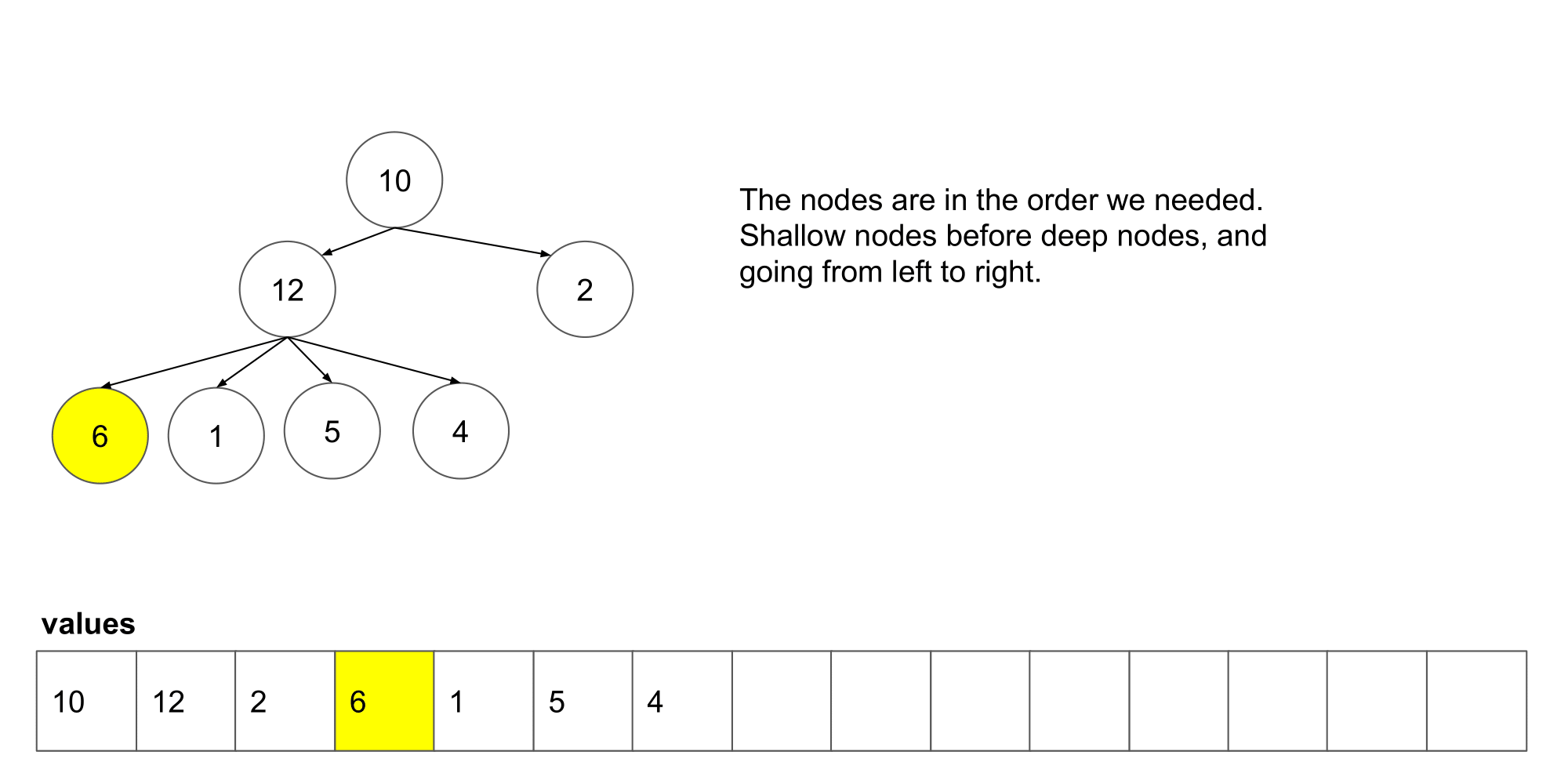
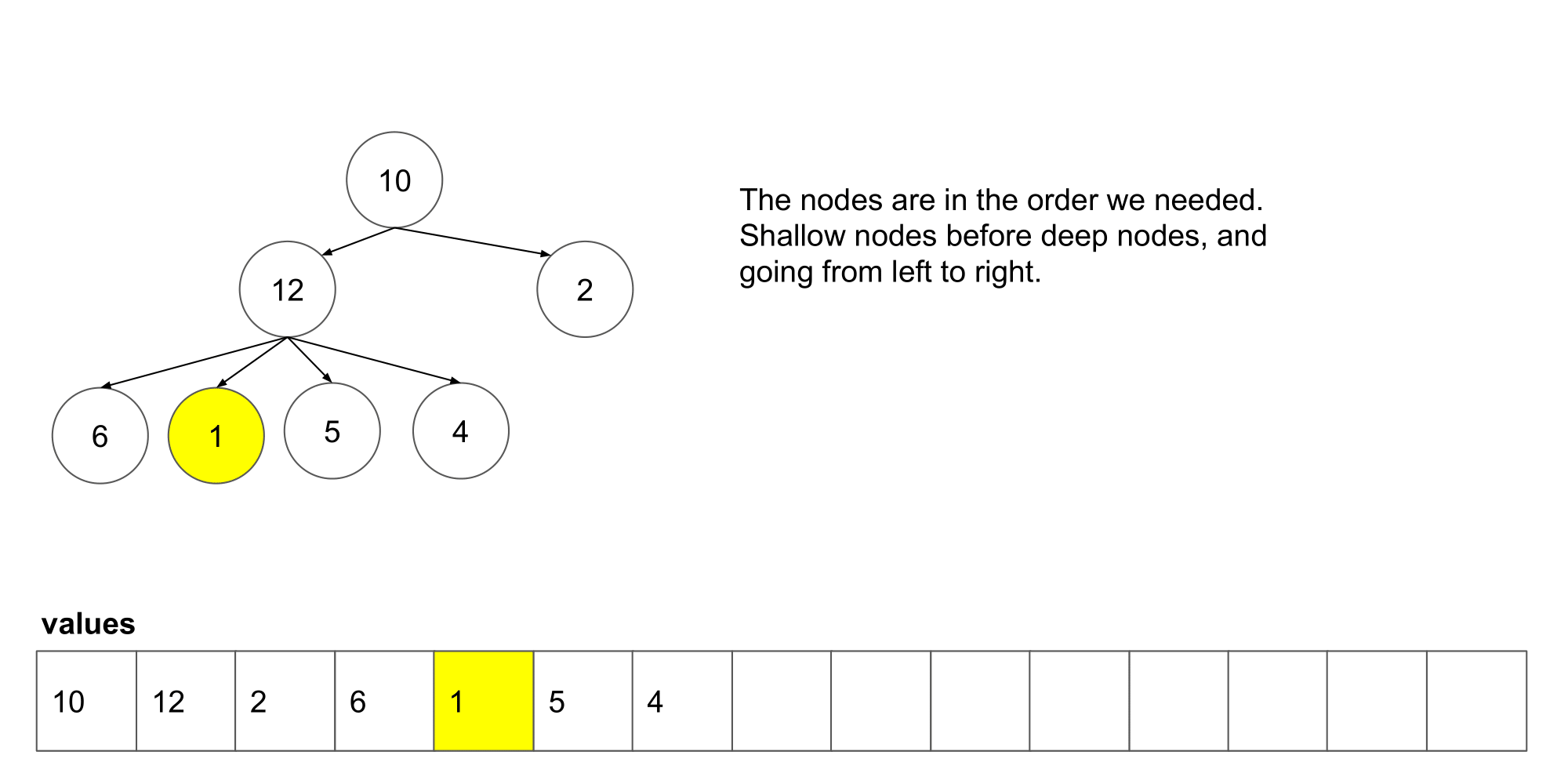
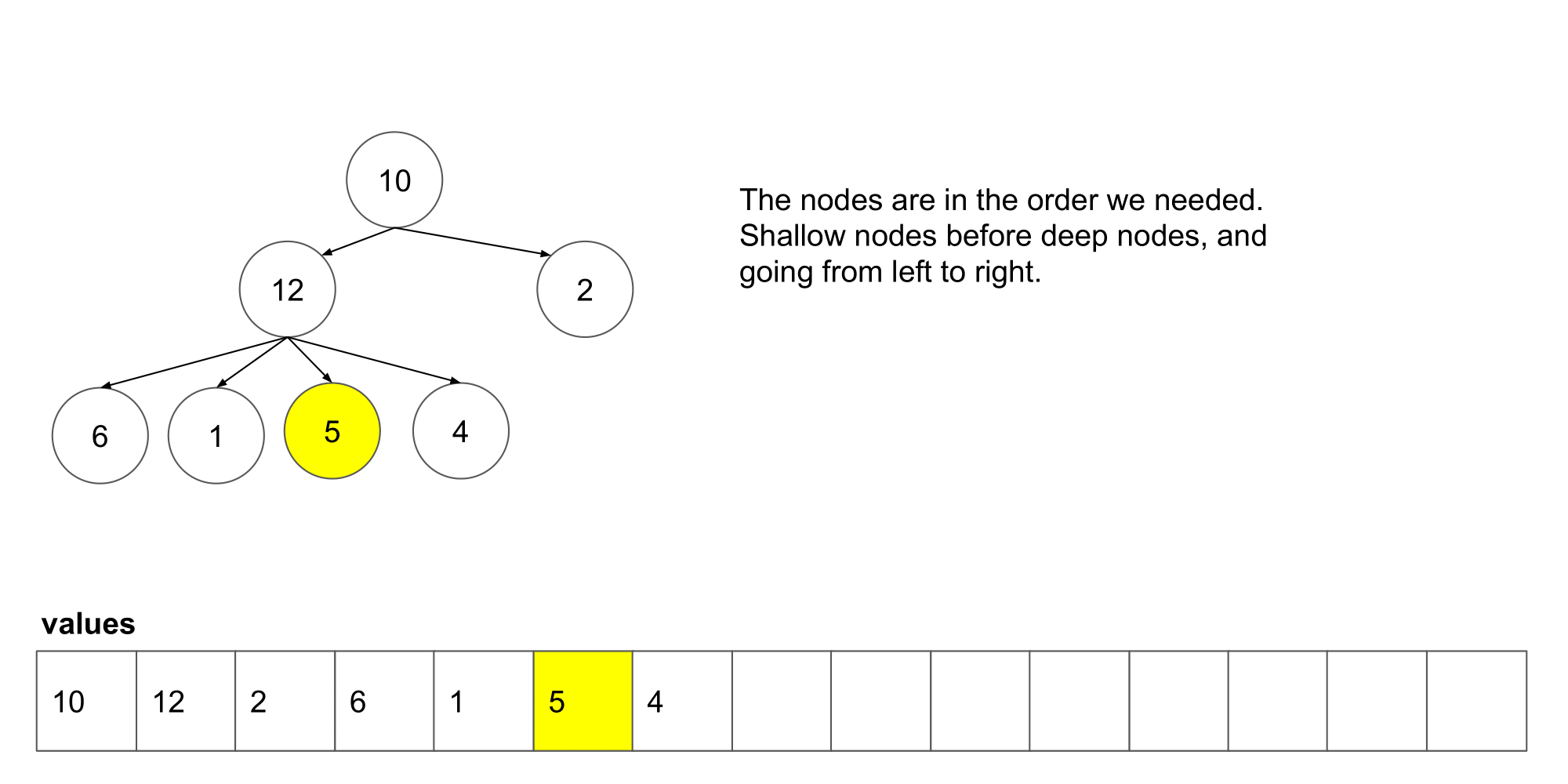
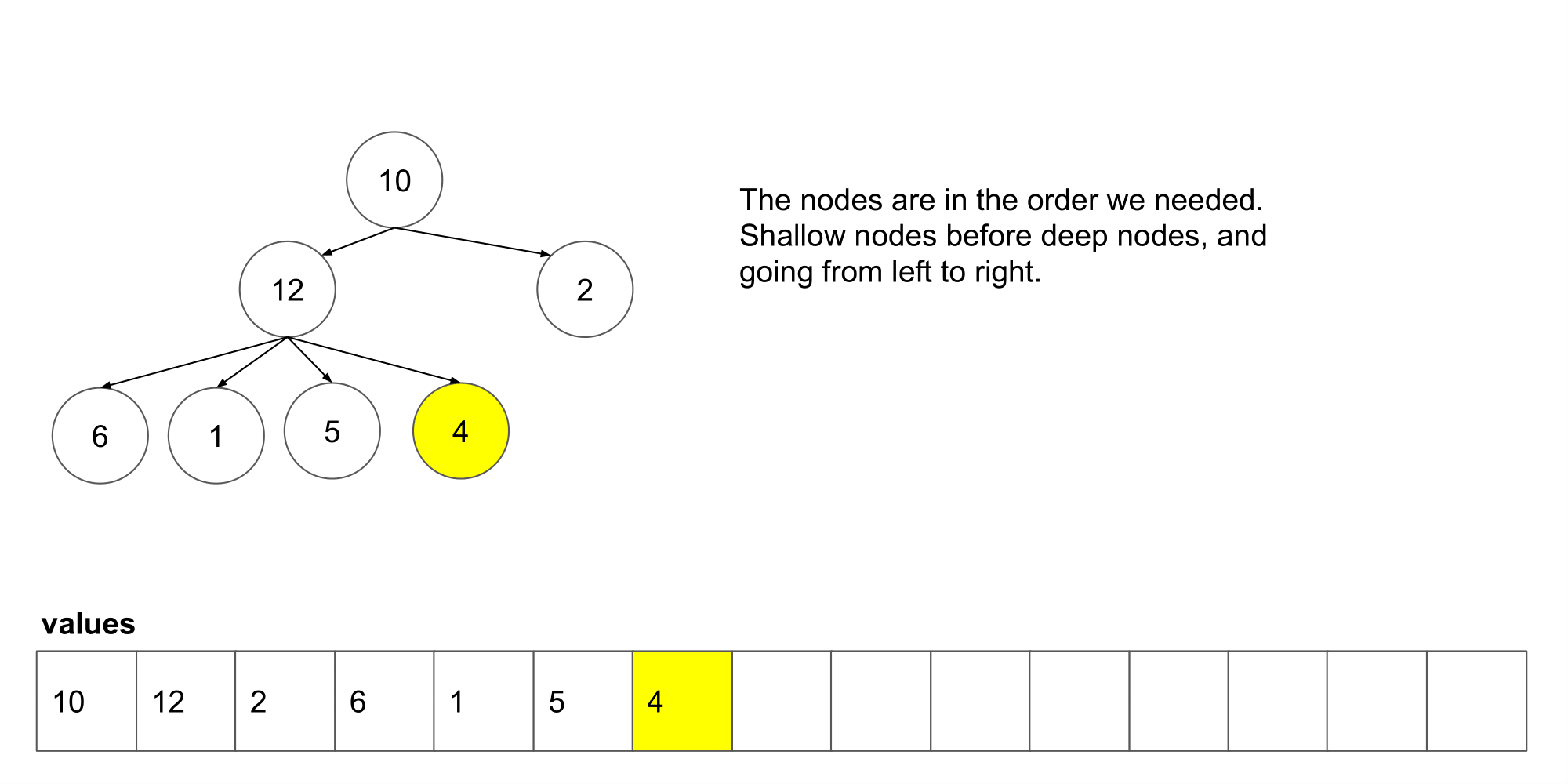
我们可以看到它从左到右，并且从上到写顺序遍历节点。下一步，我们将研究如何如何在这个算法的基础上保存每一层的列表。

算法：

上面的基本算法在一定程度上帮助了我们解决这道题目，但是我们还需要保存每一层的列表，并且在根节点为空时正常工作。

再构造下一层的列表时，我们需要创建新的子列表，然后将该层的所有节点的值插入到列表中。一个很好的方法时在 while 循环体开始时记录队列的当前大小 size。然后用另一个循环来处理 size 数量的节点。这样可以保证 while 循环在每一次迭代处理一层。

使用队列十分重要，如果使用 Vector，List，Array 的话，我们删除元素需要 O(n)O(n) 的时间复杂度。而队列删除元素只需要 O(1)O(1) 的时间。

// This code is a modified version of the code posted by

// #zzzliu on the discussion forums.

class Solution {

public List> levelOrder(Node root) {

List> result = new ArrayList<>();

if (root == null) return result;

Queue queue = new LinkedList<>();

queue.add(root);

while (!queue.isEmpty()) {

List level = new ArrayList<>();

int size = queue.size();

for (int i = 0; i < size; i++) {

Node node = queue.poll();

level.add(node.val);

queue.addAll(node.children);

}

result.add(level);

}

return result;

}

}

复杂度分析

时间复杂度：O(n)。n 指的是节点的数量。

空间复杂度：O(n).

方法二：简化的广度优先搜索

算法：

// This code is a modified version of the code posted by

// #zzzliu on the discussion forums.

class Solution {

public List> levelOrder(Node root) {

List> result = new ArrayList<>();

if (root == null) return result;

List previousLayer = Arrays.asList(root);

while (!previousLayer.isEmpty()) {

List currentLayer = new ArrayList<>();

List previousVals = new ArrayList<>();

for (Node node : previousLayer) {

previousVals.add(node.val);

currentLayer.addAll(node.children);

}

result.add(previousVals);

previousLayer = currentLayer;

}

return result;

}

}

复杂度分析

时间复杂度：O(n)。n 指的是节点的数量。

空间复杂度：O(n)，我们的列表包含所有节点。

方法三：递归

算法：

我们可以使用递归来解决这个问题，通常我们不能使用递归进行广度优先搜索。这是因为广度优先搜索基于队列，而递归运行时使用堆栈，适合深度优先搜索。但是在本题中，我们可以以不同的顺序添加到最终列表中，只要我们知道节点在哪一层并确保在那一层的列表顺序正确就可以了。

class Solution {

private List> result = new ArrayList<>();

public List> levelOrder(Node root) {

if (root != null) traverseNode(root, 0);

return result;

}

private void traverseNode(Node node, int level) {

if (result.size() <= level) {

result.add(new ArrayList<>());

}

result.get(level).add(node.val);

for (Node child : node.children) {

traverseNode(child, level + 1);

}

}

}

复杂度分析

时间复杂度：O(n)。n 指的是节点的数量

空间复杂度：正常情况O*(log*n)，最坏情况 O(n)。运行时在堆栈上的空间。