求四边形最大内接矩形,一种不规则多边形的最大内接矩形的快速近似求解方法与流程...

本发明属于几何数学的图像应用领域，可以应用于辅助图像预处理，具体涉及一种不规则多边形的最大内接矩形的快速近似求解方法，实现将图像处理后，比如说分割后的，不规则图像快速转换为神经网络，支持向量机等图像处理方法需要的矩形图像。

背景技术：

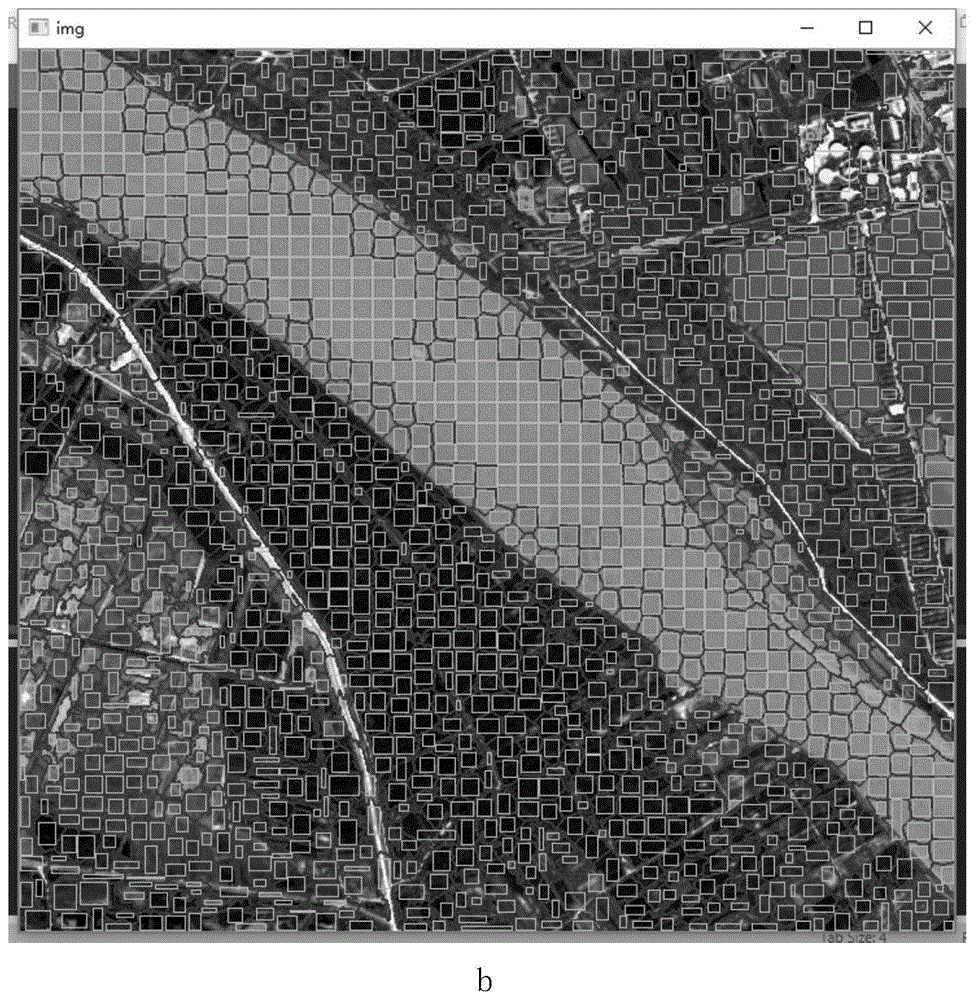
在图像解译中，我们主要会进行图像分割和图像分类两部分操作：首先，通过基于对象的分割生成一个个对象实体，例如遥感图像中的河流，山地等；随后，将分割出的实体传入分类器进行分类；然而，图片分类器大都需要输入图片为规则矩形，也就是欧几里得数据。在我们当前选用的能大幅提高精度的基于神经网络的分类器更是如此。而在现有技术中，主要有两种从非欧几里得数据转化到欧几里得数据的方法。

第一种是求取不规则多边形的最小外接矩形，这种方法优势在于能快速产生欧几里得数据，但是存在在外接矩形中却不在超像素的像素需要用镜像，均值等方法填充，这些填充方式生成的像素往往和真实像素大相径庭，从而大大降低了之后进行的分类的精度；第二种则是求取不规则多边形的最大内接矩形，内接矩形中的数据全部为真实数据，因此不会对分类器精度产生影响；然而传统生成最大内接矩形的方法，例如：中心扩散法等需要多次对矩形边界重新定位，降低了运算效率。

因此，如何高效高精度的求取分割图像内部不规则多边形的内接矩形用于神经网络的输入