判别分析分为r型和q型吗_浅谈聚类分析与判别分析

降维与分类是多元统计分析的两个主题，在这里，我浅谈一下的聚类分析和判别分析主要用于

分类。

聚类分析

按分析对象可分为两种：Q型聚类(对样本的聚类)，R型聚类(对变量的聚类)

按具体方法可分为两种：一般小样本数据可以用谱系聚类法，大样本数据一般用快速聚类法(K 均值聚类法)。

用谱系聚类法聚类时，聚多少类合适需要根据统计量判断，一般用R2统计量、半偏相关统计量、伪t2统计量以及伪F统计量。

这里给出谱系聚类法算法：

1)n个样品开始时作为n个类，计算两两之间的距离，构成一个对称距离矩阵

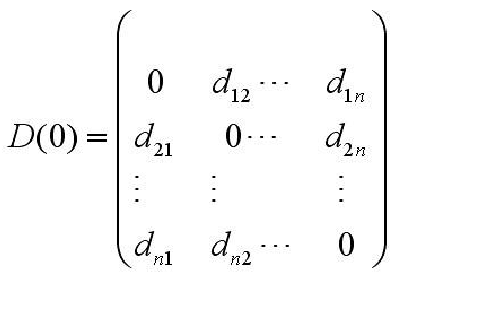
2)选择D(0)中的非对角线上的最小元素，设这个最小元素是D(pq)。这时G(p)={x(p)},G(q)={x(q)}。将G(p),G(q)合并成一个新类G(r)={G(p),G(q)}。在D(0)中消去G(p),G(q)所对应的行与列，并加入由新类G(r)与剩下的其他未聚合的类间的距离所组成的一行和一列，得到一个新的距离矩阵

D(1)，它是n-1阶方阵。

3)从D(1)出发重复步骤2的作法得D(2)。再由D(2)出发重复上述步骤，直到n个样品聚为1

个大类为止。

4)在合并过程中要记下合并样品的编号及两类合并时的水平(即距离)并绘制聚类谱系图。

判别分析

首先这里马氏距离的概念很重要，如下图。Σ是总体G的协方差矩阵，μ是总体G的均值向量

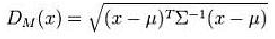
这构成了距离判别的核心。

其他主要几种判别法是Fisher判别，Bayes判别和逐步判别。一般用Fisher判别即可，要考虑概率及误判损失最小的用Bayes判别，但变量较多时，一般先进行逐步判别筛选出有统计意义的变量，再结合实际情况选择用哪种判别方法。

聚类分析与判别分析的区别与联系

都是研究分类的，在进行聚类分析前，对总体到底有几种类型不知道(研究分几类较为合适需从