初二下册计算机考试知识点,八年级初二下册数学期中考试知识点复习

欢迎阅读八年级下册数学期中考试知识点复习

第一章证明(二)

一. 等腰三角形

1. 性质：等边对等角

2. 判定：等角对等边

3. 推论：“三线合一”

4.等边三角形的性质及判定定理

例1、已知：如图1所示，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A 的度数为()

A．30°B．45°C．36°D．72°

图1

例2、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为()

A.30°

B.36°

C.45°

D.70°

已知等腰三角形一角，求其他两角的情况。

注意：等边三角形与轴对称、中心对称的关系。

二.直角三角形(含30°的直角三角形的边的性质)

※1. 勾股定理及其逆定理

※2. 命题与逆命题

※3. 直角三角形全等的判定定理

定理：斜边和一条直角边对应相等的两个直角三角形全等(HL)

三. 线段的垂直平分线

※1. 线段垂直平分线的性质及判定

※2.三角形三边的垂直平分线的性质

三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.

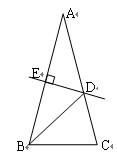
例1、如图，△ABC中，AB=AC，DE是AB的垂直平分线， AB=8，BC=4，∠A=36°，则∠DBC= ， = ．

△BDC的周长C

四. 角平分线