浮点数是一种用于表示实数的数值表示形式,它使计算机能够处理非常大的或非常小的数值。例如,在科学计算中,我们经常需要处理像 6.022 × 10^23 这样的数字,使用浮点数表示可以极大地提高计算的灵活性和效率。

一、浮点数基础
浮点数允许计算机表示的范围远超整数,适用于处理科学、工程和财经等领域中的大范围数值。浮点数的形式化定义如下:
浮点数可以表示为:
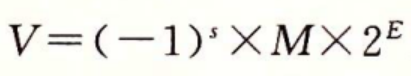
- sign:符号位,指示数值的正负
- mantissa(尾数或有效数字):具体的数字部分
- exponent(指数):控制数值范围的指数部分
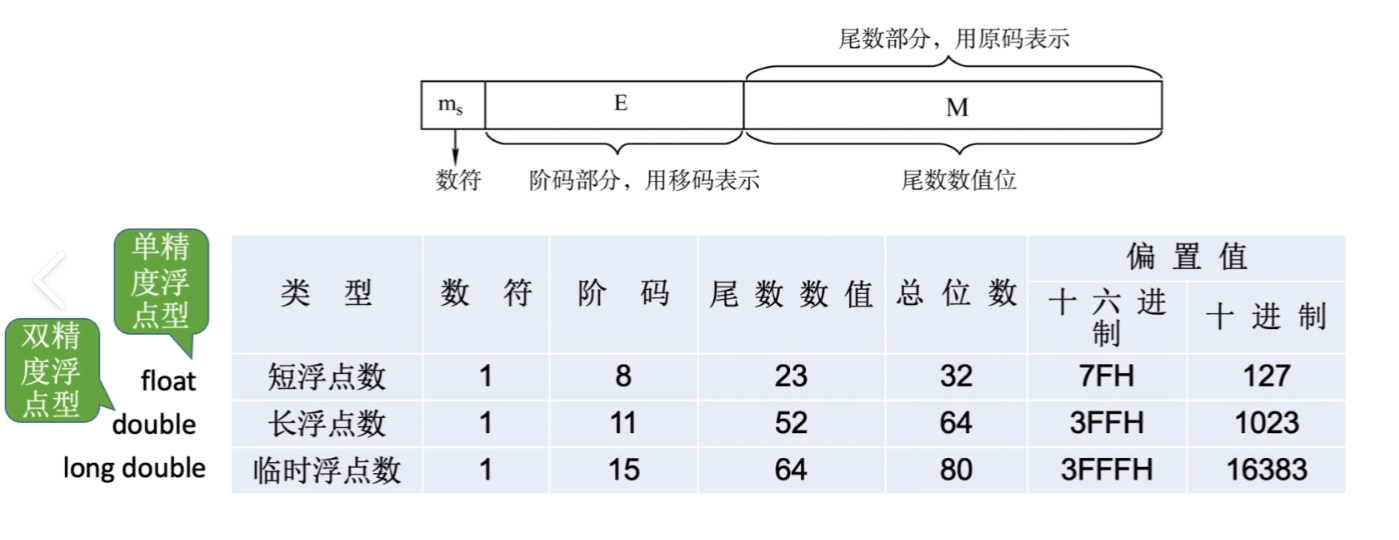
1.浮点数表示
例如,我们想表示数值 -6.75,可以将其分解为:
- 符号位 (sign):由于值为负,所以符号位为 1。
- 尾数 (mantissa):
6.75可以表示为二进制110.11,规范化为1.1011 × 2^2。 - 指数 (exponent):为了存储,须调整成偏移量表示。这里偏移量对于单精度为 127,因此指数为
2 + 127 = 129,其二进制表示为10000001。
最终,-6.75的单精度浮点数表示为:
2.浮点数的存储
在计算机内存中,浮点数以二进制方式存储:
- 单精度浮点数(32位):
- 1 bit 符号位
- 8 bits 指数
- 23 bits 尾数
- 双精度浮点数(64位):
- 1 bit 符号位
- 11 bits 指数
- 52 bits 尾数
因为尾数位数增加,双精度浮点数的表示范围和精度都要高于单精度浮点数。
二、IEEE 754标准的细节
1.数据格式
IEEE 754支持不同的浮点格式,包括但不限于:
- 单精度 (32 位)
- 符号位 (1位)
- 指数 (8位)
- 尾数 (23位)
- 双精度 (64 位)
- 符号位 (1位)
- 指数 (11位)
- 尾数 (52位)
- 扩展精度,例如 80 位用于某些硬件架构(如 x86 架构)。
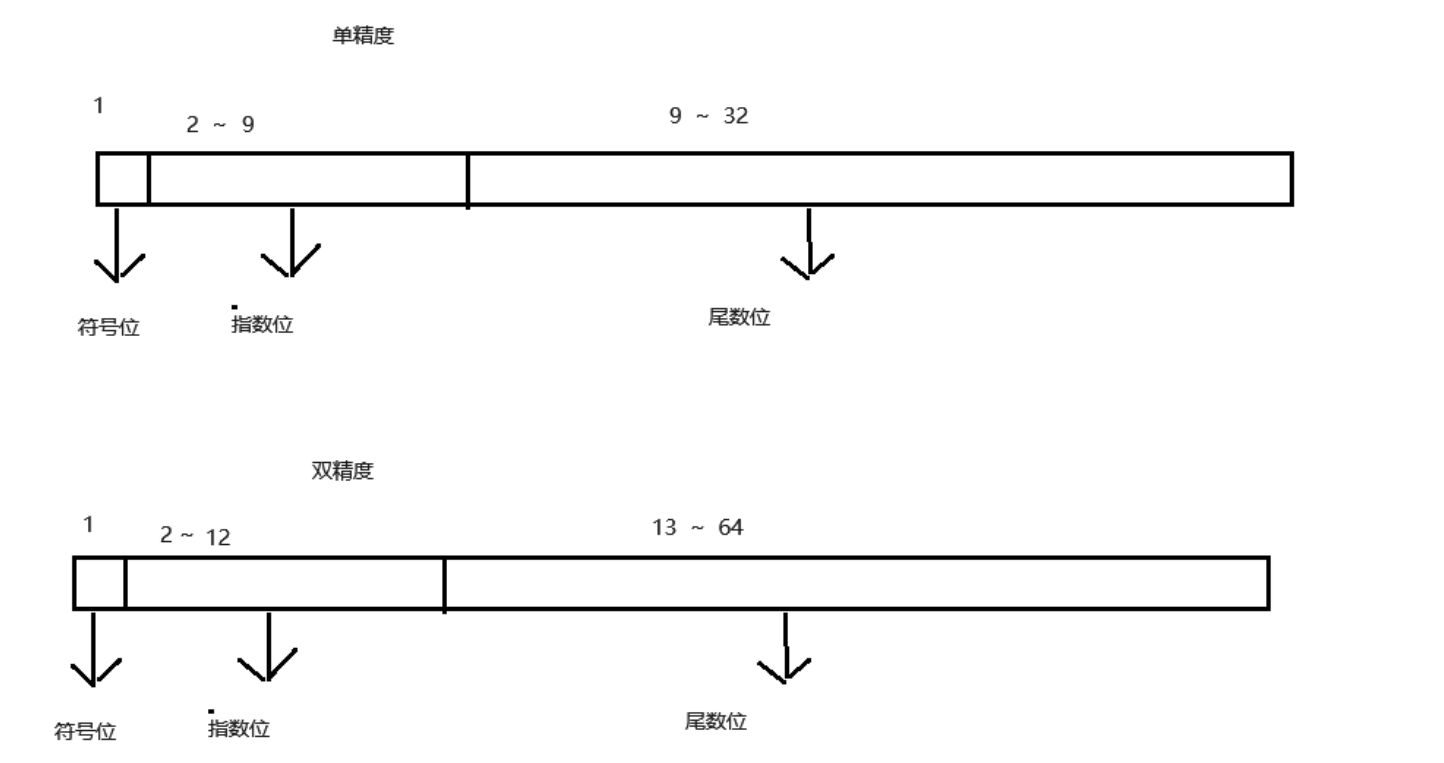
2.指数表示
IEEE 754采用偏移量表示法来存储指数值。这意味着实际二进制指数值需要加上一个常数(偏移量),以便能表示负值。例如:
- 单精度指数的偏移量为 127。因此,实际指数加上 127,得到偏移后的值进行存储。
- 双精度指数的偏移量为 1023。
这种方法使得可以用无符号整型存储负数的指数。
3.IEEE 754规格化
步骤 1: 确定符号位
- 符号位(Sign bit, S)决定浮点数是正数还是负数。如果数为正,则符号位为 0;如果为负,则符号位为 1。
步骤 2: 将十进制数转换为二进制数
- 将整个十进制数部分转换为二进制。如果存在小数部分,可以采用以下两种方法:
- 整数部分:通过不断除以 2,记录每次的余数,直到结果为 0,然后反向排列得到二进制数。
- 小数部分:通过不断乘以 2,记录每次的整数部分(0 或 1),直到达到所需的精度或达到预定的迭代次数。
步骤 3: 规范化二进制数
- 所得的二进制数需要进行规范化:
- 将二进制数表示为 (1.x \times 2^E) 的形式,其中 1 是隐含的(即不需要写出来),x 是小数部分。
例如:
- 二进制数:
1010.101规范化为1.010101 × 2^3,指数 E = 3。
步骤 4: 计算偏移量并确定指数
- 根据选择的浮点格式,确定偏移量。对于:
- 单精度(32位):偏移量为 127。
- 双精度(64位):偏移量为 1023。
- 将规范化后的指数 (E) 加上偏移量,计算出最终的存储指数 (E_{biased})。
例如:
- 如果 (E = 3)(单精度),则 (E_{biased} = 3 + 127 = 130)。
步骤 5: 生成指数位
- 将 (E_{biased}) 转换为二进制,得到相应的指数位。
- 对于单精度浮点数,使用 8 位来存储指数位;对于双精度浮点数,使用 11 位。
例如:
- (130) 的二进制为
10000010(对于单精度)。
步骤 6: 生成尾数(有效数字)
- 尾数是规范化后1.x 部分的小数部分。将其转换为二进制并填充到规定的位数:
- 单精度:后面有 23 位。
- 双精度:后面有 52 位。
- 尾数不包含隐含的 1。
例如:
- 对于
1.010101,尾数为010101,后面补 0 补齐到 23 位。
步骤 7: 组合成最终的 IEEE 754 表示
- 将符号位、指数位和尾数组合在一起,形成最终的 IEEE 754 位模式。
例如,对于一个负数 -10.625,转换为 IEEE 754 单精度的过程如下:
- 符号位 S = 1(负数)。
- 二进制表示:
-10.625=-1010.101。 - 规范化:
1.010101 × 2^3。 - 计算偏移量: (E_{biased} = 3 + 127 = 130)。
- 指数位:
10000010。 - 尾数:
01010100000000000000000。 - 最终组合:
1 10000010 01010100000000000000000。
4.舍入模式
在浮点数运算中,舍入至关重要,因为任何非精确的小数都需要处理。IEEE 754标准定义了多个舍入模式:
- 向最接近的偶数舍入(默认):例如,0.5会向下舍入,2.5将向下转换为2。
- 向零舍入(截断):总是舍去小数部分,不论其大小。
- 向上舍入:总是向上舍入,保留绝对值更大的数。
- 向下舍入:总是向小数部分更小的数舍去。
1)向最近偶数舍入(Round to Nearest, Even)
这一模式是IEEE 754的默认舍入方式。它会将结果舍入到最接近的可表示的数值。如果结果正好位于两个可表示数之间,则选择尾数为偶数的那个数。
示例
考虑将数字 2.5 舍入到最接近的单精度浮点数:
2.5在二进制中为10.1。它的最近可表示的浮点数是3.0 (11.0)和2.0 (10.0)。- 由于
2.5在两个数之间,最终结果应该舍入到2(即10.0)并保持尾数为偶数。
另一个例子:
3.5舍入为偶数的可表示数位受限于3.0和4.0(11.0和100.0),因此最终结果是4.0。
2)向零舍入(Round towards Zero)
这一模式始终舍弃小数部分,而只是简单地保留整数部分。这种方式计算结果每次都向零方向靠拢。
示例
- 对于
3.7,向零舍入将结果变为3.0。 - 对于
-3.7,结果则变为-3.0。
此模式不考虑后续的数字,因此有时可能导致小数部分的丢失。
3)向正无穷舍入(Round towards +∞)
这种模式总是向上舍入。无论是正数还是负数,都将结果“提升”到下一个可表示的数值。
示例
- 对于
3.2,向正无穷舍入结果为4.0。 - 对于
-3.2,在向正无穷舍入的过程中,会得到-3.0。
向正无穷舍入的特点是无论数值的符号如何,结果总是朝着绝对值较大的方向。
4)向负无穷舍入(Round towards -∞)
这种模式总是向下舍入。无论是正数还是负数,其结果总是“降低”到下一个可表示的数值。
示例
- 对于
3.7,向负无穷舍入结果为3.0。 - 对于
-3.7,结果则会舍入至-4.0。
这种舍入方式有助于处理一些需要保持保守估计的场合,尤其在金融领域比较常见。
这些不同的舍入模式确保在浮点运算中选择合适的方法处理结果,有助于减少误差。
5.异常处理
IEEE 754标准定义了浮点运算中的多种异常情况及其应对方式,包括:
- 溢出 (Overflow):当结果的绝对值超出所能表示的范围时,比如极大的数字相乘。
- 下溢 (Underflow):当结果太接近零而无法准确表示时,例如,极小的数字相乘。
- 无穷大 (Infinity):除以零的操作会产生无穷大,使程序能够检测到这些异界情况。
- 无效数 (NaN):例如,
0/0操作会产生一个“不是一个数字”的状态,帮助程序避免继续进行后续计算。

三、浮点数的局限性
尽管IEEE 754标准规范了浮点数的表示与运算,但仍存在显著的局限性:
1.精度限制
由于尾数位数有限,某些数值无法被精确表示。例如,十进制数 0.1 在二进制中是一个无限的循环小数。浮点计算经常会导致累积误差:
2.表示范围
IEEE 754浮点数能够表示的数值范围是有限的。单精度浮点数的最大值约为 3.4 × 10^38,处理更大范围数值时,必须使用双精度浮点数。溢出会导致错误,因此在开发软件时要谨慎。
3.性能开销
浮点运算通常比整数运算慢得多,还有额外的存储开销,尤其在资源有限的嵌入式系统中,这可能会造成性能瓶颈。





















 1086
1086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








