【时间序列】时间序列数据的预处理方法总结

【时间序列】时间序列数据的预处理方法总结

时间序列数据随处可见，要进行时间序列分析，我们必须先对数据进行预处理。时间序列预处理技术对数据建模的准确性有重大影响。

在本文中，我们将主要讨论以下几点：

• 时间序列数据的定义及其重要性。

• 时间序列数据的预处理步骤。

• 构建时间序列数据，查找缺失值，对特征进行去噪，并查找数据集中存在的异常值。

首先，让我们先了解时间序列的定义：

时间序列是在特定时间间隔内记录的一系列均匀分布的观测值。

时间序列的一个例子是黄金价格。在这种情况下，我们的观察是在固定时间间隔后一段时间内收集的黄金价格。时间单位可以是分钟、小时、天、年等。但是任何两个连续样本之间的时间差是相同的。

在本文中，我们将看到在深入研究数据建模部分之前应执行的常见时间序列预处理步骤和与时间序列数据相关的常见问题。

时间序列数据预处理

时间序列数据包含大量信息，但通常是不可见的。与时间序列相关的常见问题是无序时间戳、缺失值（或时间戳）、异常值和数据中的噪声。在所有提到的问题中，处理缺失值是最困难的一个，因为传统的插补（一种通过替换缺失值来保留大部分信息来处理缺失数据的技术）方法在处理时间序列数据时不适用。为了分析这个预处理的实时分析，我们将使用 Kaggle 的 Air Passenger 数据集。

时间序列数据通常以非结构化格式存在，即时间戳可能混合在一起并且没有正确排序。另外在大多数情况下，日期时间列具有默认的字符串数据类型，在对其应用任何操作之前，必须先将数据时间列转换为日期时间数据类型。让我们将其实现到我们的数据集中：

import pandas as pd 
 
passenger = pd.read_csv('AirPassengers.csv') 
passenger['Date'] = pd.to_datetime(passenger['Date'])  
passenger.sort_values(by=['Date'], inplace=True, ascending=True)

时间序列中的缺失值

处理时间序列数据中的缺失值是一项具有挑战性的任务。传统的插补技术不适用于时间序列数据，因为接收值的顺序很重要。为了解决这个问题，我们有以下插值方法：

插值是一种常用的时间序列缺失值插补技术。它有助于使用周围的两个已知数据点估计丢失的数据点。这种方法简单且最直观。处理时序数据时可以使用以下的方法：

• 基于时间的插值

• 样条插值

• 线性插值

让我们看看我们的数据在插补之前的样子：

from matplotlib.pyplot import figure 
import matplotlib.pyplot as plt 
 
figure(figsize=(12, 5), dpi=80, linewidth=10) 
plt.plot(passenger['Date'], passenger['Passengers']) 
plt.title('Air Passengers Raw Data with Missing Values') 
plt.xlabel('Years', fontsize=14) 
plt.ylabel('Number of Passengers', fontsize=14) 
plt.show()

让我们看看以上三个方法的结果：

passenger[‘Linear’] = passenger[‘Passengers’].interpolate(method=’linear’) 
passenger[‘Spline order 3’] = passenger[‘Passengers’].interpolate(method=’spline’, order=3) 
passenger[‘Time’] = passenger[‘Passengers’].interpolate(method=’time’) 
 
methods = ['Linear', 'Spline order 3', 'Time'] 
 
from matplotlib.pyplot import figure 
import matplotlib.pyplot as plt 
for method in methods: 
    figure(figsize=(12, 4), dpi=80, linewidth=10) 
    plt.plot(passenger["Date"], passenger[method]) 
    plt.title('Air Passengers Imputation using: ' + types) 
    plt.xlabel("Years", fontsize=14) 
    plt.ylabel("Number of Passengers", fontsize=14) 
    plt.show()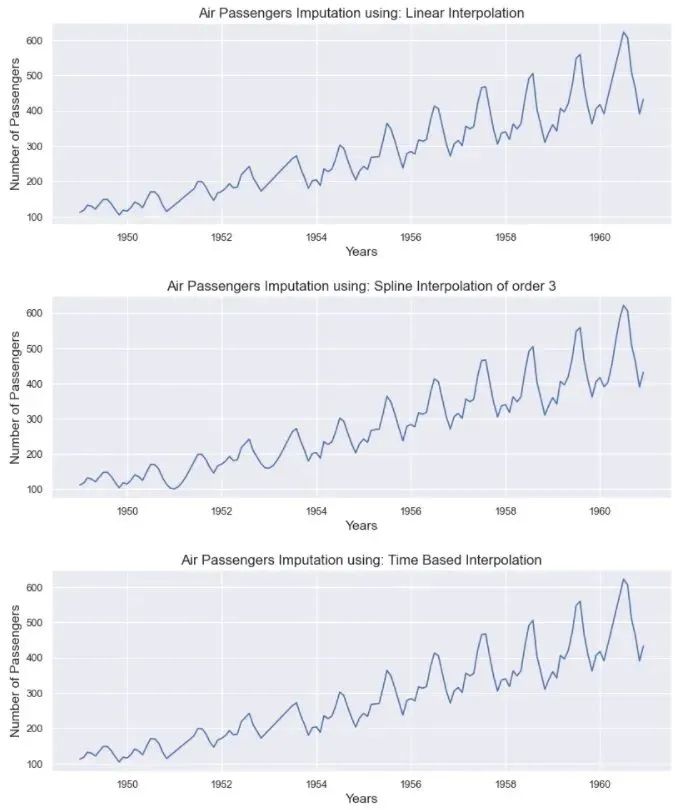

所有的方法都给出了还不错的结果。当缺失值窗口(缺失数据的宽度)很小时，这些方法更有意义。但是如果丢失了几个连续的值，这些方法就更难估计它们。

时间序列去噪

时间序列中的噪声元素可能会导致严重问题，所以一般情况下在构建任何模型之前都会有去除噪声的操作。最小化噪声的过程称为去噪。以下是一些通常用于从时间序列中去除噪声的方法：

滚动平均值

滚动平均值是先前观察窗口的平均值，其中窗口是来自时间序列数据的一系列值。为每个有序窗口计算平均值。这可以极大地帮助最小化时间序列数据中的噪声。

让我们在谷歌股票价格上应用滚动平均值：

rolling_google = google_stock_price['Open'].rolling(20).mean() 
plt.plot(google_stock_price['Date'], google_stock_price['Open']) 
plt.plot(google_stock_price['Date'], rolling_google) 
plt.xlabel('Date') 
plt.ylabel('Stock Price') 
plt.legend(['Open','Rolling Mean']) 
plt.show()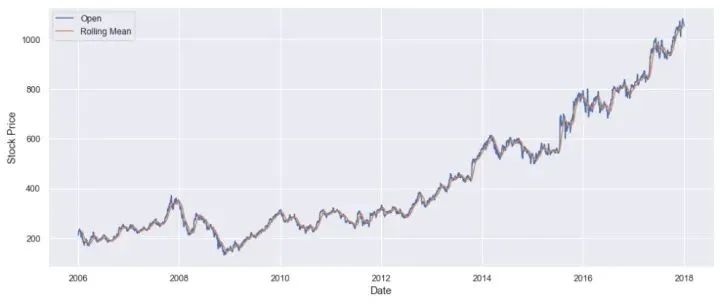

傅里叶变换

傅里叶变换可以通过将时间序列数据转换到频域来帮助去除噪声，我们可以过滤掉噪声频率。然后应用傅里叶反变换得到滤波后的时间序列。我们用傅里叶变换来计算谷歌股票价格。

denoised_google_stock_price = fft_denoiser(value, 0.001, True) 
plt.plot(time, google_stock['Open'][0:300]) 
plt.plot(time, denoised_google_stock_price) 
plt.xlabel('Date', fontsize = 13) 
plt.ylabel('Stock Price', fontsize = 13) 
plt.legend([‘Open’,’Denoised: 0.001']) 
plt.show()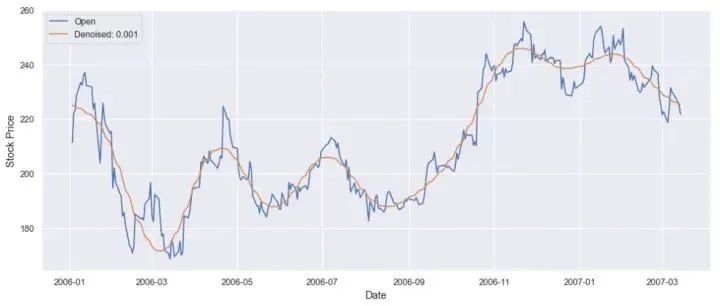

时间序列中的离群值检测

时间序列中的离群值是指趋势线的突然高峰或下降。导致离群值可能有多种因素。让我们看一下检测离群值的可用方法：

基于滚动统计的方法

这种方法最直观，适用于几乎所有类型的时间序列。在这种方法中，上限和下限是根据特定的统计量度创建的，例如均值和标准差、Z 和 T 分数以及分布的百分位数。例如，我们可以将上限和下限定义为：

取整个序列的均值和标准差是不可取的，因为在这种情况下，边界将是静态的。边界应该在滚动窗口的基础上创建，就像考虑一组连续的观察来创建边界，然后转移到另一个窗口。该方法是一种高效、简单的离群点检测方法。

孤立森林

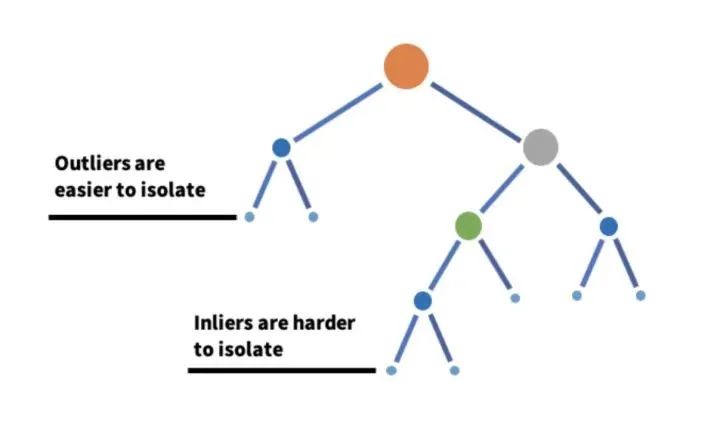
顾名思义，孤立森林是一种基于决策树的异常检测机器学习算法。它通过使用决策树的分区隔离给定特征集上的数据点来工作。换句话说，它从数据集中取出一个样本，并在该样本上构建树，直到每个点都被隔离。为了隔离数据点，通过选择该特征的最大值和最小值之间的分割来随机进行分区，直到每个点都被隔离。特征的随机分区将为异常数据点在树中创建更短的路径，从而将它们与其余数据区分开来。

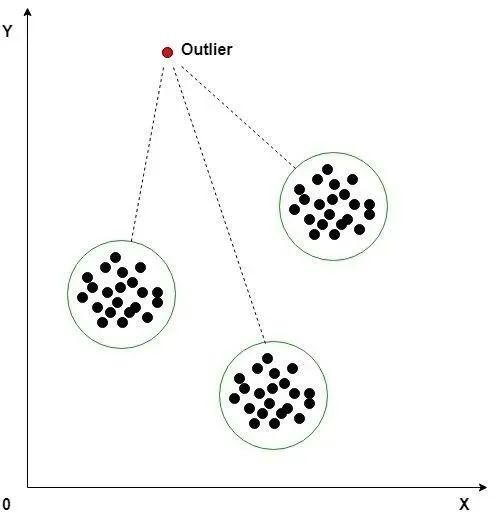
K-means 聚类

K-means 聚类是一种无监督机器学习算法，经常用于检测时间序列数据中的异常值。该算法查看数据集中的数据点，并将相似的数据点分组为 K 个聚类。通过测量数据点到其最近质心的距离来区分异常。如果距离大于某个阈值，则将该数据点标记为异常。K-Means 算法使用欧几里得距离进行比较。

可能的面试问题

如果一个人在简历中写了一个关于时间序列的项目，那么面试官可以从这个主题中提出这些可能的问题：

• 预处理时间序列数据的方法有哪些，与标准插补方法有何不同？

• 时间序列窗口是什么意思？

• 你听说过孤立森林吗？如果是，那么你能解释一下它是如何工作的吗？

• 什么是傅立叶变换，我们为什么需要它？

• 填充时间序列数据中缺失值的不同方法是什么？

总结

在本文中，我们研究了一些常见的时间序列数据预处理技术。我们从排序时间序列观察开始；然后研究了各种缺失值插补技术。因为我们处理的是一组有序的观察结果，所以时间序列插补与传统插补技术不同。此外，还将一些噪声去除技术应用于谷歌股票价格数据集，最后讨论了一些时间序列的异常值检测方法。使用所有这些提到的预处理步骤可确保高质量数据，为构建复杂模型做好准备。

【时间序列】时间序列数据的预处理方法总结