神经网络与深度学习笔记（四）

第四章 神经网络可以计算任何函数的可视化证明

    神经网络的一个最显著的事实就是它可以计算任何的函数。不管这个函数是什么样，总会确保有一个神经网络能够对任何可能的输入$x$，其值$f(x)$（或者某个足够准确的近似）是网络的输出。即使这个函数有很多输入和输出，这个结果都是成立的。这个结果表明神经网络拥有一种普遍性。

4.1 两个预先声明

    第一点，不是说一个网络可以被用来准确地计算任何函数。而是说，我们可以获得尽可能好的一个近似。通过增加隐藏元的数量，我们可以提升近似的精度。
    第二点，近似的函数其实是连续函数。如果函数不是连续的，也就是有突变的跳跃，那么一般来说无法使用一个神经网络进行近似。
    总结，神经网络普遍性定理表述的是：包含一个隐藏层的神经网络可以用来按照任意给定的精度来近似任何连续函数。

4.2 一个输入和一个输出的普遍性

    首先构造神经网络，它能够近似一个只有一个输入和一个输出的函数。这是一个特例，但很容易扩展到有多个输入输出的函数上。
    从如下图的网络开始，它是一个只包含一个隐藏层的网络，有两个隐藏神经元，和单个输出神经元。

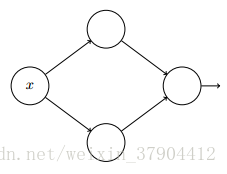
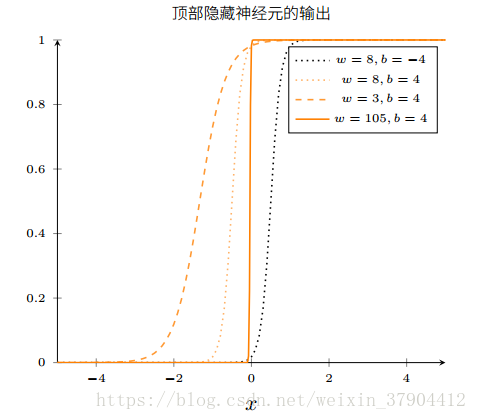
    考虑隐藏层的第一个神经元，其输出由$\sigma(wx+b)$决定。改变其参数$w$和$b$如下图，当$b$增加的时候，图形往左移动，但是形状不变；当$w$减小的时候，图形往两边拉宽了；当$w$增加的时候，图形变得越来越陡。当$w$超过100的时候，最终看上去就是阶跃函数。

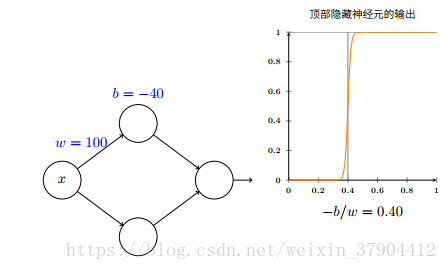
    发生阶跃的位置如何由权重和偏置确定呢？实际上，阶跃发生在$s=-\frac{b}{w}$的位置。

    使用参数$s$来简化描述隐藏神经元的方式：

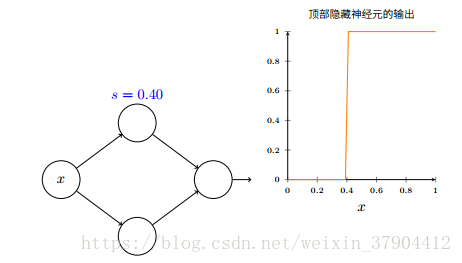
    我们只要设置输入上的权重$w$为一些大的值，然后令$b=-ws$，就能将一个以这种方式参数化的神经元换回常用的模型。
    再接着考虑整个网络的行为。下图右边展示的是加权输出的结果：$\sigma(w_1a_1+w_2a_2+b)$。调节参数可以观察到：
- 调节$s_1$和$s_2$的大小分别控制上下两个神经元的激活顺序。如果$s_1<s_2$，右图函数的第一个阶梯由第一个神经元输出决定，因为他先被激活。第二个阶梯才是两者的和。
- 调节$w_1$和$w_2$分别控制两个神经元输出在输出神经元的权重，当其中一个为0时，只剩下一个输入，右边的函数也显示为只有一个阶跃函数。

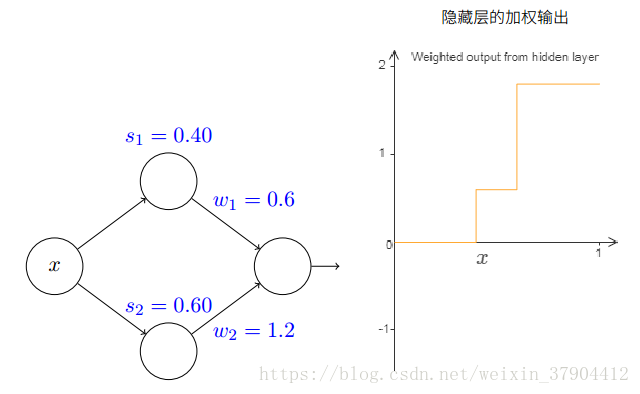
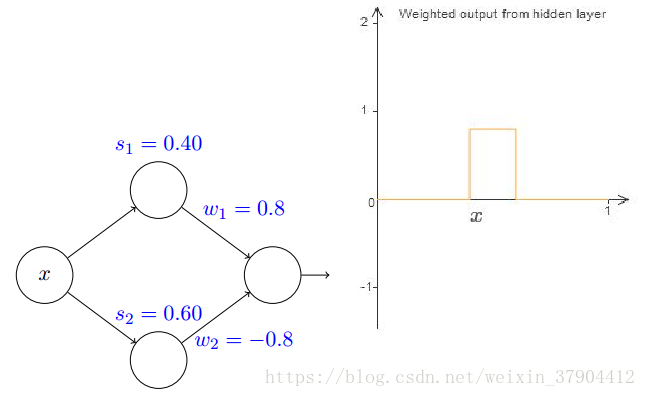
    最后，试着让$w1=0.8，w2=−0.8$，然后$s1=0.4，s2=0.6$就得到一个在$(0.4, 0.6)$上的门函数，它从$s_1$开始，到$s_2$结束，高为$0.8$：

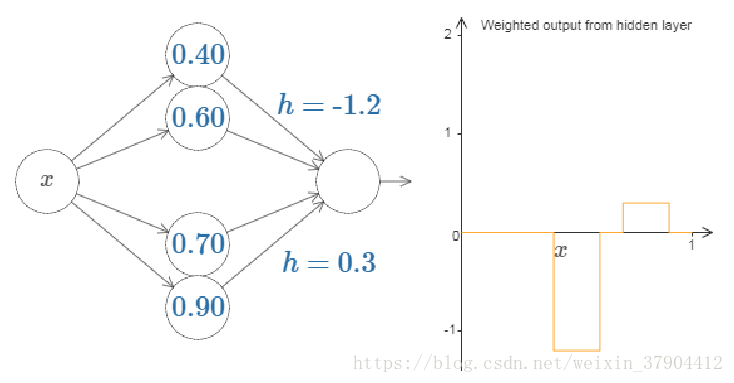
    如果我们固定$s_1$和$s_2$，然后$w_1=−w_2$，这样就可以将门函数看作是只有一个参数$h$的模型，其中$h=w_1$，对应着就是门函数的“门梁”的位置。通过组合神经元我们就可以轻易得到两个门函数组合的情况：

    同样的方法，我们可以构造任意数量任意高度的门函数。因为对于[0,1]这个区间的划分是可以有无限多N个，只要使用N对隐藏层神经元来设置任意期望高度的峰值，然后分别配上对应的$h$就可以达到要求了。

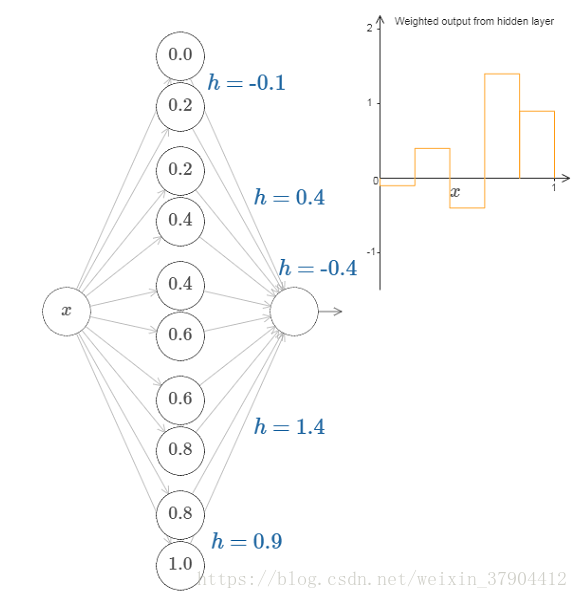
    上图就是一个五个宽度一样的门函数的情形，高度由各自的参数$h$决定。
    如果现在有一个任意函数$f(x)=0.2+0.4x^2+0.3xsin(15x)+0.05cos(50x)$，看看神经网络怎么去近似它。还是使用上述五个门函数的情形，通过调节各自的$h$得到近似要求的结果：


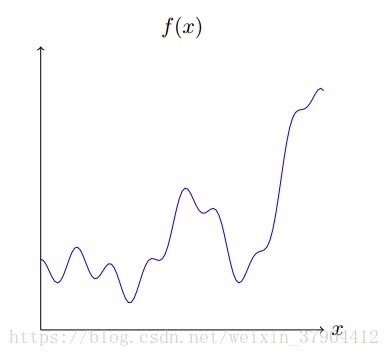
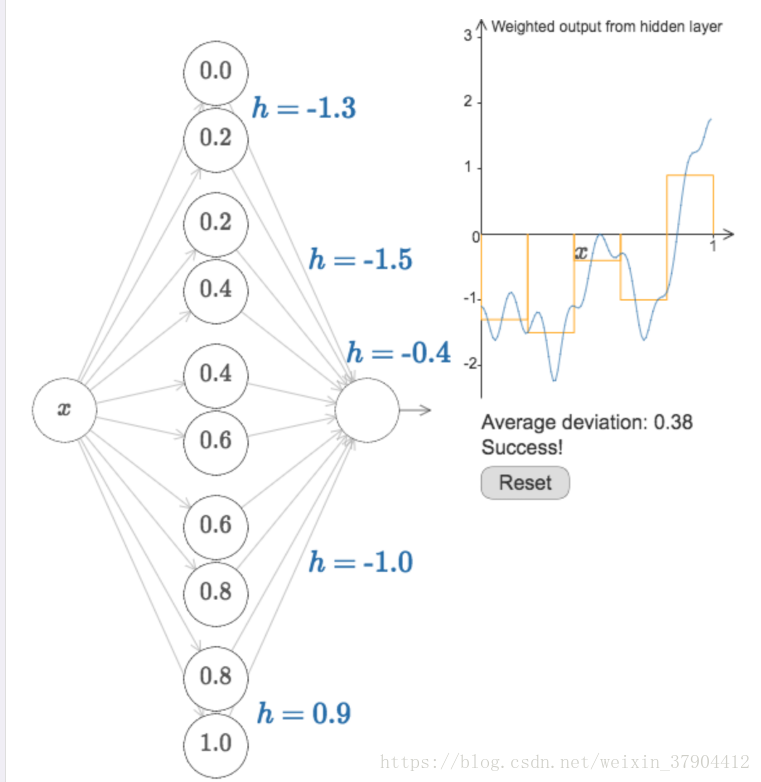
    这虽然只是一个粗略的近似，结果也不唯一，但是只要通过增加门函数的个数，即增加隐藏层神经元的个数，就可以让结果越来越精确。将这个得到的模型转换到我们的神经网络参数上，隐藏层的$w$取了很大的数$w=1000$，由于$s=-\frac{b}{w}=0.2$，得到$b=-1000*0.2=-200$。输出层的权重由$h$决定，例如第一个$h=-1.3$，说明他代表的两个权重$w_1=1.3，w_2=-1.3$。以此类推，这样就完成了通过构造一个神经网络来逼近目标函数的目的了，而且通过增加隐藏层神经元的个数（区间区分的越小）可以使得这个近似结果更加准确。

4.3 多个输入变量

    考虑一个神经元有两个输入的情况：

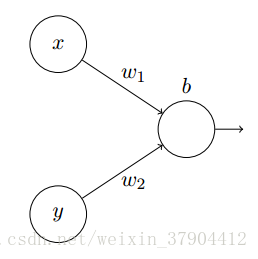
    将$x$和$y$看做变量，其加权输出和为因变量，这样就将之前的平面图像转变为三维图像。先设$w_2=0$，这样图像为：

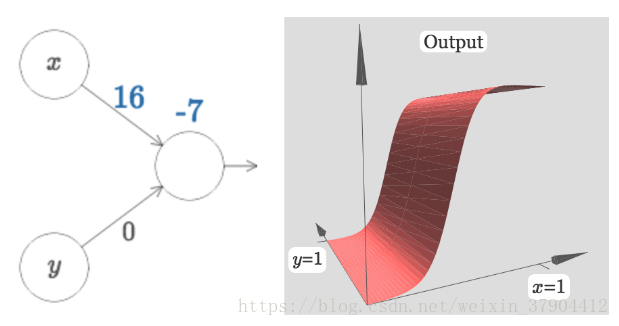
    随着输入权重变大，输出接近一个阶跃函数。可以改变偏置的位置来移动阶跃点的位置。阶跃点的实际位置是$s_x=-\frac{b}{w_1}$。以阶跃点位置作为参数绘制阶跃函数，图中的$x$表示阶跃方向在x轴方向。

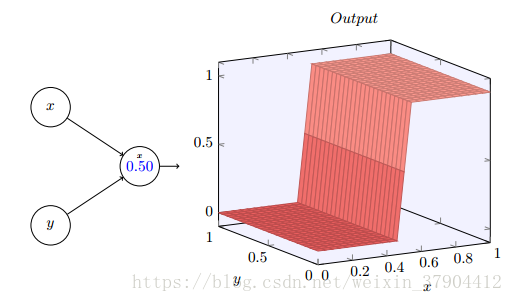
    如果设$w_1=0$，就可以得到一个$y$轴方向的阶跃函数。

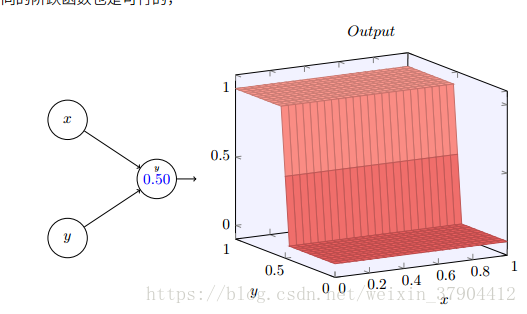
    接着通过组合，可以得到对应门函数的三维情况。

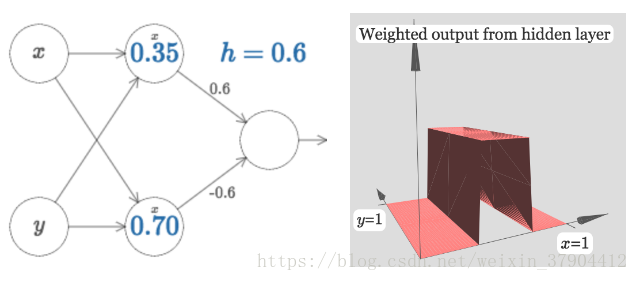
    注意这里的$y$并没有起到作用，和$y$相连的权重都被设置成了0。类似也有只有$y$的版本，将和$x$的相连的权重设置为0：

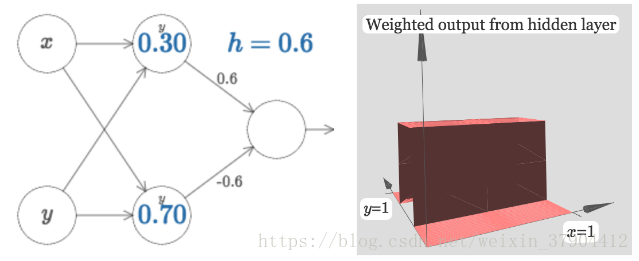
    如果我们将这两个方向垂直的门函数相加：

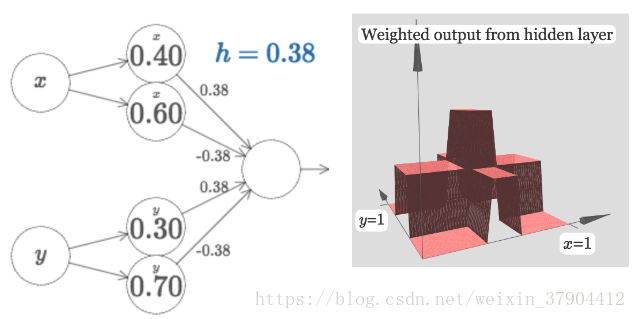
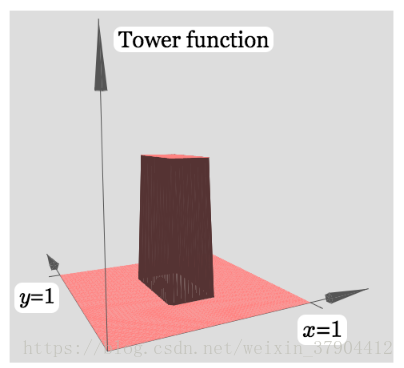
    改变$h$的大小可以改变图像的高度，很容易可以知道中间最高的地方是边上的两倍高。我们于是想到能否用中间的高度作为中间区间上的值，这种方法去将定义域分割成一个个区间呢，然后每个区间对应一个值，区间分的越细就越逼近原函数。类似于之前单输入的情况。但是这就需要我们得到的是一个下图类似的塔函数：

    但是我们得到的情况是除了中间是高的（$2h$），边上并不是平的，也有一定的高度（$h$），并不满足塔函数的条件。怎么将其转变为塔函数的形状呢？如果我们选择适当的阈值（$h$和$b$），可以把高原下降到零，并且依然矗立着塔。下图，选择$h=10，b\approx-\frac{3h}{2}$

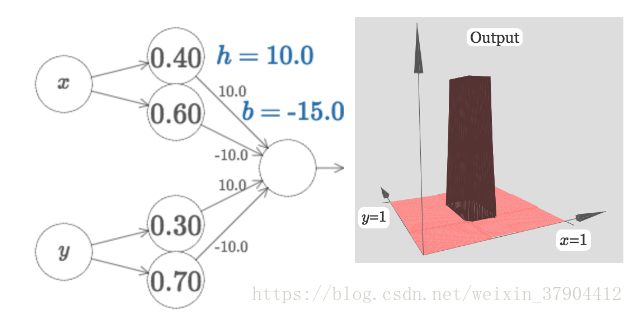
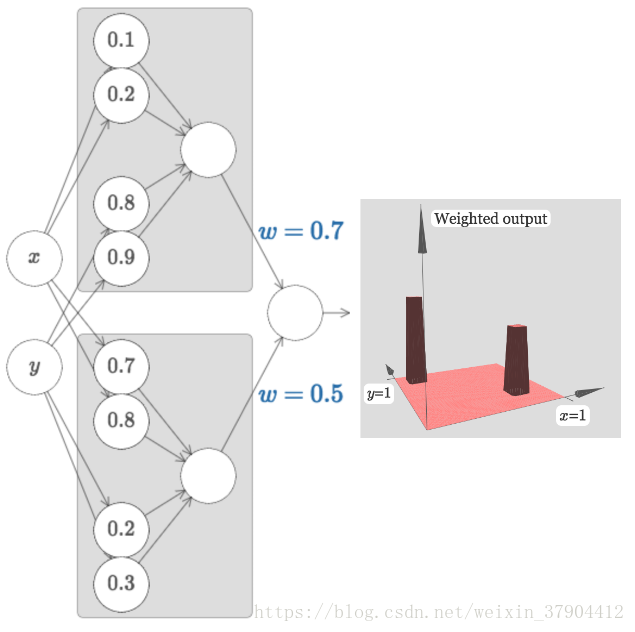
    一个塔对应着一个隐藏层神经元的输出。将两个类似这样的神经网络组合可以得到两个塔函数，每个塔函数对应二维平面上的一个区域。以此类推，可以得到任意多个自定义高度的塔函数。

4.4 结论

    单层的神经网络就已经可以计算任何函数。但是，现实中的问题和知识体系往往是由浅入深的层级关系，而深度网络的层级结构就非常切合这一点。例如对于图像识别的问题，只是着眼于单个像素点的理解当然是不够的，我们更希望它能够识别出更复杂的模式：从简单的线条到复杂的几何形状等等。因此，在解决现实问题上，深度网络对于这种层级的问题处理结果的确要好于浅层网络。