3.4 Higher Order Consistencies

在3.3节中，我们已经看到，弧度一致性是收紧网络的最自然的技术，受到了社区的高度关注。 尽管如此，这并不是收紧网络的唯一方法，早在70年代，一些作者提出的技术发现了比弧度一致性更多的不一致性。

3.4.1 Path Consistency 

Montanari提出路径一致性是binary normalized网络中值对一致性的必要条件[95]。 粗略地说，如果对于一对变量（xi，xj）上的给定值对（vi，vj），存在从xi到xj的变量序列，这样我们就无法找到从vi到vj处完成这些变量的值序列，并且满足沿序列的所有二元约束，则（vi，vj）是不一致的。

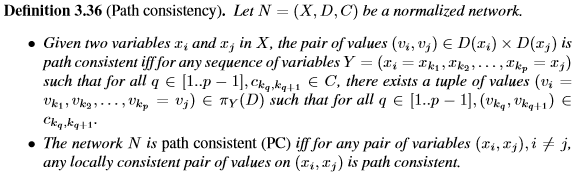
Montanari观察到仅在长度为2的路径上强制执行路径一致性以获得与路径一致性相同的本地一致性水平是足够的。

路径一致性不会减少变量域，但会删除值对。 结果，归一化网络N的路径一致性闭合不在Psol ND中。 我将PN2定义为PN的子集，其中网络被归一化，并且仅通过添加或收紧二进制约束使之与N不同。 N的路径一致闭包PC（N）是PN2中所有路径一致网络的并集（根据N）。在PN2中，可能存在几个与PC（N）nogood-等效的网络 —— 因为具有相同方案的约束可以在非有效元组上不同，这不会改变本地不一致的实例化的集合。 然而，PC算法可以扩展地表示修改约束，仅生成嵌入约束。 因此，如果我们考虑嵌入所有二进制约束的网络，则关系是PN2上的部分顺序，并且PC算法保证收敛于PC（N）。

文献中提出了几种实现PC的算法。 每次为弧一致性提出新技术时，它很快就会应用于路径一致性。 可以看出PC1 [95,87]是蛮力AC1的路径一致性计数器部分。 PC2是AC3对路径一致性的扩展[87]。 PC3 [92]和PC4 [68]使用支持列表，如AC4，以达到最佳性。 PC5 [111]和PC6 [32]扩展了AC6。 PC7 [31]和PC8 [33]是PC6的简化，在实践中表现良好。 PC5 ++ [111]应用AC7的双向性。 最后，PC2001 [126,25]扩展了AC2001。

路径一致性的一个缺点是强制执行它会产生CN中没有的其他约束（参见例3.37）。 此外，即使约束c（xi，x j）已经在CN中，PC的改进也可以强制改变其语义并且可以扩展地表示这个新约束，而它是作为函数给出的。

我们可以注意到的最后一点是，虽然通常在二进制规范化网络中考虑路径一致性，但定义3.36中没有任何内容阻止其在非二进制规范化网络上的使用。 非二进制约束只是被忽略了。

3.4.2 k-Consistencies

在Montanari的论文发表几年后，Freuder将局部一致性的概念从AC强化到了一整个类的一致性，称为k-一致性[53,54]。

k元一致性：对|Y|=k-1的变量集，第k个变量能找到至少一个值，使它和变量集中的其他变量共同组成一个解。

3-consistency和(2-)path consistency是不等价的。正如Dechter [46]所观察到的，即使3-consistency与（2-）路径一致性具有很强的相似性，它也不是等价的。 实际上，3-一致性确保长度为2的任何实例化都可以扩展到涉及任何第三变量的实例化而不违反任何约束，而（2-）路径一致性仅保证不违反二进制约束。

k-consistency确保每次我们有一个大小为k-1的本地一致的实例化时，我们可以始终将它扩展到任何第k个变量。 那么，问题是“如何构建大小为k-1的本地一致实例化？”。 强k-一致性是保证网络在1≤j≤k时j-一致的性质。 因此，我们可以从头开始构建一个大小为k的本地一致的实例，而不需要任何回溯。

Freuderand Cooper在[53,37]中提出的算法都达到了一个不是强k-一致闭包的点。 它们使所有约束（最多为arity k-1）尽可能明确。 例如，如果一对值（（xi，v i），（xj，v j））是路径不一致的，它们会在{xi，x j}的每个超集Y上创建一个约束，其中| Y | <k，并且该约束禁止在Y上的所有元组τ，其中τ[（xi，x j）] =（vi，v j）。 Cooper表明他的算法运行在中，这是强k-一致性的最佳时间复杂度。 Cooper提出的算法需要O（nkdk）空间。 强k-一致性的最佳空间复杂度是，因为我们必须存储k-consistency的每个约束k-1的约束，每次大小为k-1的实例化不延伸到第k个变量。

我在3.2节中说过，我们可以在网络上执行的最大简化量是达到一个全球一致的网络，也就是说，所有本地一致的实例都可以扩展到解决方案的网络。 强n-一致性保证了这一点。

在任意网络上实现全局一致性太耗费空间（在O（nn-1dn-1）中）。 Freuder给出了相关超图的条件，其中强k-一致性（k <n）足以允许无回溯搜索[54]。在[47]中，Dechter和Pearl开发了自适应一致性（AdC），这是一种受动态编程启发的技术。给定变量的总排序，AdC根据与xi共享约束的变量的数量以及在排序中在其之前的变量的数量来调整对每个变量xi强制执行的k-一致性的级别。获得的网络保证无回溯搜索。 （见第7章）在[55]中，Freuder提出了（i，j） - 一致性，k-一致性的推广，其中我们不保证大小为k-1的实例可以扩展到大小为k的实例，但是实例化大小我可以扩展到j个附加变量。 k-一致性是（k-1,1）一致性。由于k-一致性的主要缺点是它们需要存储大小为k-1的所有禁止实例的巨大空间，我们可以通过将i设置为（i，j） - 一致性中的小值来设计需要较少空间的局部一致性。

3.4.3 Montanari’s Decomposability and Minimality

3.4.3 Montanari的可分解性和极简性

蒙塔纳里描述了可以在多项式空间中全局一致的网络。 这些是一组解决方案是可分解关系的网络[95]，在[46]中也称为二进制可分解关系。

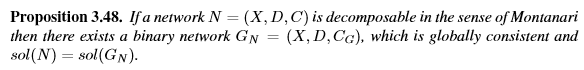
Montanari的可分解性强于通常所说的“可分解约束”。 （更多详细信息，请参见[63]或第3.8.2节。）示例3.47显示，不是因为网络是二进制的，它在Montanari意义上是可分解的。 对于二进制网络，Montanari提出了最小网络的概念，这是用于全局一致性的最佳近似二进制网络。 因此，这是收紧二进制网络的另一种技术。

定义3.49（Minimalnetwork） 给定二进制网络N =（X，D，C），N的最小网络是二进制归一化并且嵌入在D网络MN =（X，D，CM）中，使得长度2的任何本地一致的实例化是全局一致的并且sol （MN）= sol（N）。

推论3.50  给定二进制网络N，如果sol（N）在Montanari意义上是可分解的，则最小网络MN是全局一致的。

二进制网络上的极小性可以被认为是一种本地一致性。 但局部一致性通常指的是多项式强制执行的属性。 构建最小网络显然是难以处理的，因为一旦我们拥有最小网络，就可以确定原始网络的一致性（通过检查任何约束的空虚）。 建立最小网络的问题被蒙塔纳里称为“核心问题”。 这导致了一些混乱，因为有时候认为如果网络很小，生成解是多项式的。 Dechter通过以下方式部分地解决了歧义：

“然而，现在仍然不清楚是否生成单一最小网络解决方案很难，即使经验经验表明它通常很容易。 尽管如此，我们确实推测从最小网络生成单一解决方案很难......“

我们可以多说一点。

证明。 除非ΠP2=ΣP2 [29]，否则已知条款蕴涵问题是不可编译的。 在[38]中，Cros将子句蕴涵问题简化为二进制网络N中部分实例化的全局一致性问题的可编译性。如果在最小网络中构建解决方案是无回溯的，那么回答部分实例化是否全局一致将是多项式的。 此外，最小网络的大小为O（n2d2），这是N大小的多项式。因此，部分实例化的一致性问题是可编译的，并且条款蕴涵也是如此。

3.4.4 Consistencies Based on Constraints基于约束的一致性

到目前为止我研究的所有一致性（弧一致性除外）都是变量的部分实例化的特性。 它们没有考虑网络拓扑，即哪些变量集由约束链接而哪些不是。 这是约束传播的限制，它在网络中的任何地方创建新的约束。 如果我们想要在无回溯条件下链接一致性级别和超图结构，这也是对非二进制网络的限制。 在本节中，我将注意力限制在嵌入式网络中，因为我提出的所有工作都使用了此限制。

Janssenetal提出了基于变量的约束的第一个局部一致性[72]。 它适用于关系数据库的工作[7]。

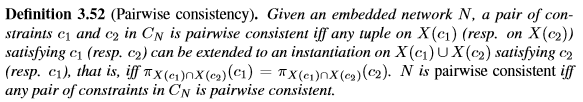
成对一致性：任取X(c1)的满足c1的元组，都可以扩展到X(c1) U X(c2)，满足c2。

Janssenetal在[72]中表明，在网络的双重编码中，对于2-一致性来说，它具有等效性，而且变量代表了原始网络的约束[48]。

在数据库环境中，Gyssens提出了k-一致性，成对一致性的直接扩展，我们一次考虑k个约束而不是两个[67]。 J'egou将这一概念应用于约束网络[73]。

k-一致性是k-逆一致性的基于约束的对应物（参见第3.5节）。 强制执行k-一致性不会改变相关的超图。 它只是改变现有的约束。 在[74]中，J'egoup提出了变量和约束之间的另一个二元性。 他呈现出超k一致性。 这是基于约束的k-一致性对应物。

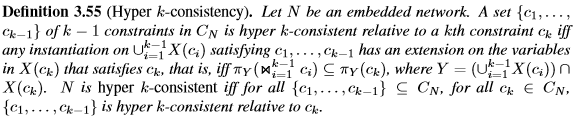
成对一致性是2向一致性和超2一致性。 根据定义3.55，J'egou描述了网络的一些充分条件是一致的。 这些条件将网络的超k一致性水平与其超图的宽度联系起来。 然而，超k-一致性继承了k-一致性的缺点之一，因为强制性一致性会增加新的约束，这些变量在原始网络中没有链接。 Dechter和van Beek提出了一种新的局部一致性形式，它与网络中已经存在的约束方案相比，超过了k-一致性。 他们将这些新的一致性称为关系一致性[49]。

设N是嵌入式网络。 CN中的约束c相对于变量Y subsetX（c）的子集是关系一致的，如果Y上的任何局部一致的实例化对X（c）上的元组的扩展满足c。 如果相对于X（c）的每个子集Y具有相对弧度一致，则c是关系弧一致的。 如果CN中的每个约束是关系一致的，则N是关系弧一致的。

关系弧一致性的一个优点是强制它不会在原始网络中未链接的变量之间创建约束。但是，它会在原始约束的方案的子集上创建子约束，这对于大型约束可能是禁止的，因为它最多可以为约束c创建2 | X（c）| 个子约束。

关系m-一致性具有与超k-一致性相同的缺点，因为它可以对m个约束之一中涉及的任何变量子集创建新约束。 Dechter和van Bee提出了关系m-一致性的有界版本，可以解决时空爆炸问题。

关系弧一致性对应于强关系（n，1） - 一致性和关系m-一致性对应于强关系（n，m） - 一致性。 广义弧一致性是关系（1,1）一致性。 关系（1，m） - 一致性是基于域的一致性，因此，不要修改约束集。

与强k-一致性的情况一样，强制关系（i，m）一致性的算法可以根据它们产生新约束的顺序收敛到不同的网络。

Dechter和van Beek提出了一种强制执行关系（i，m）一致性的算法。 它的复杂性在i·m中是指数级的。 他们还提出了一种自适应关系一致性算法。 它受到自适应一致性的启发（参见第7章），并应用适当级别的关系一致性来保证对给定变量排序的解决方案进行无回溯搜索。

沃尔什对关系一致性与k-一致性，k-逆一致性和广义弧一致性进行了广泛的理论比较[123]。