数据结构与算法之五——哈希表、堆

转(https://www.cnblogs.com/ysocean/p/8032660.html)

哈希表

• 哈希函数的引入：　

arrayIndex = largerNumber % smallRange

　　这也就是哈希函数。它把一个大范围的数字哈希（转化）成一个小范围的数字，这个小范围的数对应着数组的下标。使用哈希函数向数组插入数据后，这个数组就是哈希表。

• 冲突：把巨大的数字范围压缩到较小的数字范围，那么肯定会有几个不同的单词哈希化到同一个数组下标，即产生了冲突。

  • 当冲突产生时，一个方法是通过系统的方法找到数组的一个空位，并把这个单词填入，而不再用哈希函数得到数组的下标，这种方法称为开放地址法。比如加入单词 cats 哈希化的结果为5421，但是它的位置已经被单词parsnip占用了，那么我们会考虑将单词 cats 存放在parsnip后面的一个位置 5422 上。
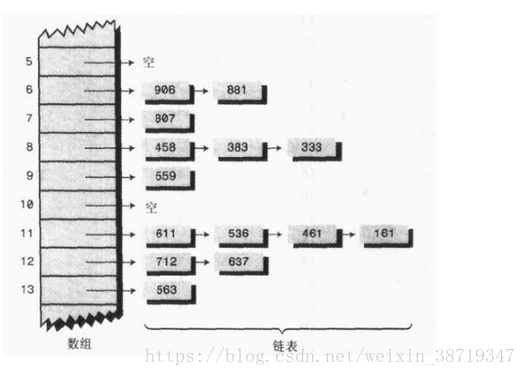
  • 　另一种方法，前面我们也提到过，就是数组的每个数据项都创建一个子链表或子数组，那么数组内不直接存放单词，当产生冲突时，新的数据项直接存放到这个数组下标表示的链表中，这种方法称为链地址法。

• 开放地址法
  ①、线性探测：在线性探测中，它会线性的查找空白单元。比如如果 5421 是要插入数据的位置，但是它已经被占用了，那么就使用5422，如果5422也被占用了，那么使用5423，以此类推，数组下标依次递增，直到找到空白的位置。这就叫做线性探测，因为它沿着数组下标一步一步顺序的查找空白单元。
  ②、二次探测：二测探测是防止聚集产生的一种方式，思想是探测相距较远的单元，而不是和原始位置相邻的单元。
  ③、再哈希法：方法是把关键字用不同的哈希函数再做一遍哈希化，用这个结果作为步长。对于指定的关键字，步长在整个探测中是不变的，不过不同的关键字使用不同的步长。

• 链地址法：在开放地址法中，通过再哈希法寻找一个空位解决冲突问题，另一个方法是在哈希表每个单元中设置链表（即链地址法），某个数据项的关键字值还是像通常一样映射到哈希表的单元，而数据项本身插入到这个单元的链表中。其他同样映射到这个位置的数据项只需要加到链表中，不需要在原始的数组中寻找空位。

• 找到初始单元需要O(1)的时间级别，而搜索链表的时间与M成正比，M为链表包含的平均项数，即O(M)的时间级别。

public LinkNode find(int key){
        int hashVal = hashFunction(key);
        LinkNode node = hashArray[hashVal].find(key);
        return node;
    }

• 总结 ：哈希表基于数组，类似于key-value的存储形式，关键字值通过哈希函数映射为数组的下标，如果一个关键字哈希化到已占用的数组单元，这种情况称为冲突。用来解决冲突的有两种方法：开放地址法和链地址法。在开发地址法中，把冲突的数据项放在数组的其它位置；在链地址法中，每个单元都包含一个链表，把所有映射到同一数组下标的数据项都插入到这个链表中。

堆

• 堆的引入：关于堆和优先级队列优先级队列是一种抽象数据类型（ADT），它提供了删除最大（或最小）关键字值的数据项的方法，插入数据项的方法，优先级队列可以用有序数组来实现，这种实现方式尽管删除最大数据项的时间复杂度为O(1)，但是插入还是需要较长的时间 O(N)，因为每次插入平均需要移动一半的数据项，来保证插入后，数组依旧有序。
• 注意这里的堆和我们Java语言，C++语言等编程语言在内存中的“堆”是不一样的，这里的堆是一种树，由它实现的优先级队列的插入和删除的时间复杂度都为O(logN)，这样尽管删除的时间变慢了，但是插入的时间快了很多，当速度非常重要，而且有很多插入操作时，可以选择用堆来实现优先级队列。
• 堆的定义：
  ①、它是完全二叉树，除了树的最后一层节点不需要是满的，其它的每一层从左到右都是满的。注意下面两种情况，第二种最后一层从左到右中间有断隔，那么也是不完全二叉树。
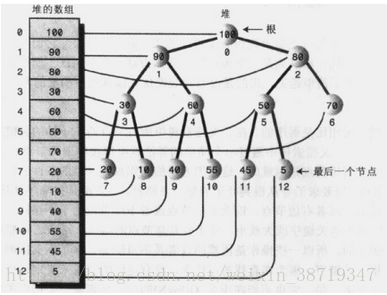
  ②、它通常用数组来实现。
  这种用数组实现的二叉树，假设节点的索引值为index，那么：

节点的左子节点是 2*index+1，

节点的右子节点是 2*index+2，

节点的父节点是 （index-1）/2。

③、堆中的每一个节点的关键字都大于（或等于）这个节点的子节点的关键字。
- 堆和前面说的二叉搜索树的区别：二叉搜索树中所有节点的左子节点关键字都小于右子节点关键字，在二叉搜索树中通过一个简单的算法就可以按序遍历节点。但是在堆中，按序遍历节点是很困难的，如上图所示，堆只有沿着从根节点到叶子节点的每一条路径是降序排列的，指定节点的左边节点或者右边节点，以及上层节点或者下层节点由于不在同一条路径上，他们的关键字可能比指定节点大或者小。所以相对于二叉搜索树，堆是弱序的。

• 遍历和查找：堆是弱序的，所以想要遍历堆是很困难的，基本上，堆是不支持遍历的。
  堆这种组织似乎非常接近无序，不过，对于快速的移除最大（或最小）节点，也就是根节点，以及能快速插入新的节点，这两个操作就足够了。

• 移除：移除是指删除关键字最大的节点（或最小），也就是根节点。

  　　根节点在数组中的索引总是0，即maxNode = heapArray[0];

  　　移除根节点之后，那树就空了一个根节点，也就是数组有了一个空的数据单元，这个空单元我们必须填上。

  　　第一种方法：将数组所有数据项都向前移动一个单元，这比较费时。

  　　第二种方法：

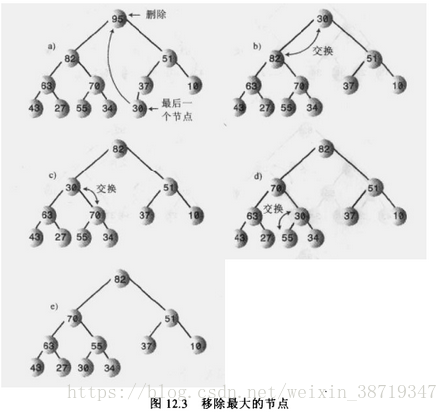
  　　　　①、移走根

  　　　　②、把最后一个节点移动到根的位置

  　　　　③、一直向下筛选这个节点，直到它在一个大于它的节点之下，小于它的节点之上为止。

  　　具体步骤如下：

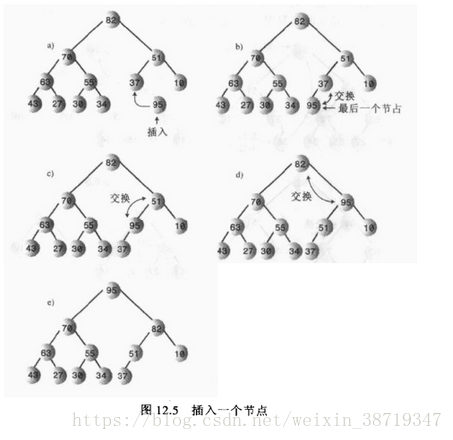
• 插入：插入节点也很容易，插入时，选择向上筛选，节点初始时插入到数组最后第一个空着的单元，数组容量大小增一。然后进行向上筛选的算法。

  　　注意：向上筛选和向下不同，向上筛选只用和一个父节点进行比较，比父节点小就停止筛选了。

• 完整的Java堆代码

public class Heap {

    private Node[] heapArray;
    private int maxSize;
    private int currentSize;

    public Heap(int mx) {
        maxSize = mx;
        currentSize = 0;
        heapArray = new Node[maxSize];
    }

    public boolean isEmpty() {
        return (currentSize == 0)? true : false;
    }

    public boolean isFull() {
        return (currentSize == maxSize)? true : false;
    }

    public boolean insert(int key) {
        if(isFull()) {
            return false;
        }
        Node newNode = new Node(key);
        heapArray[currentSize] = newNode;
        trickleUp(currentSize++);
        return true;
    }
    //向上调整
    public void trickleUp(int index) {
        int parent = (index - 1) / 2; //父节点的索引
        Node bottom = heapArray[index]; //将新加的尾节点存在bottom中
        while(index > 0 && heapArray[parent].getKey() < bottom.getKey()) {
            heapArray[index] = heapArray[parent];
            index = parent;
            parent = (parent - 1) / 2;
        }
        heapArray[index] = bottom;
    }

    public Node remove() {
        Node root = heapArray[0];
        heapArray[0] = heapArray[--currentSize];
        trickleDown(0);
        return root;
    }
    //向下调整
    public void trickleDown(int index) {
        Node top = heapArray[index];
        int largeChildIndex;
        while(index < currentSize/2) { //while node has at least one child
            int leftChildIndex = 2 * index + 1;
            int rightChildIndex = leftChildIndex + 1;
            //find larger child
            if(rightChildIndex < currentSize &&  //rightChild exists?
                    heapArray[leftChildIndex].getKey() < heapArray[rightChildIndex].getKey()) {
                largeChildIndex = rightChildIndex;
            }
            else {
                largeChildIndex = leftChildIndex;
            }
            if(top.getKey() >= heapArray[largeChildIndex].getKey()) {
                break;
            }
            heapArray[index] = heapArray[largeChildIndex];
            index = largeChildIndex;
        }
        heapArray[index] = top;
    }
    //根据索引改变堆中某个数据
    public boolean change(int index, int newValue) {
        if(index < 0 || index >= currentSize) {
            return false;
        }
        int oldValue = heapArray[index].getKey();
        heapArray[index].setKey(newValue);
        if(oldValue < newValue) {
            trickleUp(index);
        }
        else {
            trickleDown(index);
        }
        return true;
    }

    public void displayHeap() {
        System.out.println("heapArray(array format): ");
        for(int i = 0; i < currentSize; i++) {
            if(heapArray[i] != null) {
                System.out.print(heapArray[i].getKey() + " ");
            }
            else {
                System.out.print("--");
            }
        }
    }
}
class Node {
    private int iData;
    public Node(int key) {
        iData = key;
    }

    public int getKey() {
        return iData;
    }

    public void setKey(int key) {
        iData = key;
    }
}