数据降维PCA

自己实现

步骤

准备数据

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler

np.random.seed(42)
df = pd.read_csv('./data/pca.csv')
df

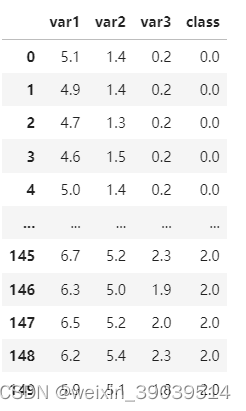
X = df.copy()
X
y = X.pop('class')
y

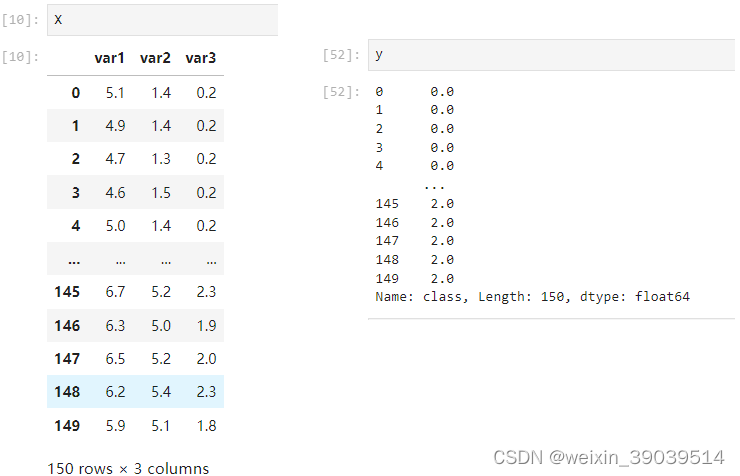
数据标准化

scaler = StandardScaler()
X_std = scaler.fit_transform(X)
X_std[:10]

array([[-0.90068117, -1.34022653, -1.3154443 ],
       [-1.14301691, -1.34022653, -1.3154443 ],
       [-1.38535265, -1.39706395, -1.3154443 ],
       [-1.50652052, -1.2833891 , -1.3154443 ],
       [-1.02184904, -1.34022653, -1.3154443 ],
       [-0.53717756, -1.16971425, -1.05217993],
       [-1.50652052, -1.34022653, -1.18381211],
       [-1.02184904, -1.2833891 , -1.3154443 ],
       [-1.74885626, -1.34022653, -1.3154443 ],
       [-1.14301691, -1.2833891 , -1.44707648]])

计算X_std的协方差矩阵

cov = np.cov(X_std, rowvar=False)
cov

array([[1.00671141, 0.87760447, 0.82343066],
       [0.87760447, 1.00671141, 0.96932762],
       [0.82343066, 0.96932762, 1.00671141]])

计算协方差矩阵的特征性向量和对应的特征值

eig_vals, eig_vecs = np.linalg.eig(cov)
(eig_vals, eig_vecs)

(array([2.78833033, 0.20075012, 0.03105378]),
 array([[ 0.55964149,  0.81270446,  0.16221241],
        [ 0.59148855, -0.2546058 , -0.76506024],
        [ 0.58046765, -0.52410624,  0.62319335]]))

按照特征值降序

eig_pairs = [
    (
        np.abs(eig_vals[i]),
        eig_vecs[:, i]
    )
    for i in range(len(eig_vals))
]
eig_pairs.sort(reverse=True)
eig_pairs

[(2.7883303296752913, array([0.55964149, 0.59148855, 0.58046765])),
 (0.20075011806343807, array([ 0.81270446, -0.2546058 , -0.52410624])),
 (0.031053780449189473, array([ 0.16221241, -0.76506024,  0.62319335]))]

取特征值最大的2个特征向量，创建参数矩阵W

W = np.hstack(
    (
        eig_pairs[0][1].reshape(3, 1),
        eig_pairs[1][1].reshape(3, 1),
    )
    
)
W

array([[ 0.55964149,  0.81270446],
       [ 0.59148855, -0.2546058 ],
       [ 0.58046765, -0.52410624]])

将X_std和W相乘，得到降维后的X_pca

X_pca = X_std.dot(W)
X_pca[:10]

array([[-2.06036006,  0.2986744 ],
       [-2.1959812 ,  0.10172707],
       [-2.36522102, -0.08074913],
       [-2.36579421, -0.20816508],
       [-2.12817063,  0.20020073],
       [-1.60325585,  0.4127035 ],
       [-2.32300467, -0.26268319],
       [-2.09455194,  0.1857296 ],
       [-2.53503403, -0.39064128],
       [-2.23877073,  0.15624518]])

sklearn PCA

scaler = StandardScaler()
X_std = scaler.fit_transform(X)
X_std[:10]

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
X_pca[:10]

data = df.values
scaler = StandardScaler()
data_std = scaler.fit_transform(data)
data_std

pca = PCA(n_components=3)
data_pca = pca.fit_transform(data_std)
data_pca.shape # (178, 3)
pca.explained_variance_ratio_ # array([0.33802319, 0.19967823, 0.13341533])
results = pd.DataFrame(
    data= {"variance_ratio": pca.explained_variance_ratio_}
)
results
results['cumulative'] = results['variance_ratio'].cumsum()
results['component'] = results.index + 1

results

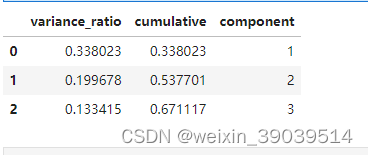
pca = PCA(n_components=0.95) # 95%特征
data_pca = pca.fit_transform(data_std)
pca.n_components_ # 8

PCA手写数字

from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

data = pd.read_csv(r".\digit recognizor.csv") 
X = data.iloc[:,1:]
y = data.iloc[:,0] 
X.shape #(42000, 784)

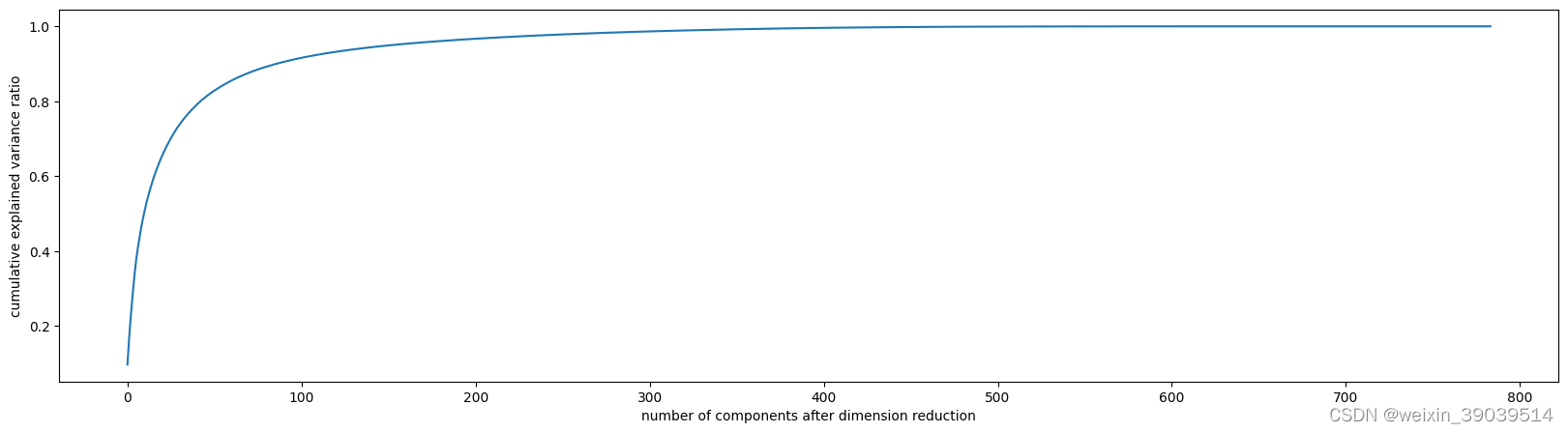
pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

#======【TIME WARNING：2mins 30s】======#
 
score = []
for i in range(1,101,10):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0)
                           ,X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()

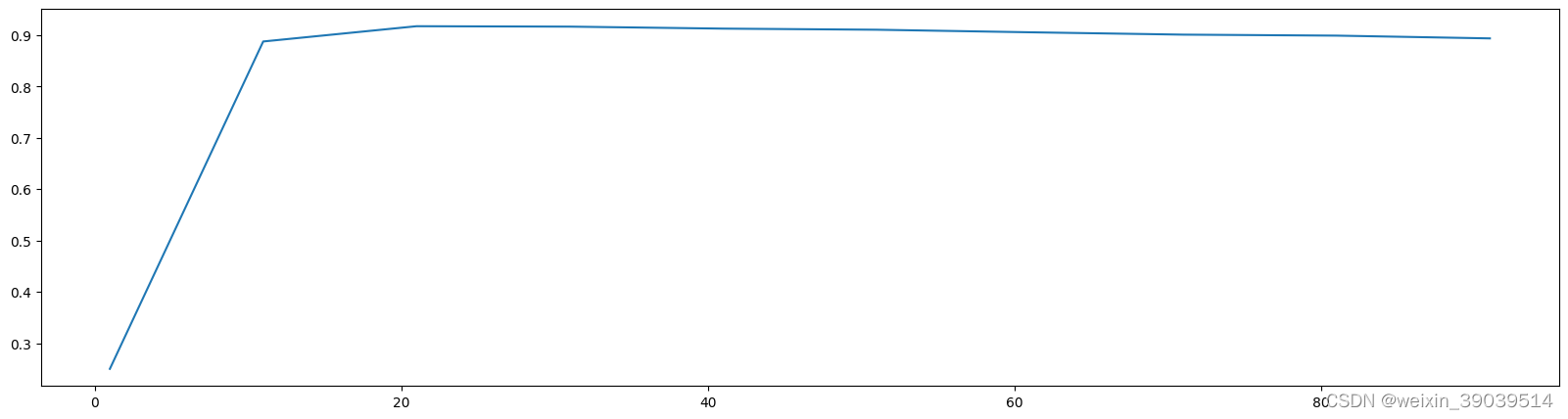
score = []
for i in range(10,25):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10,25),score)
plt.show()

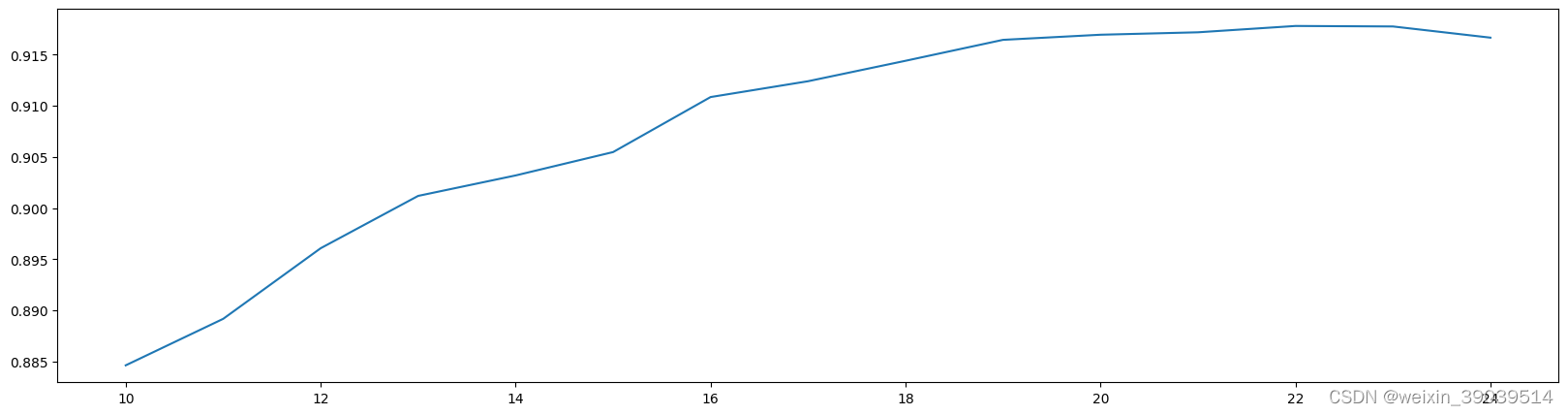
X_dr = PCA(22).fit_transform(X)
 
#======【TIME WARNING:1mins 30s】======#
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean() #0.946524472295366

from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(),X_dr,y,cv=5).mean()#KNN()的值不填写默认=5    0.9698566872605972

#======【TIME WARNING: 】======#

score = []
for i in range(10):
    X_dr = PCA(22).fit_transform(X)
    once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()

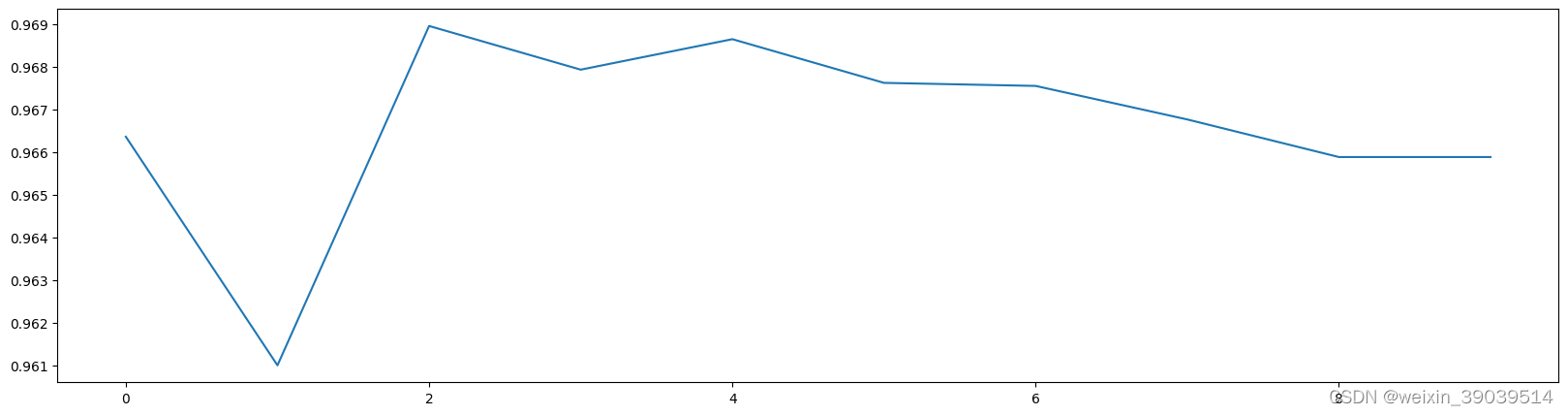
cross_val_score(KNN(4),X_dr,y,cv=5).mean()#KNN()的值不填写默认=5  # 0.968