几何画板200个经典课件_巧用“几何画板”探究一次函数的图象与性质

名称：《巧用“几何画板”探究一次函数的图象与性质》

作者：杨霞

单位：东莞市寮步宏伟初级中学

【问题的发现】

函数是初中阶段学生理解最难的一部分，也是学生开始学习变化关系的最重要的基础，如何让学生掌握好函数，变得十分重要，传统的教学模式只能通过老师手绘的函数图像来简单地认识函数的性质。我们的老师往往是通过列表、描点、连线画出图象，然后总结性质，这种方式会让学生显得枯燥无味，同时，函数的动态也没有体现出来，学生不能够很好的通过图象来理解函数的性质。

【问题的分析】

几何画板这个软件恰恰解决了这个问题，几何画板可以作出点、线、面、体、轨迹等，并且可以涂色来区别，让学生更加容易直观感受；几何画板还拥有变换功能——平移、旋转、缩放、反射等等，这些方便孩子进行观察图象，几何画板还具有动画功能，例如直线移动、转动、振动、曲线运动、轨迹追踪等等，这些可以帮助我们研究函数的变化趋势。最重要的是，它可以建立直角坐标系，方便我们作出线段、直线、一次函数图象、绘制点等等，让图象更加形象、直观。在时间上，几何画板的绘制函数图像功能可以帮助教师在很短的时间内画出想要的函数，也可以通过控制参数的大小，让学生观察函数的变化情况，充分发挥学生的主观能动性，共同总结出函数的性质和变化规律。尤其在初中一次函数教学中应用，会让我们的教学更加有效。所以在探究一次函数的图像与性质时，我决定尝试用《几何画板》。

【设计方案】

本次课将以“一次函数y=kx＋b（k、b是常数，k≠0）的图象与性质”这节课的设计为例，探究《几何画板》在研究函数图象与性质中的应用，特别是动态演示一次函数的图象与性质。

1、关于一次函数的图象

学生在学习一次函数的图象之前已经学习了函数的图象和正比例函数的图象，掌握了画函数图象的基本方法——描点法，因此，对于运用列表、描点、连线画出一次函数的近似图象并不生疏，但是对于一次函数的图象为一条直线的理解则是本节课的内容，所以，教学时需要在学生动手画图象的基础上，通过对一次函数与正比例函数解析式的分析比较，使学生从数的角度加深对形的理解．

2、关于一次函数的性质

对于一次函数的性质主要是研究一次函数中b的变化对一次函数图象的影响以及探究k的正负对函数增减性（图象的变化趋势）的影响。对于这两个性质的探究，让学生经历“先特殊化、简单化，再一般化、复杂化”的过程，通过对图象的研究和分析函数自身的性质,深刻领会函数解析式与函数图象之间的联系，渗透的是数形结合的思想．

（1）b的变化对一次函数图象的影响

操作步骤：首先在几何画板画出一次函数图象y=x+b，其中b=0,b=2,b=-2.分别是3条不一样颜色的直线。

将b=0改为b=2时，观察到紫色直线和红色直线重合了；

将b=0改为b=-2时，观察到紫色直线和蓝色直线重合了；通过改变b值，让学生观察动画，进而总结出一次函数的性质．

（2）探究k的正负对函数增减性（图象的变化趋势）的影响

操作步骤就是：首先在几何画板画出一次函数图象，然后通过改变k值，让学生观察动画，进而总结出一次函数的性质．

【行动实施】

一、条件

电脑、几何画板软件

二、资源准备

数学课堂，课件

三、操作方法

1、在数学课堂上做尝试，当讲解到一次函数的性质时，让学生进行小组合作探究，探究b的变化对于一次函数图象的影响.这时学生没有什么思路，都很苦恼，都听不懂。

2、这个时候由一位学霸同学进行操作演示，打开几何画板，展示出来三条函数图象；通过改变k值，观察图象的移动，边操作边讲解。这样动态演示一次函数的性质，非常直观，而且学生更加积极了，也加强了学生的理解。

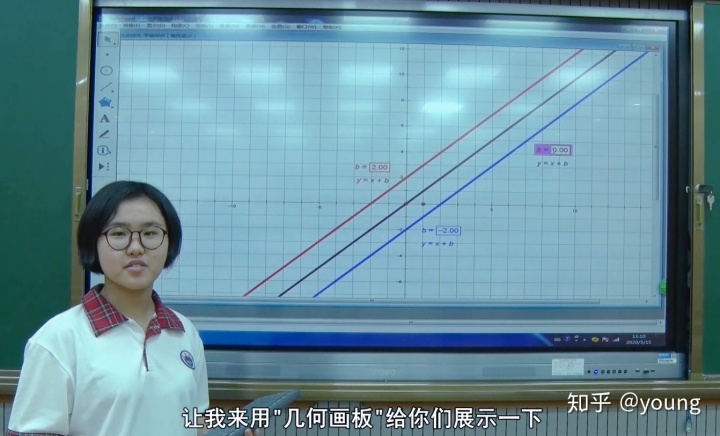
3、接着让学生也轮流上来操作几何画板，改变k值，进而加深理解

【总结反思】

在有关函数的教学实践中，初学的时候，通常学生都会感到一定的困难，我们教师常采用“数形结合”的数学思想帮助学生将抽象问题转化为形象问题。合理使用《几何画板》，就为“数形结合”思想的理解创造了一条便捷的通道，我们借助几何画板的动态性，使图形中各元素之间的位置关系和度量关系惟妙惟肖，使学生从各个不同的角度去观察图形，学生就会豁然开朗，学生在小组实验中发现规律、掌握性质，让学生获得的是真正的数学经验，而不仅仅是数学结论。

https://www.zhihu.com/video/1249420543516438528