c++杨辉三角_「知乎知识库」— 杨辉三角

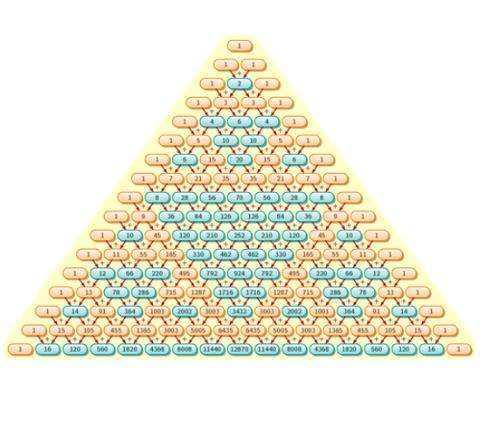
概述内容

杨辉三角是公元1261年，我国宋代数学家杨辉在其著作《详解九章算法》中给出的一个用数字排列起来的三角形阵。由于杨辉在书中引用了贾宪著的《开方作法本源》和“增乘开方法”，因此这个三角形也称“贾宪三角”。在欧洲，这个三角形叫帕斯卡三角形，是帕斯卡在1654年研究出来的，比杨辉晚了近400年时间。

发展历程

北宋人贾宪约1050年首先使用”贾宪三角”进行高次开方运算， 南宋数学家杨辉在《详解九章算法》（1261年）中，保存了一张宝贵图形——“开方作法本源”图。根据杨辉自注说，这个图“出《释锁算术》，贾宪用此术”。宋元时代的数学家求数字高次方程正根的方法叫做“开方“，又叫做“释锁”。很可能在杨辉之前，已经有一些数学家采用此图来研究开方术，其中以贾宪为最早。因此，我们应该把这个具有世界意义的重大贡献归功于贾宪和杨辉二人。贾宪采用得最早，但贾宪的著作可惜早已失传，全靠杨辉在《详解九章算法》里把这份珍贵的遗产保存了下来，并加以发扬光大，广泛应用。“开法作法本源” 图又叫做“乘方求廉图”，我们现在采取华罗庚教授的意见，称它为“杨辉三角”。

“开方作法本源”图

贾宪是天文学家楚衍的学生，他的履历我们知道的很少。他大概在宋仁宗时代（1023~1063年），就发现了二项高次幂（指数为正整数）展开式的各项系数的规律。在“杨辉三角”中，记录到五乘。

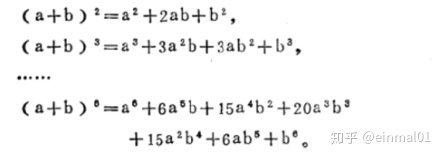
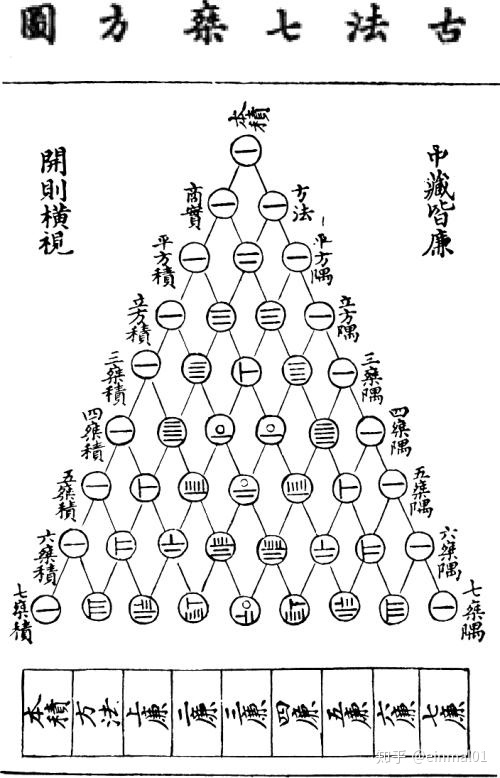
这是世界上最古老的记录。在杨辉之后，朱世杰在《四元玉鉴》中进一步发展为七乘，载有“古法七乘方图”，比原图多列两层，并且添上了几根斜线。他说这个三角形是古法，因为他至少比贾宪晚二百五十年。继朱世杰之后，明代数学家如吴敬、程大位等的著作中都有和“杨辉三角”相同的图形，可见我国历代数学家对这个图形都很重视。

古法七乘方图

“古法七乘方图”

在欧洲，称它为“巴斯加三角”。其实，在巴斯加之前，已经有不少人讨论过，其中最早的是德国人阿皮纳斯，他曾经把这张图形刻在1527年出版的一本算术书封面上。此后，德国人施蒂费尔（Stifel, 1544年），意大利人塔塔伊亚（Tartaglia,1550年）等都曾研究过这种图形。直到十七世纪，法国数学家帕斯卡在13岁时发现了“帕斯卡三角“。

杨辉三角的概述

我国当代数学家华罗庚教授在《从杨辉三角谈起》一书中，对它作过精彩的阐述与发挥。他把杨辉三角排列成下列现代形式，从图中我们很容易看出，这个三角的两条斜边都是由数字1组成的，而其余的数都等于它肩上的两个数相加。从图形上说明的任一数C(n,r)等于它肩上的两数C(n-1,r-1)及C(n-1,r)之和。写成数学关系式C(n,r)=C(n-1,r-1)+C(n-1,r)（n=1，2，3，···n）。

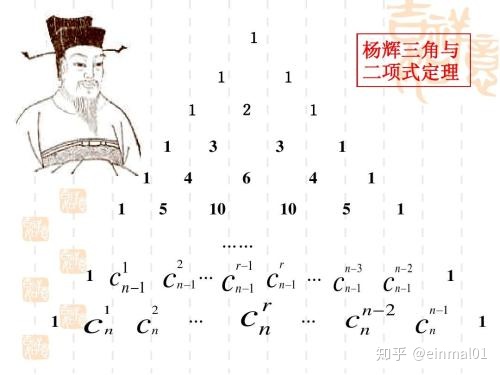
这个式子叫做杨辉恒等式，是杨辉三角的基本性质。杨辉每一行的数字左右对称，即C(n,r)=C(n,n-r)，由此可知，当n为奇数时，最中间的两个数最大，当n为偶数时，中间一个数最大。第n行的数字有n项，数字和为2的n-1次幂。(a+b)的n次方的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。杨辉三角的奇数行，即2的k次幂-1（k是正整数）行的各个数都是奇数，除2的k次幂行的所有数（两端的1除外）都是偶数。

将杨辉三角按如下图所示划出斜线，再求出斜线所经过的数字的和，1，1，2，3，5，8，13，21，···，此数列就是著名的斐波那契数列。这个数列最大特点就是其中每一项都等于其前两项的和。从第三个数起，每个数与它后面那个数的比值，都很接近于0.618，正是“黄金分割”。斐波那契数列又称“兔子数列”、黄金分割数列。这个看上去很简单的数列，却总是出现在人们的眼前。蜻蜓翅膀、蜂巢、菠萝表面的突起等，都是按照这个数列排列的。许多花朵的花瓣数目也具有斐波纳契数列的排列规律，如玫瑰、菊花、向日葵等。

杨辉三角中的斐波纳契数列

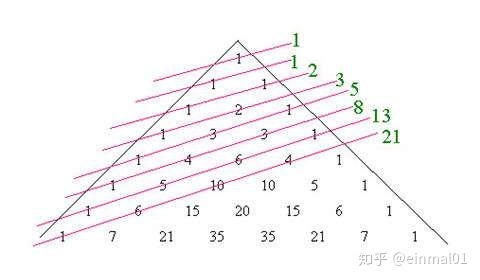
如果用笔将杨辉三角中的偶数与奇数分别标出，可以看到所有的偶数都会呈现出倒立的等边三角形状排列，而奇数都成正立的三角形排列，且等边三角形（偶数）的边长依次为：3，7，15，31，63，···，即所有的偶数依次排出以（2的n次幂-1）的长度为边长的倒立的等边三角形。

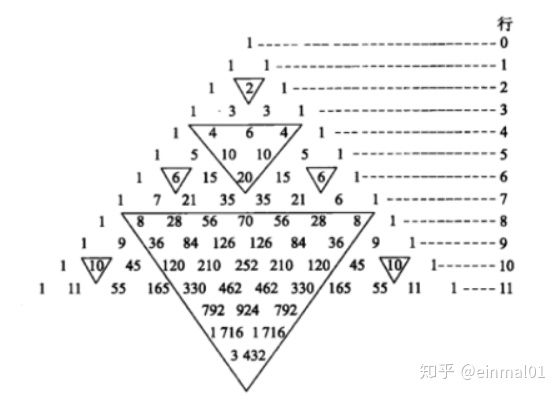
将所有等边三角形中的偶数去掉，剩下的图形是一个类似于分形几何中的谢尔宾斯基三角形，这种三角形是研究自然界大量存在的不规则现象（海岸线性状、大气运动、海洋湍流、野生生物群体涨落，乃至股市升降等）的崭新数学工具。

谢尔宾斯基三角形

杨辉三角的应用

利用杨辉三角的性质，我们可以把这一古代优秀创造发展推广到很多数学应用中去。例如，它可以直接联系到二项式定理，可用来作为开方的工具，发现高阶等差级数的计算规律，推导高次方程的计算方法，解释堆垛术、混合级数以及无穷级数的概念等，都可以与杨辉三角联系起来讨论。因此，直到现在，它仍然受到世界上数学家们的重视。例如，英国中学数学教科书中,也根据杨辉三角提出了几个有趣的问题。这些问题的讨论，对于丰富中学数学教学活动，是有着一定的价值的。

参考文献：

1. 吴效显, 赵赞. 杨辉三角形的推广[J]. 山东师范大学学报:自然科学版, 1994(2):122-123.
2. 黄俊峰, 袁方程. 自主探究教学的一个案例——自主探究“杨辉三角”与二项式系数[J]. 中小学数学(高中版), 2011(z1):13-15.
3. 刘天亮, 张利民. 杨辉三角形的若干性质[J]. 数学的实践与认识, 2007, 37(1):116-120.